Основные свойство транспортной задачи

Математические модели любых транспортных задач ЛП обладают общими чертами, а именно,

1) коэффициенты целевой функции неотрицательны (стоимости перевозок не могут быть отрицательными величинами);

2) коэффициенты правых частей ограничений неотрицательны (запасы и потребности продукта);

3) коэффициенты в ограничениях принимают только два значения, это нули и единицы.

В силу этих особенностей транспортная задача обладает следующими свойствами.

Теорема 1.

Базисное решение закрытой модели транспортной задачи содержит m+n-1 базисных компонент.

Доказательство.

Количество базисных компонент определяется число линейно независимых ограничений задачи. В транспортной задаче не все m+n ограничений линейно-независимы.

Действительно, сложив первые m ограничений и следующие n ограничений задачи, получим

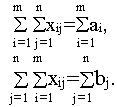
Но в закрытой модели выполняется балансовое равенство

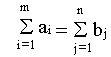
поэтому получаем, что нетривиальная линейная комбинация строк ограничений (линейная комбинация с ненулевыми коэффициентами) равна нулю. Это означает, что среди ограничений задачи есть линейно-зависимое ограничение. Следовательно, число линейно-независимых ограничений равно m+n-1 и базис задачи состоит из m+n-1 компонент.

Теорема доказана

В силу специфики содержательной постановки транспортной задачи допустимое решение называется планом, базисное допустимое решение называетсяопорным планом, оптимальное решение называется оптимальным планом.

Теорема 2.

Оптимальный план закрытой модели транспортной задачи существует всегда.

Доказательство.

Оптимальное решение задачи ЛП существует, если, во-первых, существует допустимое решение и, во-вторых, целевая функция ограничена на этом допустимом решении.

Покажем существование допустимого решения. Так как

суммарные запасы

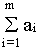
совпадают с суммарными потребностями

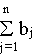
то всегда можно найти такой план перевозок, который будет допустимым решением (все запасы вывозятся и все потребности выполняются в силу балансового равенства).

Покажем ограниченность целевой функции.

Так как

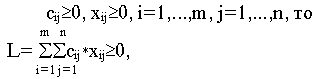
следовательно L ограничена снизу нулем для всех допустимых решений.

Теорема доказана

Двойственная задача

Запишем транспортную задачу в матричном виде

A- матрица ограничений, имеющая в соответствии с векторами х и b вид :

Двойственная задача к транспортной задаче в матричном виде будет иметь вид

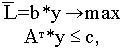
у- произвольного знака.

Распишем двойственную задачу в скалярном виде. Обозначим компоненты вектора

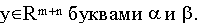
Тогда

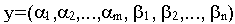
и ограничения двойственной задачи будут иметь вид :

или в общем виде двойственная задача

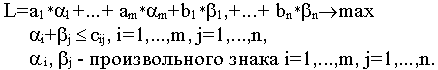
Двойственные переменные i, i=1,...,m, j, j=1,...,n, называются платежами, а

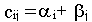
- псевдостоимость перевозок единицы груза из пункта i в пункт j, i=1,...,m, j=1,...,n.

Теоремы двойственности

ИЗ теории двойственности ЛП практический интерес представляет вторая теорема двойственности, из которой получается следующий критерий.