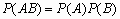Точки экстремума — это точки, в которых возрастание функции сменяется убыванием или наоборот. На графике они выглядят, как точки перегиба функции. Пик — это максимум, впадина — это минимум.
• Если точка является точкой экстремума функции f(x) и в этой точке существует производная , то она равна нулю.
• Если в точке производная меняет знак с плюса на минус, то точка является точкой максимума.
• Если в точке производная меняет знак с минуса на плюс, то точка является точкой минимума.
___________________________________________________________________________________________
1) (27490) 3) На рисунке изображен график функции y = f(x), определенной на интервале
( -2; 12). Найдите сумму точек экстремума функции f(x).
Экстремумы на графике выглядят как перегибы (пики и впадины). Точки экстремума - это значения x. На данном графике 7 экстремумов. Определим значения точек экстремума. (Считайте очень внимательно по клеточкам)
1; 2; 4; 7; 9;10;11
Теперь найдем их сумму: 1 + 2 + 4 + 7 + 9 + 10 + 11 = 44
Ответ: 44
2) (27494) На рисунке изображен график — производной функцииf(x), определенной на интервале (- 7; 14). Найдите количество точек максимума функции f(x), принадлежащих отрезку .
Обратите внимание, что здесь изображен не график функции, а графикпроизводной функции.
Точки максимума на данном графике - это точки, в которых производная меняет знак с плюса на минус. На отрезке производная меняет знак с плюса на минус только один раз - в точке x = 7. Так как нужно найти количество таких точек, то ответ равен 1.
Ответ: 1
19) Условия монотонности функции.
Теорема. 1) Если функция f(x) имеет производную на отрезке [a, b] и
возрастает на этом отрезке, то ее производная на этом отрезке
неотрицательна, т.е. f(x) 0.
2) Если функция f(x) непрерывна на отрезке [a, b] и
дифференцируема на промежутке (а, b), причем f(x) > 0 для a < x < b, то
эта функция возрастает на отрезке [a, b].
Аналогично можно сделать вывод о том, что если функция f(x) убывает
на отрезке [a, b], то f (x) 0 на этом отрезке. Если f (x) < 0 в промежутке
(a,b), то f(x) убывает на отрезке [a, b].
Конечно, данное утверждение справедливо, если функция f(x)
непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b).
Точки экстремума.
Точка x0 называется точкой минимума функции f(x), если можно
найти такую окрестность этой точки, что для любой точки x из этой
окрестности выполняется условие:
f(x) > f(x0).
Точка x0 называется точкой максимума функции f(x), если можно
найти такую окрестность этой точки, что для любой точки x из этой
окрестности выполняется условие:
f(x) < f(x0).
Точки максимума и минимума функции называются точками
экстремума.
Теорема. (необходимое условие существования экстремума) Если
функция f(x) дифференцируема в точке х = х1 и точка х1 является точкой
экстремума, то производная функции обращается в нуль в этой точке.
Точки, где f (x) 0 называются стационарными точками, или
точками возможного экстремума.
Отсюда следует, что точки экстремума функции следует искать среди
тех точек её области определения, где производная функции равна нулю или
не существует.
Точки области определения функции, в которых производная либо
равна нулю, либо не существует, называются критическими.
Теорема. (Достаточные условия существования экстремума)
Пусть функция f(x) непрерывна в интервале (a, b), который содержит
критическую точку х1, и дифференцируема во всех точках этого интервала
(кроме, может быть, самой точки х1).
Если при переходе через точку х1 слева направо производная функции
f(x) меняет знак с “+” на “-“, то в точке х = х1 функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет
минимум.
Исследование функции на экстремум с помощью
производных высших порядков.
Пусть в точке х = х1 f(x1) = 0 и f(x1) существует и непрерывна в
некоторой окрестности точки х1.
Теорема. Если f(x1) = 0, то функция f(x) в точке х = х1 имеет
максимум, если f(x1)<0 и минимум, если f(x1)>0.
Выпуклость и вогнутость кривой.
Точки перегиба.
Кривая обращена выпуклостью вверх на интервале (а, b), если все ее
точки лежат ниже любой ее касательной на этом интервале. Кривая,
обращенная выпуклостью вверх, называется выпуклой, а кривая,
обращенная выпуклостью вниз – называется вогнутой.
Теорема. Если функция y=f(x) имеет на интервале (a, b) вторую
производную и f (x) 0( f (x) 0) во всех точках интервала (a, b), то график
функции имеет выпуклость, направленную вниз (вверх).
Точка x0 называется точкой перегиба функции f(x), если в этой точке
функция имеет производную и существуют два промежутка: (a;x0) и (x0;b), на
одном из которых функция выпукла, а на другом вогнута. Угловая точка не
является точкой перегиба.
Теорема. Пусть кривая определяется уравнением y = f(x). Если вторая
производная f(a) = 0 или f(a) не существует и при переходе через точку
х = а f(x) меняет знак, то точка кривой с абсциссой х = а является точкой
перегиба.
20) Первообра́зной[1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Так, например, функция 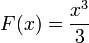 является первообразной
является первообразной 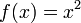 . Так как производная константы равна нулю,
. Так как производная константы равна нулю,  будет иметь бесконечное количество первообразных, таких как
будет иметь бесконечное количество первообразных, таких как 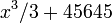 или
или 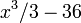 … и т. д.; таким образом семейство первообразных функции
… и т. д.; таким образом семейство первообразных функции 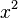 можно обозначить как
можно обозначить как 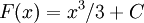 , где C — любое число.Графики
, где C — любое число.Графики
Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:
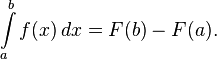
Это соотношение называется формулой Ньютона — Лейбница.
Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f и записывают в виде интеграла без указания пределов:
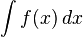
Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.
Каждая непрерывная функция f имеет первообразную F, одна из которых представляется в виде интеграла от f с переменным верхним пределом:
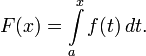
Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например, 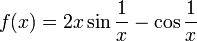 с
с 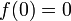 не непрерывна при
не непрерывна при 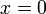 , но имеет первообразную
, но имеет первообразную 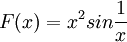 с
с 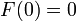 .
.
Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (такие как многочлены, экспоненциальные функции,логарифмы
, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например: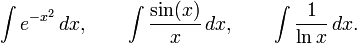
Неопределённый интегра́л для функции 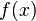 — это совокупность всех первообразных данной функции.
— это совокупность всех первообразных данной функции.
Если функция 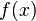 определена и непрерывна на промежутке
определена и непрерывна на промежутке 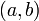 и
и 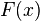 — её первообразная, то есть
— её первообразная, то есть 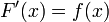 при
при 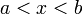 , то
, то
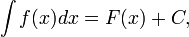
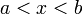 ,
,
где С — произвольная постоянная.
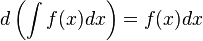
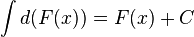
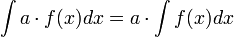
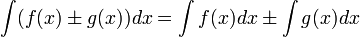
Если 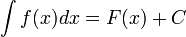 , то и
, то и 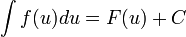 , где
, где 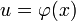 — произвольная функция, имеющая непрерывную производную
— произвольная функция, имеющая непрерывную производную
Основные свойства
1. 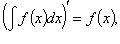
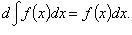
2. 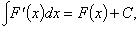
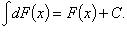
3. Если 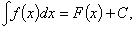 то
то
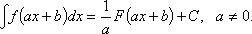
4. 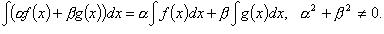
21) Одним из главных способов преобразования неопределенных интегралов к табличным является метод замены переменной. Он имеет два варианта. Первый вариант используется после подведения под знак дифференциала, когда имеется равенство
| ∫ U(x) · V'(x) dx = ∫ U(x) dV(x) . |
Если функция U(x) выражается через функцию V(x) по некоторой формуле U(x) = w(V(x)), то
| ∫ U(x) dV(x) = ∫ w(V(x)) dV(x) = ∫ w(t) dt |
где t = V(x). Таким образом отыскание исходного интеграла сводится к отысканию интеграла
∫ w(t) dt
В нем функция t = V(x) выступает как независимая переменная, т.е. произошла замена переменной. Новая переменная t вводится как функция исходной переменной x. Не требуется, чтобы соответствие между x и t было взаимно однозначным.
Во втором варианте метода замены переменной новая переменная t вводится равенством x = (t). Функция (t) называется подстановкой. Она взаимно однозначна, т.е. имеет обратную. Этот метод основывается на следующей теореме.
Теорема. Пусть существует неопределенный интеграл
| ∫ f(x) dx |
и пусть x = (t) , где (t) — непрерывно дифференцируемая функция, имеющая обратную функцию t = − 1(x) .
Тогда
| ∫ f(x) dx = ∫ f((t)) · '(t) dt при t = − 1(x). | (1) |
Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 167.
Подобрать нужную подстановку x = (t) — искусство интегрирования. Иногда на ум приходит сначала не x = (t), а обратная функция t = − 1(x) . Часто приходится испробовать несколько подстановок, прежде чем будет найдена та, с помощью которой данный интеграл сводится к табличному. Некоторые подстановки оказались столь удачными, что им присвоены специальные названия. Например, используются подстановки Абеля, Эйлера, гиперболические, дробно–линейные, тригонометрические и др. Некоторые интегралы разными подстановками сводятся к разным табличным интегралам.
Метод интегрирования по частям позволяет свести исходный неопределенный интеграл к более простому виду либо к табличному интегралу. Этот метод наиболее часто применяется, если подынтегральная функция содержит логарифмические, показательные, обратные тригонометрические, тригонометрические функции, а также их комбинации.
Формула интегрирования по частям следующая 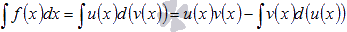 .
.
То есть, подынтегральное выражение f(x)dx представляем в виде произведения функции u(x)на d(v(x)) - дифференциал функции v(x). Далее находим функцию v(x) (чаще всего методом непосредственного интегрирования) и d(u(x)) - дифференциал функции u(x). Подставляем найденные выражения в формулу интегрирования по частям и исходный неопределенный интеграл сводится к разности 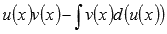 . Последний неопределенный интеграл может быть взят с использованием любого метода интегрирования, в том числе и метода интегрирования по частям.
. Последний неопределенный интеграл может быть взят с использованием любого метода интегрирования, в том числе и метода интегрирования по частям.
В качестве примера найдем множество первообразных функции логарифма.
Пример.
Найти неопределенный интеграл 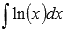
Решение.
Найдем этот неопределенный интеграл методом интегрирования по частям. В качестве функции u(x) возьмем ln(x), а в качестве d(v(x)) оставшуюся часть подынтегрального выражения, то есть dx.
Имеем, 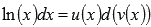 , где
, где 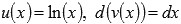 .
.
Дифференциал функции u(x) есть 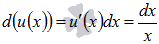 , а функция v(x) – это
, а функция v(x) – это 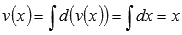 .
.
ЗАМЕЧАНИЕ: константу С при нахождении функции v(x) считают равной нулю.
Теперь все подставляем в формулу интегрирования по частям:
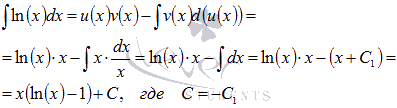
Ответ:
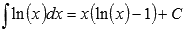 .
.
Определение
Пусть 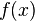 определена на
определена на 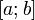 . Разобьём
. Разобьём 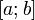 на части с несколькими произвольными точками
на части с несколькими произвольными точками 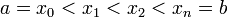 . Тогда говорят, что произведено разбиение
. Тогда говорят, что произведено разбиение 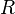 отрезка
отрезка 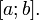 Далее выберем произвольную точку
Далее выберем произвольную точку 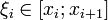 ,
, 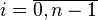 ,
,
Определённым интегралом от функции 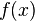 на отрезке
на отрезке 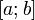 называется предел интегральных сумм при стремлении ранга разбиения к нулю
называется предел интегральных сумм при стремлении ранга разбиения к нулю 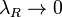 , если он существует независимо от разбиения
, если он существует независимо от разбиения 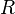 и выбора точек
и выбора точек 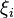 , то есть
, то есть
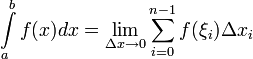
Если существует указанный предел, то функция 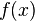 называется интегрируемой на
называется интегрируемой на 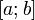 по Риману.
по Риману.
[править]Обозначения
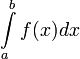
· 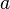 — нижний предел.
— нижний предел.
· 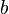 — верхний предел.
— верхний предел.
· 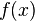 — подынтегральная функция.
— подынтегральная функция.
· 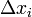 — длина частичного отрезка.
— длина частичного отрезка.
· 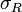 — интегральная сумма от функции
— интегральная сумма от функции 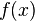 на
на 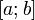 соответствующей разбиению
соответствующей разбиению 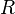 .
.
· 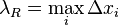 — максимальная длина част. отрезка.
— максимальная длина част. отрезка.
[править]Свойства
Если функция 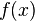 интегрируема по Риману на
интегрируема по Риману на 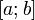 , то она ограничена на нем.
, то она ограничена на нем.
[править]Геометрический смысл


Определённый интеграл как площадь фигуры
Определённый интеграл 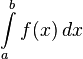 численно равен площади фигуры, ограниченной осью абсцисс, прямыми
численно равен площади фигуры, ограниченной осью абсцисс, прямыми  и
и 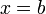 и графиком функции
и графиком функции 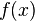
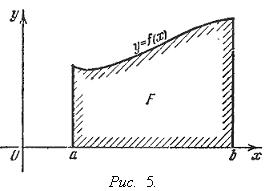
Геометрический смысл определенного интеграла. Если f(x) непрерывна и положительна на [a, b], то интеграл
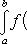
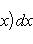
представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x) (см. рис. 5.).
Не следует думать, что условие непрерывности функции необходимо для того, чтобы у нее существовал определенный интеграл. Интеграл может существовать и у разрывной функции. Пусть, например, функция f(x), заданная на промежутке [a, b], равна нулю во всех точках этого промежутка, кроме конечного числа точек z1, z2, ..., zN. Составим для f(x) интегральную сумму σ.
Пусть из точек ξ0, ξ1, ..., ξn-1, входящих в определение σ, p точек совпадают с точками zi, а остальные отличны от них. Тогда в сумме σ будет лишь p слагаемых, отличных от нуля. Если наибольшее из чисел | f(zi) | (i = 1, 2, ..., N) есть K, то, очевидно,
| σ | ≤ Kpλ ≤ KNλ,
откуда ясно, что при λ → 0 будет и σ → 0. Таким образом, интеграл
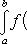
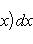
существует и равен нулю.
Приведем теперь пример функции, не имеющей интеграла. Пусть φ(x) задана на промежутке [0, 1] так:
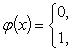
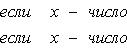
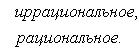
Если мы, составляя сумму σ, за точки ξk выберем числа иррациональные, то окажется σ = 0. Если же все ξk взять рациональными, то получится σ = 1. Таким образом, за счет одного лишь уменьшения λ нельзя приблизить σ к какому-либо постоянному числу, и интеграл
не существует.
В настоящее время известны точные признаки, позволяющие судить, имеет или нет заданная функция определенный интеграл, но мы ограничимся вышеприведенной теоремой об интегрируемости непрерывных функций.
23) I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. 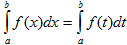 , где х, t – любые буквы.
, где х, t – любые буквы.
II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
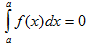
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
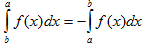
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
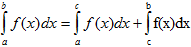
V. Постоянный множитель можно выносить за знак определенного интеграла.
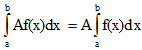
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
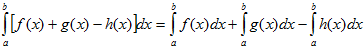
Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.
Если  непрерывна на отрезке непрерывна на отрезке  и и 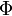 — ее любая первообразная на этом отрезке, то имеет место равенство — ее любая первообразная на этом отрезке, то имеет место равенство 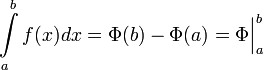 |
24) Случайные события.
Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти. Например если брошена монет она может упасть вверх гербом или вверх надписью. Поэтому событие ?при бросании монеты выпал герб? - случайное. Каждое случайное событие , в частности выпадение герба, есть следствие действия многих случайных причин (сила с которой брошена монета, форма монеты, вес и т.д.). Не возможно учесть влияние этих причин на результат, по сколку их число очень велико, по этому теория вероятностей не ставит перед собой задачу предсказать. Произойдет единичное событие или нет.
В дальнейшем, вместо того чтобы говорить ?совокупность условий S осуществлена?, будем говорить кратко ?произведено испытание?. Таким образом, события будет рассматривается как результат испытания.
2.2.Классификация случайных событий.
Полной группой событий называются несколько событий таких что в результате опыта непременно должно произойти хотя бы одно из них.
События называют несовместными, если появление одного из них исключает появления других событий в одном и том же испытании.
События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.
Вероятность события. Классическое определение вероятности
Пусть = { 1, 2, …, s} - произвольное конечное пространство элементарных событий, A - событие, состоящее из k элементарных событий: A={ i1, i2, …, ik}, 1 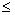 i1
i1 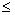 i2
i2 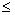 …
… 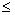 i k
i k 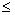 s, k = 1, 2,…, s, и пусть
s, k = 1, 2,…, s, и пусть 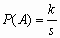 . Определенная таким образом функция P(A) удовлетворяет всем аксиомам 1-4(здесь множество
. Определенная таким образом функция P(A) удовлетворяет всем аксиомам 1-4(здесь множество 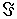 состоит из всех подмножеств множества :
состоит из всех подмножеств множества : 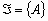 ). Таково классическое определение вероятности события A.
). Таково классическое определение вероятности события A.
Принята следующая формулировка классического определения вероятности: вероятностью события A называется отношение числа исходов, благоприятствующих A, к общему числу исходов.
Из приведенных определений следует: P( 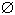 )=0,
)=0, 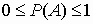 ,
, 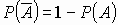 .
.
Вероятность суммы событий
Для любых двух событий A и B справедливо: 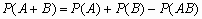 .
.
Если события A и B несовместны, то 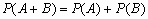 .
.
Вероятность произведения событий. Условная вероятность. Независимые события
Условная вероятность P(A/B) события A при условии, что событие B произошло, P(B) > 0, определяется формулой
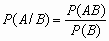 .
.
Для любых двух событий A и B справедливо: 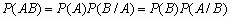 .
.
События A и B называются независимыми, если 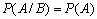 . Для любых двухнезависимых, событий A и B справедливо:
. Для любых двухнезависимых, событий A и B справедливо: