Уравнение линии на плоскости
Определение. Уравнением линии (кривой) на плоскости называется уравнение, которому удовлетворяют координаты и каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
 Если точка передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты называются текущими координатами.
Если точка передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты называются текущими координатами.
Любую линию в принципе можно выразить соответствующим уравнением. Однако не всякое уравнение на определяет на плоскости некоторую линию.
Например: определяет только одну точку (0;0);
не определяет никакого множества точек, т.к. левая часть уравнения не может равняться нулю.
Чтобы убедится, лежит ли точка на данной линии , надо проверить, удовлетворяют ли координаты этой точки уравнению.
Уравнения линии могут быть самыми различными, однако надо отметить, что не каждое уравнение имеет геометрический образ в виде линии.
Взаимное расположение двух линий
Чтобы определить взаимное расположение 2-х линий, необходимо знать уравнений этих линий. Если система этих уравнений совместна, то линии имеют общие точки. В противном случае общих точек нет. Число общих точек равно числу решений системы уравнений
Например, прямая линия и окружность 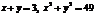 имеют 2 общие точки, так как система из этих уравнений имеет два решения:
имеют 2 общие точки, так как система из этих уравнений имеет два решения:
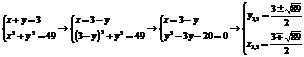 .
.
Уравнение прямой на плоскости
В декартовой системе координат рассмотрим прямую 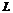 , расположенную под углом
, расположенную под углом 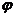 к оси
к оси 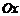 (рис. 3.7).
(рис. 3.7).
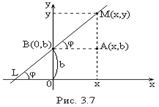 | Выберем на прямой L произвольную точку 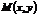 . Из . Из 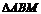 найдем тангенс угла наклона прямой: найдем тангенс угла наклона прямой: 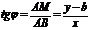 . Введем угловой коэффициент прямой . Введем угловой коэффициент прямой 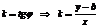 . Из последнего равенства . Из последнего равенства 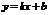 (3.1) (3.1) |
Полученное уравнение называется уравнением прямой с угловым коэффициентом.
Частные случаи уравнения (3.1):
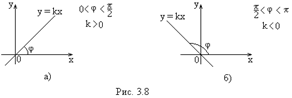
1) Если 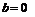 , тогда
, тогда 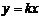 и уравнение (3.1) представляет прямую, проходящую через начало координат под углом
и уравнение (3.1) представляет прямую, проходящую через начало координат под углом 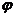 к оси
к оси 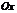 (рис. 3.8).
(рис. 3.8).

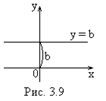
2) Если 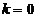 (т.е.
(т.е. 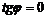 ), тогда
), тогда 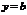 и уравнение (3.1) представляет собой прямую, параллельную оси
и уравнение (3.1) представляет собой прямую, параллельную оси 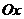 (рис. 3.9).
(рис. 3.9).

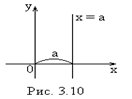
3)Если 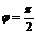 , тогда прямая
, тогда прямая  (рис. 3.10). Предположим, что
(рис. 3.10). Предположим, что 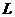 отсекает на оси
отсекает на оси 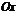 отрезок, равный
отрезок, равный 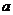 (рис. 3.10). Очевидно, что уравнений такой прямой
(рис. 3.10). Очевидно, что уравнений такой прямой 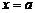 .
.
Уравнение прямой, проходящей через заданную точку в данном направлении
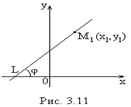 | Пусть прямая  образует с осью образует с осью  угол угол  и проходит через точку и проходит через точку 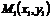 . Т.к. . Т.к. 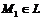 , то ее координаты удовлетворяют уравнению (3.1), т.е. , то ее координаты удовлетворяют уравнению (3.1), т.е. 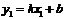 . (3.2) Вычитая из (3.1) уравнение (3.2), получим . (3.2) Вычитая из (3.1) уравнение (3.2), получим 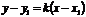 . (3.3) Полученное уравнение называется уравнением прямой по точке и угловому коэффициенту . (3.3) Полученное уравнение называется уравнением прямой по точке и угловому коэффициенту 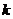 . . |
Уравнение прямой, проходящей через две заданные точки
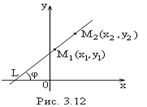 | Пусть известны две точки, принадлежащие 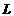 , , 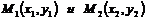 . Запишем уравнение прямой по точке . Запишем уравнение прямой по точке 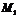 и угловому коэффициенту и угловому коэффициенту 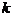 : : 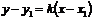 . (3.4) Т.к. точка . (3.4) Т.к. точка 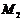 также принадлежит также принадлежит 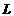 , то ее координаты будут удовлетворять данное равенство: , то ее координаты будут удовлетворять данное равенство: 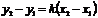 . . |
Из последнего равенства 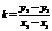 . Подставляя выражение для
. Подставляя выражение для 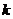 в уравнение (3.4):
в уравнение (3.4): 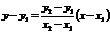 , получим уравнение прямой по двум точкам
, получим уравнение прямой по двум точкам
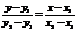 (3.5).
(3.5).
Уравнение пучка прямых
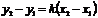
Уравнение прямой в отрезках
Уравнение называется уравнением прямой в отрезках.
