Найдем решение предыдущей системы уравнений методом Гаусса – Зейделя.

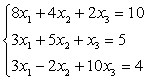
Расчетные формулы:

k	x1	x2	x3	точность
	1.250	0.250	0.075	1.2500
	1.106	0.321	0.132	0.1438
	1.056	0.340	0.151	0.0500
	1.042	0.344	0.156	0.0139
	1.039	0.346	0.157	0.0036

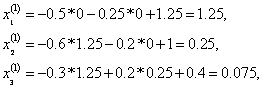
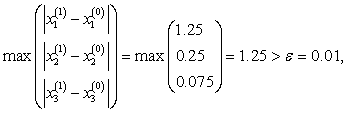
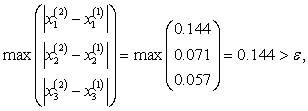
Из таблицы видно, что нужная точность достигнута уже на 5–ой итерации вместо 13–ой по методу простой итерации и значения корней более близки к значениям, полученным методом обратной матрицы.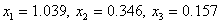

Элементы функционального анализа

1.А) Понятие функциональной зависимости

Будем говорить, что между двумя признаками X и Y существует функциональная зависимость (взаимосвязь), при которой каждому значению одного из них соответствует одно или несколько строго определенных значений другого.

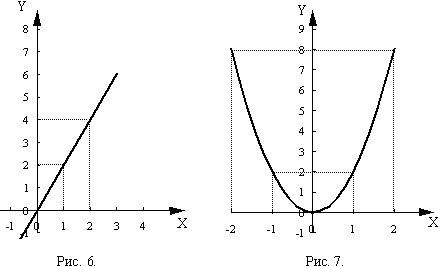
Например, в функции у = 2 * х каждому значению х соответствует в два раза большее значение у . В функции 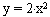каждому значению у соответствует 2 определенных значения х . Графически это выглядит так (рис. 6, 7 соответственно):

Б)!!!!!!!!????

2)???????

Векторная алгебра.

1. Векторные и скалярные величины.

 Вектор − чисто математическое понятие, которое лишь применяется в физике или других прикладных науках и которое позволяет упростить решение некоторых сложных задач.
 Вектор − направленный отрезок прямой.
В курсе элементарной физики приходится оперировать двумя категориями величин −  скалярными и векторными.
 Скалярными величинами (скалярами) называют величины, характеризующиеся числовым значением и знаком. Скалярами являются длина − l, масса − m, путь − s, время − t, температура − T, электрический заряд − q, энергия − W, координаты и т.д.
К скалярным величинам применяются все алгебраические действия (сложение, вычитание, умножение и т.д.). 

 Пример 1.
Определить полный заряд системы, состоящий из зарядов, входящих в нее, если q ₁ = 2 нКл, q₂ = −7 нКл, q₃ = 3 нКл.
Полный заряд системы

q = q₁ + q₂ + q₃ = (2 − 7 + 3) нКл = −2 нКл = −2 × 10⁻⁹ Кл.

 Пример 2.
Для квадратного уравнения вида 

ax² + bx + с = 0;

x_1,2 = (1/(2a)) × (−b ± √{b² − 4ac}).

 Векторными величинами (векторами) называют величины, для определения которых необходимо указать кроме численного значения так же и направление. Векторы − скорость v, сила F, импульс p, напряженность электрического поля E, магнитная индукция B и др.
Численное значение вектора (модуль) обозначают буквой без символа вектора или заключают вектор между вертикальными черточками  r = |r|.
Графически вектор изображают стрелкой (рис. 1), 

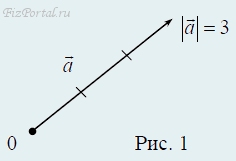
длина которой в заданном масштабе равна его модулю, а направление совпадает с направлением вектора.
Два вектора равны, если совпадают их модули и направления.
Векторные величины складываются геометрически (по правилу векторной алгебры). 
Нахождение векторной суммы по данным составляющим векторам называется сложением векторов. 
Сложение двух векторов производят по правилу параллелограмма или треугольника. Суммарный вектор 

с = a + b

равен диагонали параллелограмма, построенного на векторах a и b. Модуль его

с = √{a² + b² − 2abcosα} (рис. 2).

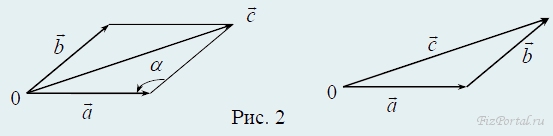
При α = 90°, с = √{a² + b²} − теорема Пифагора.

Тот же вектор c можно получить по правилу треугольника, если из конца вектора  a отложить вектор b. Замыкающий вектор c (соединяющий начало вектора a и конец вектора b) является векторной суммой слагаемых (составляющих векторов a и b).
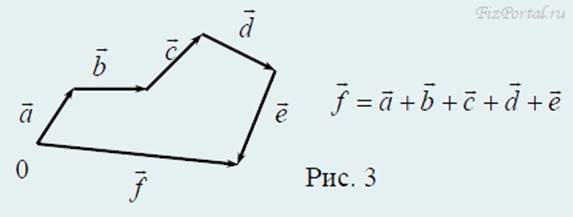
Результирующий вектор находят как замыкающую той ломанной линии, звеньями которой являются составляющие векторы (рис. 3). 

 Пример 3.
Сложить две силы F ₁ = 3 Н и F₂ = 4 Н, векторы F₁ и F₂ составляют с горизонтом углы α₁ = 10° и α₂ = 40°, соответственно
 F = F₁ + F₂ (рис. 4).

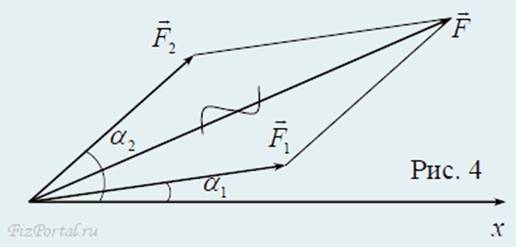
Результатом сложения этих двух сил является сила, называемая равнодействующей. Вектор  F направлен по диагонали параллелограмма, построенного на векторах F₁ и F₂, как сторонах, и по модулю равен ее длине.
Модуль вектора  F находим по теореме косинусов

F = √{F₁² + F₂² + 2F₁F₂cos(α₂ − α₁)},

F = √{3² + 4² + 2 × 3 × 4 × cos(40° − 10°)} ≈ 6,8 H.

Если

(α₂ − α₁) = 90°, то F = √{F₁² + F₂²}.

Угол, который вектор  F составляет с осью Ox, находим по формуле

α = arctg((F₁sinα₁ + F₂sinα₂)/(F₁cosα₁ + F₂cosα₂)),

α = arctg((3•0,17 + 4•0,64)/(3•0,98 + 4•0,77)) = arctg0,51, α ≈ 0,47 рад.

Проекция вектора a на ось Ox (Oy) − скалярная величина, зависящая от угла α между направлением вектора  a и оси Ox (Oy). (рис. 5)

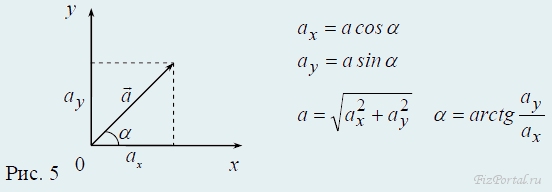
Проекции вектора  a на оси Ox и Oy прямоугольной системы координат. (рис. 6)

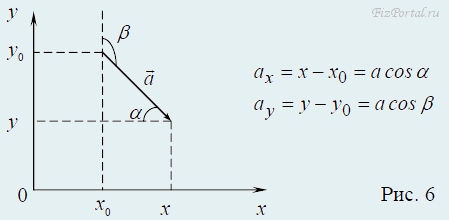
Чтобы не допустить ошибок при определении знака проекции вектора на  ось, полезно запомнить следующее правило: если направление составляющей совпадает с направлением оси, то проекция вектора на эту ось положительна, если же направление составляющей противоположно направлению оси, то проекция вектора отрицательна. (рис. 7)

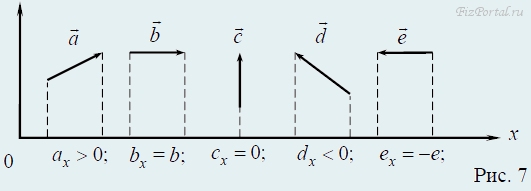
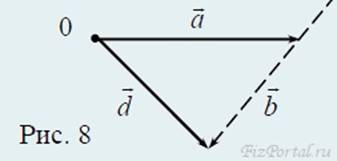
Вычитание векторов − это сложение, при котором к первому вектору  прибавляется вектор, численно равный второму, противоположно направленный

a − b = a + (−b) = d (рис. 8).

Пусть надо из вектора  a вычесть вектор b, их разность − d. Чтобы найти разность двух векторов, надо к вектору a прибавить вектор (−b), то есть вектором d = a − b будет вектор, направленный от начала вектора a к концу вектора (−b) (рис. 9).

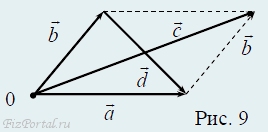
В параллелограмме, построенном на векторах  a и b как сторонах, одна диагональ c имеет смысл суммы, а другая d − разности векторов a и b (рис. 9).
Произведение вектора  a на скаляр k равно вектору b = ka, модуль которого в k раз больше модуля вектора a, а направление совпадает с направлением a при положительном k и противоположно ему при отрицательном k.

 Пример 4.
Определить импульс тела массой 2 кг, движущегося со скоростью 5 м/с. (рис. 10) 

Импульс тела p = mv; p = 2 кг•м/с = 10 кг•м/с и направлен в сторону скорости v.

 Пример 5.
Заряд q = −7,5 нКл помещен в электрическое поле с напряженностью E =  400 В/м. Найти модуль и направление силы, действующей на заряд.

Сила равна  F = qE. Так как заряд отрицательный, то вектор силы направлен в сторону, противоположную вектору E. (рис. 11)

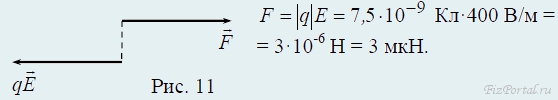
 Деление вектора a на скаляр k равнозначно умножению a на 1/k.
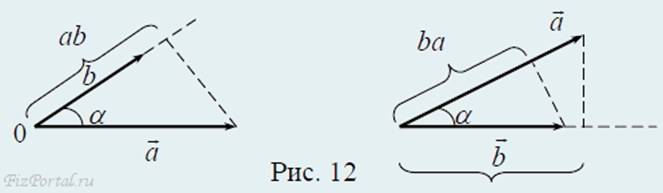
 Скалярным произведением векторов a и b называют скаляр «c», равный произведению модулей этих векторов на косинус угла между ними

(a•b) = (b•a) = c,

с = ab•cosα (рис. 12)

 Пример 6.
Найти работу постоянной силы F = 20 Н, если перемещение S = 7,5 м, а угол α между силой и перемещением α = 120°. 

Работа силы равна по определению скалярному произведению силы и перемещения 

A = (F•S) = FScosα = 20 H × 7,5 м × cos120° = −150 × 1/2 = −75 Дж.

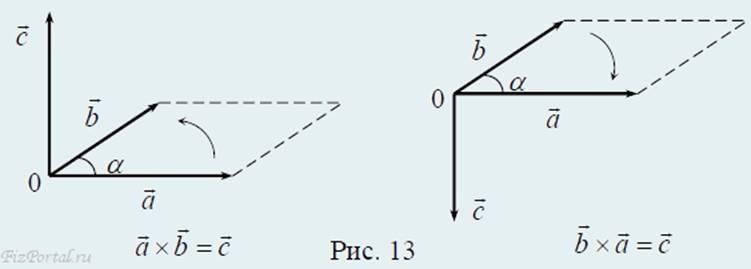
 Векторным произведением векторов a и b называют вектор c, численно равный произведению модулей векторов a и b, умноженных на синус угла между ними:

с = a × b = [a, b],

с = ab × sinα.

Вектор  c перпендикулярен плоскости, в которой лежат векторы a и b, причем его направление связано с направлением векторов a и b правилом правого винта (рис. 13).

 Пример 7.
Определить силу, действующую на проводник длиной 0,2 м, помещенный в  магнитном поле, индукция которого 5 Тл, если сила тока в проводнике 10 А и он образует угол α = 30° с направлением поля.

Сила Ампера 

dF = I[dl, B] = Idl × B или F = I(l)∫{dl × B},

F = IlBsinα = 5 Тл × 10 А × 0,2 м × 1/2 = 5 Н.

 Рассмотрите решение задач.
1. Как направлены два вектора, модули которых одинаковы и равны a, если  модуль их суммы равен: а) 0; б) 2а; в) а; г) a√{2}; д) a√{3}?

 Решение.
а) Два вектора направлены вдоль одной прямой в противоположные стороны. Сумма этих векторов равна нулю. 

б) Два вектора направлены вдоль одной прямой в одном направлении. Сумма этих векторов равна 2a. 

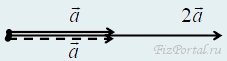
в) Два вектора направлены под углом 120° друг к другу. Сумма векторов  равна a. Результирующий вектор находим по теореме косинусов:

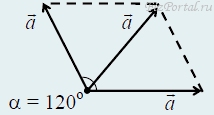
a² + a² + 2aacosα = a²,

cosα = −1/2 и α = 120°.

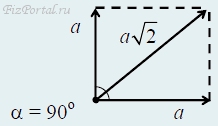
г) Два вектора направлены под углом 90° друг к другу. Модуль суммы равен 

a² + a² + 2aacosα = 2a²,

cosα = 0 и α = 90°.

д) Два вектора направлены под углом 60° друг к другу. Модуль суммы равен 

a² + a² + 2aacosα = 3a²,

cosα = 1/2 и α = 60°.

 Ответ: Угол α между векторами равен: а) 180°; б) 0; в) 120°; г) 90°; д) 60°.

2. Если  a = a₁ + a₂ ориентации векторов, то, что можно сказать о взаимной ориентации векторов a₁ и a₂, если: а) a = a₁ + a₂; б) a² = a₁² + a₂²; в) a₁ + a₂ = a₁ − a₂?

 Решение.
а) Если сумма векторов находится как сумма модулей этих векторов, то  вектора направлены вдоль одной прямой, параллельно друг другу a₁||a₂.
б) Если вектора направлены под углом друг к другу, то их сумма находится по теореме косинусов для параллелограмма 

a₁² + a₂² + 2a₁a₂cosα = a²,

cosα = 0 и α = 90°.

вектора перпендикулярны друг другу a₁ ⊥ a₂.
в) Условие  a₁ + a₂ = a₁ − a₂ может выполниться, в случае если a₂ − нулевой вектор, тогда a₁ + a₂ = a₁.
 Ответы. а) a₁||a₂; б) a₁ ⊥ a₂; в) a₂ − нулевой вектор.

3. Две силы по 1,42 H каждая приложены к одной точке тела под углом  60° друг к другу. Под каким углом надо приложить к той же точке тела две силы по 1,75 H каждая, чтобы действие их уравновешивало действие первых двух сил?

Решение. 
По условию задачи две силы по 1,75 Н уравновешивают две силы по 1,42 Н.  Это возможно, если равны модули результирующих векторов пар сил. Результирующий вектор определим по теореме косинусов для параллелограмма. Для первой пары сил:

F₁² + F₁² + 2F₁F₁cosα = F²,

для второй пары сил, соответственно

F₂² + F₂² + 2F₂F₂cosβ = F².

Приравняв левые части уравнений

F₁² + F₁² + 2F₁F₁cosα = F₂² + F₂² + 2F₂F₂cosβ.

Найдем искомый угол β между векторами

cosβ = (F₁² + F₁² + 2F₁F₁cosα − F₂² − F₂²)/(2F₂F₂).

После вычислений,

cosβ = (2•1,422 + 2•1,422•cos60° − 2•1,752)/(2•1,752) = −0,0124,

β ≈ 90,7°.

 Второй способ решения.
Рассмотрим проекцию векторов на ось координат ОХ (рис.). 

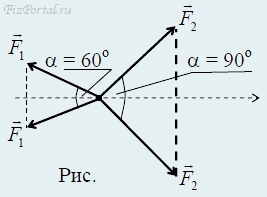
Воспользовавшись соотношением между сторонами в прямоугольном треугольнике, получим 

2F₁cos(α/2) = 2F₂cos(β/2),

откуда

cos(β/2) = (F₁/F₂)cos(α/2) = (1,42/1,75) × cos(60/2) и β ≈ 90,7°.

4. Вектор  a = 3i − 4j. Какова должна быть скалярная величина c, чтобы |ca| = 7,5?
 Решение.

ca = c(3i − 4j) = 7,5

Модуль вектора a будет равен

a² = 3² + 4², и a = ±5,

тогда из

c•(±5) = 7,5,

найдем, что

c = ±1,5.

5. Векторы  a₁ и a₂ выходят из начала координат и имеют декартовы координаты концов {6, 0} и {1, 4}, соответственно. Найдите вектор a₃ такой, что: а) a₁ + a₂ + a₃ = 0; б) a₁ − a₂ + a₃ = 0.

 Решение.
Изобразим векторы в декартовой системе координат (рис.) 

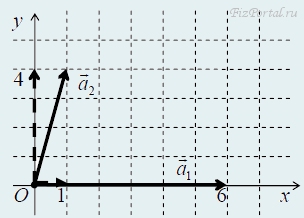
а) Результирующий вектор вдоль оси Ox равен 

a_x = 6 + 1 = 7.

Результирующий вектор вдоль оси Oy равен

a_y = 4 + 0 = 4.

Чтобы сумма векторов была равна нулю, необходимо, чтобы выполнялось условие

a₁ + a₂ = −a₃.

Вектор a₃ по модулю будет равен суммарному вектору a₁ + a₂, но направлен в противоположную ему сторону. Координата конца вектора a₃ равна {−7, −4}, а модуль

a₃ = √{7² + 4²} = 8,1.

б) Результирующий вектор вдоль оси Ox равен 

a_x = 6 − 1 = 5,

а результирующий вектор вдоль оси Oy

a_y = 4 − 0 = 4.

При выполнении условия

a₁ − a₂ = −a₃,

вектор a₃ будет иметь координаты конца вектора a_x = –5 и a_y = −4, а модуль его равен

a₃ = √{5² + 4²} = 6,4.

6. Посыльный проходит 30 м на север, 25 м на восток, 12 м на юг, а  затем в здании поднимается на лифте на высоту 36 м. Чему равны пройденный им путь L и перемещение S?

 Решение.
Изобразим ситуацию, описанную в задаче на плоскости в произвольном масштабе (рис.). 

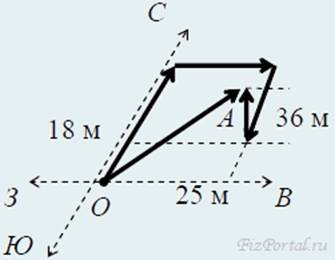
Конец вектора OA имеет координаты 25 м на восток, 18 м на север и 36 вверх (25; 18; 36). Путь, пройденный человеком равен

L = 30 м + 25 м + 12 м +36 м = 103 м.

Модуль вектора перемещения найдем по формуле

S = √{(x − x_o)² + (y − y_o)² + (z − z_o)²},

где x_o = 0, y_o = 0, z_o = 0.

S = √{25² + 18² + 36²} = 47,4 (м).

 Ответ: L = 103 м, S = 47,4 м.

7. Угол α между двумя векторами  a и b равен 60°. Определите длину вектора с = a + b и угол β между векторами a и c. Величины векторов равны a = 3,0 и b = 2,0.

 Решение.
Длину вектора, равного сумме векторов  a и b определим воспользовавшись теоремой косинусов для параллелограмма (рис.).

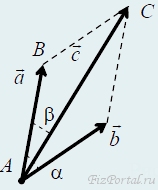
с = √{a² + b² + 2abcosα}.

После подстановки

с = √{3² + 2² + 2•3•2•cos60°} = 4,4.

Для определения угла β воспользуемся теоремой синусов для треугольника ABC:

b/sinβ = a/sin(α − β).

При этом следует знать, что

sin(α − β) = sinαcosβ − cosαsinβ.

Решая простое тригонометрическое уравнение, приходим к выражению 

tgβ = bsinα/(a + bcosα),

следовательно,

β = arctg(bsinα/(a + bcosα)),

β = arctg(2•sin60/(3 + 2•cos60)) ≈ 23°.

Сделаем проверку, воспользовавшись теоремой косинусов для треугольника: 

a² + c² − 2ac•cosβ = b²,

откуда

cosβ = (a² + c² − b²)/(2ac)

и

β = arccos((a² + c² − b²)/(2ac)) = arccos((3² + 4,4² − 2²)/(2•3•4,4)) = 23°.

 Ответ: c ≈ 4,4; β ≈ 23°.

 Решите задачи.
8. Для векторов  a и b, определенных в примере 7, найдите длину вектора d = a − b угол γ между a и d.

9. Найдите проекцию вектора  a = 4,0i + 7,0j на прямую, направление которой составляет угол α = 30° с осью Ox. Вектор a и прямая лежат в плоскости xOy.

10. Вектор  a составляет угол α = 30° с прямой АВ, a = 3,0. Под каким углом β к прямой АВ нужно направить вектор b (b = √{3}), чтобы вектор с = a + b был параллелен АВ? Найдите длину вектора c.

11. Заданы три вектора:  a = 3i + 2j − k; b = 2i − j + k; с = i + 3j. Найдите а) a + b; б) a + c; в) (a, b); г) (a, c)b − (a, b)c.

12. Угол между векторами  a и b равен α = 60°, a = 2,0, b = 1,0. Найдите длины векторов с = (a, b)a + b и d = 2b − a/2.

13. Докажите, что векторы  a и b перпендикулярны, если a = {2, 1, −5} и b = {5, −5, 1}.

14. Найдите угол α между векторами  a и b, если a = {1, 2, 3}, b = {3, 2, 1}.

15. Вектор  a составляет с осью Ox угол α = 30°, проекция этого вектора на ось Oy равна a_y = 2,0. Вектор b перпендикулярен вектору a и b = 3,0 (см. рис.).

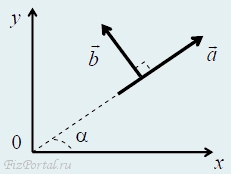
Вектор с = a + b. Найдите: a) проекции вектора b на оси Ox и Oy; б) величину c и угол β между вектором c и осью Ox; в) (a, b); г) (a, c).

 Ответы:
9. a ₁ = a_xcosα + a_ysinα ≈ 7,0.
10. β = 300°; c = 3,5. 
11. а) 5i + j; б) i + 3j − 2k; в) 15i − 18j + 9 k. 
12. c = 2,6; d = 1,7. 
14. α = 44,4°. 
15. а) b _x = −1,5; b_y = 2,6; б) с = 5; β ≈ 67°; в) 0; г) 16,0.

Операции над векторами

Над векторами по определённым правилам можно выполнять линейные операции: складывать их, умножать на число, вычитать. Введём линейные операции над векторами.

Произведением вектора

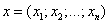
на действительное число 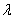называется вектор

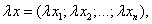
т.е. при умножении вектора на число каждая его координата умножается на это число.

Зная вектор

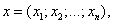
можно получить противоположный вектор

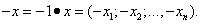
Суммой векторов

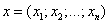
и

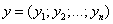
называется вектор

,

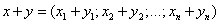т.е. при сложении векторов одной и той же размерности их соответствующие координаты почленно складываются.

Если в плане продаж сети торговых предприятий продажи товаров определить как положительные уровни товаров, а затраты на продажи – как отрицательные, то получим вектор затрат-продаж

,

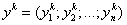где

-

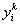продажи (затраты) k – м предприятием товара i, а k = 1, 2, 3,…, m .

Суммарный вектор затрат-продаж y определяется суммированием векторов затрат-продаж всех mпредприятий сети:

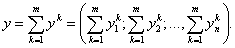
Сумма противоположных векторов даёт нулевой вектор:

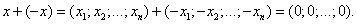
При вычитании двух векторов одной и той же размерности их соответствующие координаты почленно вычитаются:

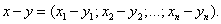
Линейные операции над векторами удовлетворяют следующим свойствам.

Свойство 1.

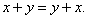
Свойство 2.

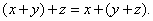
Свойство 3.

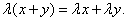
Свойство 4.

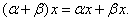
Свойство 5.

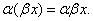
Свойство 6.

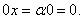
Скалярным произведением двух векторов

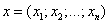
и

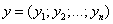
называется число

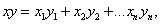
равное сумме произведений соответствующих координат векторов.

В экономических задачах можно рассматривать скалярное произведение вектора цен p
на вектор объёма проданных товаров x . Скалярное произведение px в этом случае даёт суммарную стоимость проданных товаров x при ценах p . Например, если объём всех товаров, проданных предприятием, выражается вектором x = (400; 750; 200; 300), элементы которого означают соответственно количество товаров различных групп, а цены в одних и тех же денежных единицах заданы в соответствующем порядке вектором p = (3; 2,1; 1,2; 0,5), то скалярное произведение

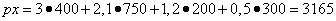
выражает суммарную стоимость всех товаров x .

Скалярное произведение векторов обладает следующими свойствами:

Свойство 1.

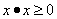, причём 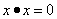лишь при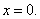

Свойство 2.

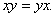
Свойство 3.

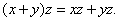
Свойство 4.

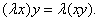
Число

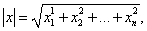
равное квадратному корню из суммы квадратов координат вектора, называется модулем (или длиной) вектора

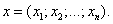
Пример 1.Найти длину вектора x = (3; 0; 4).

Решение. Длина вектора равна

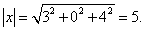
Два вектора называют ортогональными, если их скалярное произведение равно нулю.

Пример 2.Ортогональны ли векторы x = (3; 0; 1; -1) y = (-2; 5; 6; 0)?

Решение. Найдём скалярное произведение

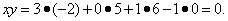
Итак, два данных вектора ортогональны.

Б) Скалярное произведение

Скалярное произведение векторов 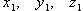и :

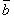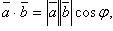
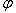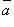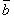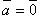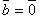где - угол между векторами и ; если либо , то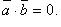

Из определения скалярного произведения следует, что 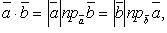где, например, 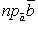есть величина проекции вектора 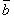на направление вектора .

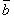Скалярный квадрат вектора: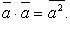

Свойства скалярного произведения: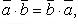

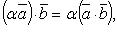
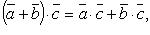
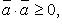
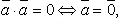
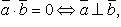
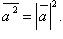
Скалярное произведение в координатах

Если 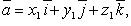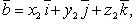то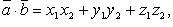

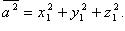
Угол между векторами

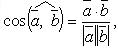
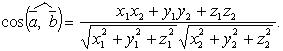
Векторное произведение

Векторное произведение векторов 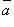и 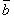- вектор, обозначаемы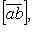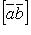й или 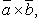для когорого:

1) 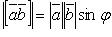( 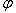- угол между векторам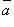и и , );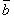

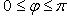2)

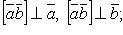
3) тройка 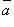, , 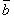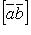- правая.

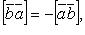
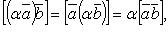
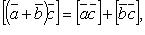
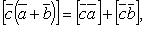
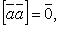
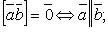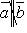Свойства векторного произведения: если , то 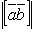равен площади параллелограмма, построенного на приведенных к общему началу векторах 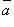и .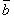

Алгебра (логика) высказываний