Условие параллельности и перпендик-сти прямой и плоскости
Угол φ между прямой, заданной каноническими уравнениями
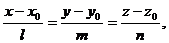 и плоскостью, определяемой общим уравнением
и плоскостью, определяемой общим уравнением
Ax + By + Cz + D = 0, можно рассматривать как дополнительный к углу ψ между направляющим вектором прямой и нормалью к плоскости. Тогда
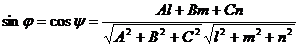
Условием параллельности прямой и плоскости является при этом условие перпендикулярности векторов n и а:
Al + Bm + Cn = 0,
а условием перпендикулярности прямой и плоскости – условие параллельности этих векторов: A/l = B/m = C/n.
Вопрос
Понятие функции. Свойства задания и основные свойства
Функцией называется закон, по которому числу х из заданного множества Х, поставлено в соответствие только одно число у, пишут 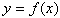 , при этом x называют аргументом функции, y называют значением функции.
, при этом x называют аргументом функции, y называют значением функции.
Существуют разные способы задания функций.
1. Аналитический способ.
Аналитический способ - это наиболее часто встречающийся способ задания функции.
Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например 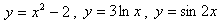 .
.
Рассмотрим первый пример - 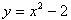 . Здесь значению x = 1 соответствует
. Здесь значению x = 1 соответствует 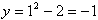 , значению x = 3 соответствует
, значению x = 3 соответствует 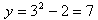 и т. д.
и т. д.
Функция может быть задана на разных частях множества X разными функциями.
Например:
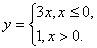
Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а справа формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно.
Например 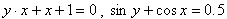 . Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:
. Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:
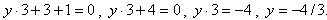 . То есть, значение функции при х = 3 равно -4/3.
. То есть, значение функции при х = 3 равно -4/3.
При аналитическом способе задания, функция может быть задана параметрически - это, когда х и у выражены через некоторый параметр t. Например,
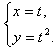
Здесь при t = 2, x = 2, y = 4. То есть, значение функции при х = 2 равно 4.
2. Графический способ.
При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом 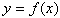 . Пример:
. Пример:
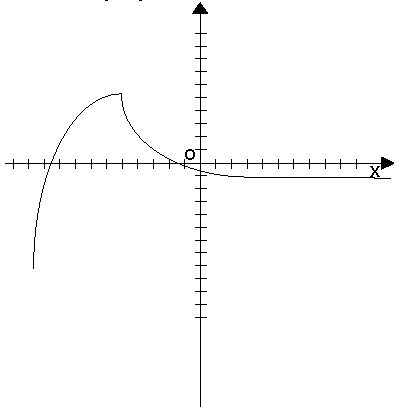
3. Словесный способ.
Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.
«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».
4. Табличный способ.
Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.
Пример:

Табличный способ задания функции очень удобен при обработке результатов исследований.
Основные свойства функции.
1) Четность и нечетность. Функция 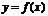 называется четной, если для любых значений
называется четной, если для любых значений 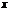 из области определения
из области определения 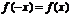 и нечетной, если
и нечетной, если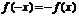 . В противном случае функция
. В противном случае функция 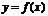 называется функцией общего вида.
называется функцией общего вида.
Пример.
а) Функция 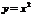 - четная (рис.3.3 а). т.к - четная (рис.3.3 а). т.к 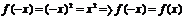 ; б) Функция ; б) Функция 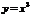 - нечетная (рис.3.3 б). - нечетная (рис.3.3 б). 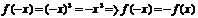 ; в) Функция ; в) Функция 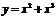 - общего вида (рис.3.3 в). - общего вида (рис.3.3 в). 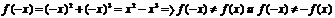 . . |  |
График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
2) Монотонность. Функция 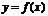 называется возрастающей (убывающей) на промежутке
называется возрастающей (убывающей) на промежутке 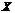 , если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. Функции возрастающие и убывающие называются монотонными функциями.
, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. Функции возрастающие и убывающие называются монотонными функциями.
Пример.
1) Функция - на интервале - на интервале 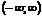 монотонно возрастает (рис.3.4а). 2) Функция монотонно возрастает (рис.3.4а). 2) Функция 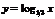 - на интервале - на интервале 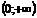 монотонно убывает (рис.3.4 б). монотонно убывает (рис.3.4 б). | 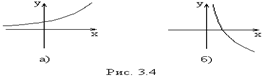 |
3) Ограниченность. Функция 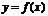 называется ограниченной на промежутке
называется ограниченной на промежутке 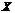 , если существует такое положительное число
, если существует такое положительное число 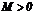 , что
, что 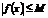 для любого
для любого 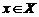 . В противном случает функция называется неограниченной.
. В противном случает функция называется неограниченной.
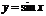 - ограничена на всей числовой оси, т.к.
- ограничена на всей числовой оси, т.к. 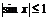 для любого
для любого 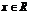 .
.
4) Периодичность. Функция 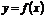 называется периодической с периодом
называется периодической с периодом 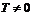 , если для любых
, если для любых 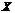 из области определения функции
из области определения функции 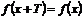 .
.
Пример.
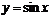 , период , период 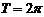 , т.к. для любых , т.к. для любых 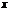 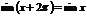 . . |  |
Вопрос
