Свойство цилиндрических поверхностей.

Если некоторая точка M₀(x₀, y₀, z₀) принадлежит цилиндрической поверхности, описываемой уравнением F(x, y) = 0 , то все точкипрямой, проходящей через эту точку параллельно оси OZ , также принадлежат цилиндрической поверхности. Такие прямые называются образующими цилиндрической поверхности, а кривая, описываемая уравнением F(x, y) = 0 и получающаяся в сечении любой плоскостью z = h , называется направляющей.

Примеры цилиндрических поверхностей 2–го порядка.

Эллиптический цилиндр.Уравнение

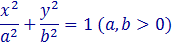
в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является эллипсс полуосями a и b (рис. 1).

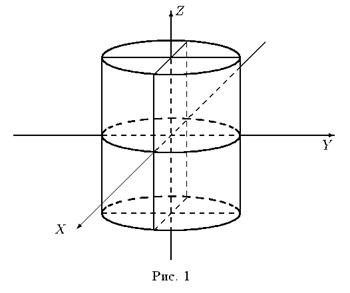
В частности, уравнение x² + y² = R² в трехмерном пространстве определяет круглый цилиндр.

Гиперболический цилиндр. Уравнение

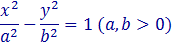
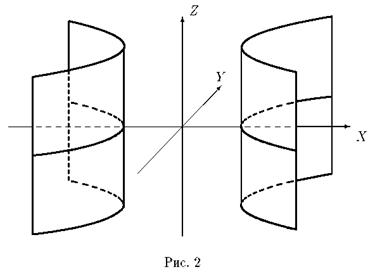
в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является гиперболас полуосями a и b (рис. 2).

Параболический цилиндр. Уравнение

y2 = 2px ( p>0 )

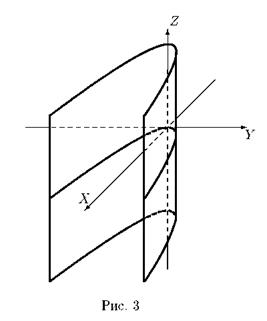
в трехмерном пространстве определяет цилиндрическую поверхность с образующими, параллельными оси OZ , направляющей является парабола (рис. 3).

Вопрос 20. Линейные пространства.Основныепонятия.Теорема о Базисе.

Множество L называется линейным или векторным пространством, если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо:

1. Каждой паре элементов x и y из L отвечает элемент x + yиз L, называемый суммой x и y, причём:

x + y = y + x− сложение коммутативно;

x + (y + z) = (x + y) + z− сложение ассоциативно;

x +0= x − существует единственный нулевой элемент 0( x +0= x для любого x из L);

x + (− x)= 0 − для каждого элемента x из L существует единственный противоположный элемент −x ( x + (−x) = 0для любого x из L).

2. Каждой паре x и α, где α −число, а x элемент из L, отвечает элемент α·x, наываемый произведением α и x, причём:

α·(β·x) = (α·β)·x − умножнение на число ассоциативно: ;

1·x = x − для любого элемента x из L.

3. Операции сложения и умножения на число связаны соотношениями:

α·(x + y) = α·x + α·y − умножнение на число дистрибутивно относительно сложения элементов;

(α + β)·x = α·x + β·x − умножнение на вектор дистрибутивно относительно сложения чисел.

Определение:Если в пространстве Lимеются векторы линейного преобразования 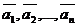, то другой вектор 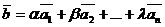является линейной комбинацией векторов .

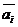Определение:Если 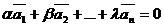только при a = b = … = l = 0, то векторы 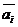называются линейно независимыми.

Определение:Если в линейном пространстве Lесть n линейно независимых векторов, но любые n + 1 векторов линейно зависимы, то пространство Lназывается n-мерным, а совокупность линейно независимых векторов называется базисом линейного пространства L.

Утверждение: все максимально линейно независимые системы векторов имеют одинаковое количество векторов.

Доказательство (теорема о базисе):

Пусть есть 2-е линейно независимые системы векторов, с разным количеством векторов, тогда любой вектор линейного пространства выражается линейно через вектора этих систем.

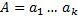
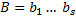
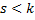
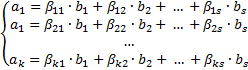, где

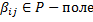
Система s-ок: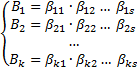

имеет векторов больше чем Sи поэтому линейно зависима, следовательно существует набор скаляров 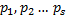для которого 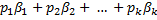равна нулю.

Домножим строчки 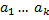на этот набор скаляров:

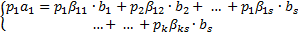слева положим линейную комбинацию системы векторов А, где не все коэффициенты равны нулю. А справа раскрыв скобки получим следующий коэффициент при :

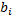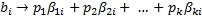
Это i-ая координата выбранной линейной комбинации векторов системы B и она равна нулю. Значит система векторовт А линейно зависима. Поэтому возникает противоречие.

Вопрос 21. Матрица перехода от Базиса к Базису.

L -n- мерное линейное пространство с базисом 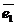, ,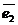…, 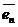. Другой базис задан векторами 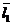, 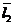.. . 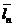Тогда они также являются векторами этого пространства и их можно представить в виде линейной комбинации векторов , ,…, :

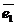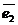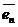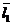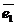= a₁₁ + a₂₁ 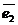+…+ a_n1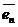

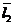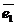= a₁₂ + a₂₂ 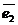+…+ a_n2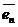

……………………………….

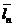= a_n1 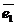+ a_n2 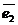+…+ a_nn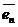

Тогда матрица 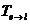= 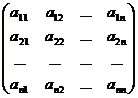называется матрицей перехода от базиса к базису.

Вопрос 22. Линейный оператор и его матрица.

Линейным оператором в линейном пространстве Lназывается всякое отображение A :L=>Lпространства Lв себя , обладающее свойствами:

A(tx)=tAx , A(x+y)=Ax+Ay

Пусть A– линейный оператор в конечномерном пространстве L_nи B = (l₁,….,l_n) –некоторый фиксированный базис. Разложим векторы Ae_k, k=1, … , n, по базису B :

Ae_k= a_1ke₁+…..+a_nke_n, k=1,….,n.

Тогда матрица

A=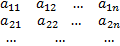

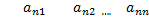
Называется матрицей оператора Aв базисе B. Матрицу оператора будем иногда обозначать также символом [A].

Пусть Aи A’ – матрицы оператора Aв базисах Bи B’ , а T = T_B->B’ – матриа перехода от базиса Bк базису B’. Тогда формула преобразования матрицы оператора пи преобразовании базиса имеет вид

A’=T^-1AT.

Практическая часть:

Правило для решения : Работа с операторами не проводится, проводится только с их матрицами.

Вопрос 23. Собственные значения и собственные векторы линейных операторов.

Определение: Пусть L – заданное n- мерное линейное пространство. Ненулевой вектор 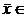L называется собственным вектором линейного преобразования А, если существует такое число l, что выполняется равенство:

A .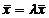

При этом число l называется собственным значением (характеристическим числом) линейного преобразования А, соответствующего вектору .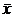

Определение: Если линейное преобразование А в некотором базисе 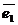, ,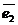…, 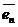имеет матрицу А = 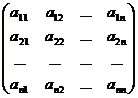, то собственные значения линейного преобразования А можно найти как корни l₁, l₂, … ,l_n уравнения:

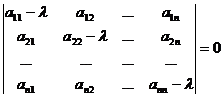
Это уравнение называется характеристическим уравнением, а его левая часть-характеристическим многочленом линейного преобразования А.

Следует отметить, что характеристический многочлен линейного преобразования не зависит от выбора базиса.

!!!ДОКАЗАТЬ Ax=Lx!!!

Вопрос 24.Приведение уравнения 2-го порядка к каноническому виду(Алгоритм, с примером).

!!!!СДЕЛАТЬ!!!

Вопрос 25.Множество операций над множеством.

Множество – аксиоматическое понятие, неопределяемое.

Множество Mсостоящее из нескольких количественных элементов принято записывать:M ={ x₁,x₂…,x_n}

Пустое множество ( ) – множество в котором ничего нет.

Множество u (универсом) – это множество всех элементов.

Операции над множествами.

1)Объединения. Двух Множеств M₁и M₂наз-ся множество M , которое содержит все элементы множестM₁и M₂и только.Обозначается U .Пример:M₁ UM₂ = M .

На диограммеВейлера – Етта объединение будет выглядеть так:

2)Пересечение двух множестM₁и M_{2 ,} называется множество Mв котором содержится все элементы принадлежащие одновременно и M₁и M_2.

Обозначается как объединение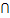

Выглядит вот так:M₁U(НИЗ ГОЛОВОЙ) M₂= M

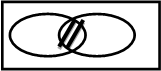3) Дополнением, множества M (Mс чертой сверху) – называется множество состоящее из всех элементов не лежащих в M. Иногда называют так же отрицанием.

Дополнение.

Свойство.

1) M(С ЧЕРТОЙ) UM = u (универсум)

2) M(С ЧЕРТОЙ) U (НИЗ ГОЛОВОЙ) =

В

А

Подмножеством Bмножества A( Bвключает A) – называется множество состоящее только из элементов A .

Несобственным подмножеством множества А называется пустое множество и само множество А. Все остальные подмножества называются собственными.
Прямое произведение А и В (АхВ) - множество С состоящее из всевозможных упорядоченных пар, на первом месте в которых располагаются элементы множества А, а на втором элементы множества В

Пример:

A = {1,2,3} , B= {1,5,6}, АхВ = { (1,1) , (1,5) , (1,6) ; (2,1) , (2,5) , (2,6) ; (3,1) , (3,5) (3,6) }

Если множества конечны и их мощности равны Nи M , то их прямое произведение имеет NхM.

Пишут что элемент Xлежит в множестве Aи обозначает это xпринадлежит A, если содержится среди элементов A .

Пример:A {1,2,3} , тогда 5 не принадлежит A , а 1 принадлежит A.

Квантер принадлежности ? можно ставить только после множества элемента A.

Разность двух множеств Aи B( A \ B) это множества элементов лежащих в A , но не лежащих в B .

Симметрическую разностью A 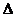Bназывается объединение разность А без В , В без А

Равенство множеств.

Два множества равны, если все их элементы равны между собой. И множества равномощны если они содержат одинаковое кол-во элементов, или можно установить взаимное однозначное соотвествие между элементами этих множеств.

Пример:M₁= { 1,2,3,4} , M₂ = { Вася, Петя , Ваня , Аня }

Вопрос 26.Докозательсво , что множество действительных числе не .

Начнем двигаться из левого верхнего угла таблицы и нумеровать дроби по порядку, исключая те, которые встречались ранее.

Докажем, что множество натуральных чисел равномощны множеству рациональных. Запишем таблицу.
Разместим в таблицу рациональные числа с числителем с номером строки и знаменателем с номером столбца.

					В этой таблице нашим способом можно дойти до любого рационального числа. При этом каждому рациональному числу соответствует его натуральный номер. Таким образом между положительными рациональными числами и натуральными числами установлено взаимно однозначное соответствие. Они равномощны.
…	…	…	…	…	…

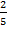С рациональными отрицательными числами установлено взаимно-однозначное соответствие таким же образом, как между натуральными и целыми.