Уравнение прямой в пространстве, проходящей

через две точки.

Если на прямой в пространстве отметить две произвольные точки M₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:

.

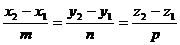Кроме того, для точки М₁ можно записать:

.

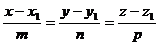Решая совместно эти уравнения, получим:

.

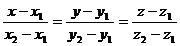Это уравнение прямой, проходящей через две точки в пространстве.

Общие уравнения прямой в пространстве.

Общие уравнения прямой в координатной форме:

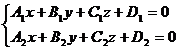
Практическая задача часто состоит в приведении уравнений прямых в общем виде к каноническому виду.

Для этого надо найти произвольную точку прямой и числа m, n, p.

При этом направляющий вектор прямой может быть найден как векторное произведение векторов нормали к заданным плоскостям.

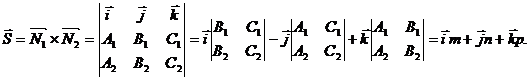
Вопрос 18. Метод сечений в пространстве.Эллипсоиды и гиперболоиды.(С примерами).

Определение.Поверхности второго порядка – это поверхности, уравнения которых в прямоугольной системе координат являются уравнениями второго порядка.

Цилиндрические поверхности.

Эллипсоидом называется поверхность, которая в некоторой декартовой системе координат определяется уравнением

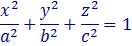
где a, b, c>0 — параметры эллипсоида. Это уравнение называется каноническим уравнением эллипсоида, а система координат, в которой эллипсоид описывается каноническим уравнением, называется канонической.

Из уравнения эллипсоида следует, что поверхность симметрична относительно координатных плоскостей, начало координат является центром эллипсоида.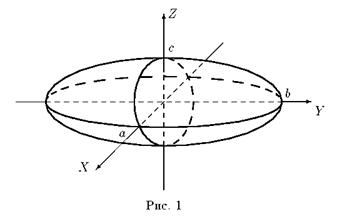

Исследуем форму эллипсоида с помощью метода сечений (рис.1).

Рассмотрим сечения эллипсоида плоскостями z = h , параллельными плоскости XOY (z=h):

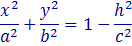
При | h |<c в сечении получается эллипсы с полуосями.

При h = ± c плоскость z = h касается эллипсоида в точках (0, 0, ± c) .

При | h |>c плоскость z = h не пересекает эллипсоид (в сечении — пустое множество).

Аналогично исследуется сечения по другим плоскостям XOZ(y=0),YOZ (x=0). Получится

y=0 : 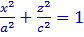и при x=0 :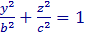

Любое сечение эллипса параллельное координатным плоскостям будет эллипс.

Гиперболоид.

Однополостным гиперболоидом называется поверхность, которая в некоторой декартовой системе координат определяется уравнением

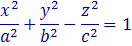
где a, b, c>0 — параметры гиперболоида. Это уравнение называется каноническим уравнением однополостного гиперболоида, а система координат, в которой гиперболоид описывается каноническим уравнением, называется канонической.

Исследуем форму однополостного гиперболоида с помощьюметода сечений (рис.1)

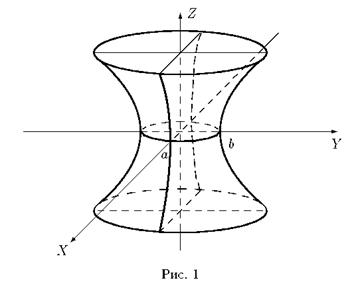
Рассмотрим сечения гиперболоида плоскостями z = h , параллельными плоскости XOY (z=h):

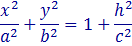
При любых значениях h в сечении получается эллипсы с полуосями.

Аналогично исследуются сечения гиперболоида плоскостями, параллельными координатным плоскостями XOZ (y=0) и YOZ (x=0). В частности,

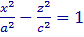– т. е. в сечении координатной плоскостью y = 0 получается гипербола, вершины которой лежат на оси OX , и 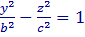т. е. в сечении координатной плоскостью x = 0 также получается гипербола, вершины которой лежат на оси OY

Двуполостный гиперболоид.

Двуполостным гиперболоидом называется поверхность, которая в некоторой декартовой системе координат определяется уравнением

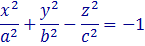
где a, b, c>0 — параметры гиперболоида. Это уравнение называется каноническим уравнением двуполотного гиперболоида, а система координат, в которой гиперболоид описывается каноническим уравнением, называется канонической.

Исследуем форму двуполостного гиперболоида с помощью метода сечений (рис.2).

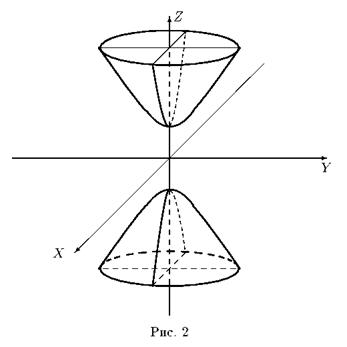
Рассмотрим сечения гиперболоида плоскостями z = h , параллельными плоскости XOY :

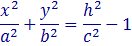
При | h |>c в сечении получается эллипсы с полуосями. При h =± c плоскость z = h касаетсягиперболоида в точках (0, 0, ± c) и, наконец, при | h |<c плоскость z = h не пересекает гиперболоида (в сечении — пустое множество)

Аналогично исследуются сечения гиперболоида плоскостями, параллельными координатным плоскостями XOZ и YOZ . В частности

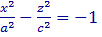т. е. в сечении координатной плоскостью y = 0 получается гипербола, вершины которой лежат на оси OZ , и 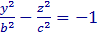т. е. в сечении координатной плоскостью x = 0 также получается гипербола, вершины которой лежат на оси OZ .

Вопрос 19. Метод сечений.Цилиндры и Конусы.(С примерами).

Конусом 2 –ого порядка называется поверхность, которая в некоторой декартовой системе координат определяется уравнением
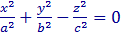где a, b, c>0 — параметры конуса.Это уравнение называется каноническим уравнением конуса, а система координат, в которой конус описывается каноническим уравнением, называется канонической.

Исследуем форму конуса с помощью метода сечений (рис. 1).

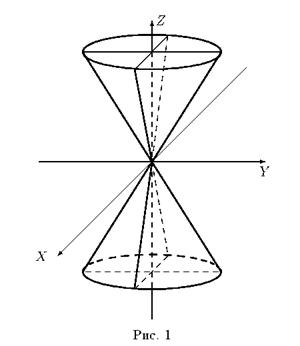
Рассмотрим сечения плоскостями z = h , параллельными плоскости XOY :

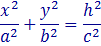
При любых значениях h ≠ 0 в сечении получается эллипсы с полуосямиПри h = 0 в сечении получается точка — начало координат.

Аналогично исследуются сечения конуса плоскостями, параллельными координатным плоскостями XOZ и YOZ . В частности,

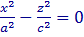т.е. в сечении координатной плоскостью y = 0 получается пара прямых, пересекающихся в начале координат. Аналогично 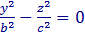т.е. в сечении координатной плоскостью x = 0 также получается пара прямых, пересекающихся в начале координат.

Цилиндр

Цилиндрической поверхностью называется поверхность, которая в некоторой декартовой системе координат определяется уравнением, в котором не фигурирует одна из переменных:

F(x, y) = 0, F(x, z) = 0 или F(y, z) = 0.