Свойства скалярного произведения (cдокозательсвом)

1. Скалярное произведение обладает переместительным свойством: ab=ba

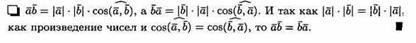
Решение:

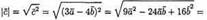
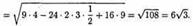
Если рассматривать векторы 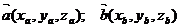в декартовой прямоугольной системе координат, то

× = x_ax_b+ y_ay_b + z_az_b;

Используя полученные равенства, получаем формулу для вычисления угла между векторами:

;

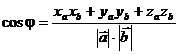Вопрос 10. Векторное произведение векторов. Свойства.

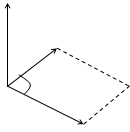
Определение.Векторным произведениемвекторов и называется вектор , удовлетворяющий следующим условиям:

1) 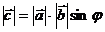, где j - угол между векторами и ,

2) вектор 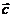ортогонален векторам и

3) , и 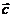образуют правую тройку векторов.

Обозначается: 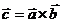или .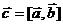

j

Векторное пространство, в котором задано скалярное произведение , называется евклидовым.

Свойства векторного произведения векторов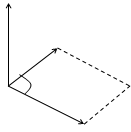

1) 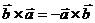; - Длина вектора остается неизменной , но порядок bи aменяется.

2) 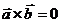, если ïï или = 0 или = 0;

3) (m )´ = ´(m ) = m( ´ );m>0. В случает когда m<0 при вынесении mиз векторного произведения со знаком минус, меняется так же направление a.

4) ´( + 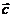) = ´ + ´ 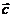;!!!!ДОКАЗАТЬ СВОЙСТВО!!!!

5) Если заданы векторы (x_a, y_a, z_a)и (x_b, y_b, z_b) в декартовой прямоугольной системе координат с единичными векторами 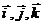, то

´ =

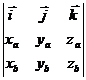
Вопрос 11. Смешанное произведение. Свойства

Сме́шанноепроизведе́ние 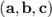векторов 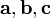— скалярное произведение вектора 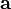на векторное произведение векторов 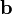и :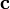

.

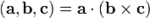
Смешанное произведение 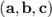по модулю равно объему параллелепипеда, построенного на векторах , и .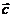

Свойствасмешанного произведения:

1)Смешанное произведение равно нулю, если:

а)хоть один из векторов равен нулю;

б)два из векторов коллинеарны;

в)векторы компланарны.

2)

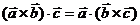
3)

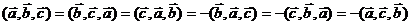
4)

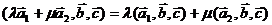
5) Объем треугольной пирамиды, образованной векторами , и 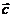, равен

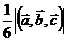
6)Если 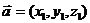, , 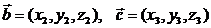то

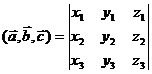
Используя координатную запись скалярного и векторного произведения, запишем:

[ab]c = (Y_aZ_b – Y_bZ_a)X_c + (X_bZ_a – X_aZ_b)Y_c + (X_aY_b – X_bY_a)Z_c = .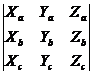

Вопрос 12. Преобразование координат на плоскости. Парралельный перенос. Поворот.

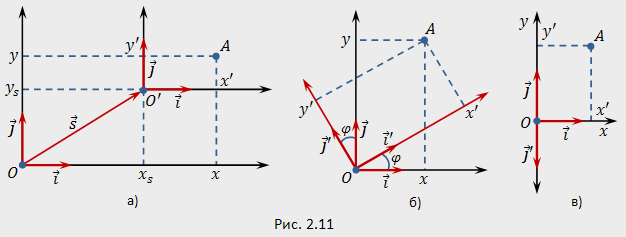
Преобразование прямоугольной системы координат

оси «новой системы координат» 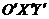параллельны соответствующим осям « старой системы координат» 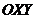и имеют одинаковые направления с ними (параллельный перенос системы координат).

Пусть начало новой системы координат 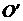имеет координаты 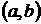в старой системе координат. Точка 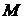плоскости со «старыми координа­тами» 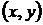будет иметь неко­торые «новые координаты» 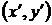. Из рис.1 получаем

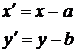Рис.1

, (1)

то есть новые координаты точки равны ее старым координатам минус старые координаты нового начала.

Обратно из (1) находим

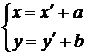(2)

Пусть теперь «новая система» координат , при неизменном начале , повернута относительно старой системы на угол 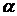, т.е. 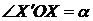, причем угол 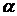считается положительным, если поворот осуществляется против часовой стрелки и отрицательным – в противоположном случае (рис.2).

Обозначим через 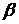угол, образованный радиусом-вектором 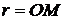точки 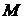с осью 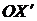; тогда отрезок 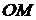, с учетом знака 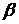, будет составлять с осью 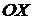угол 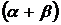. Отсюда на основании формул при любом расположении точки 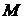имеем:

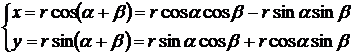(3)

Так как новые координаты точки 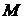есть

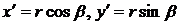, (4)

то из формул (3) получаем

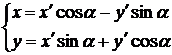(5)

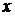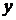Формулы (5) выражают старые координаты и точки 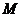через ее новые координаты 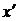и 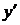. Чтобы выразить новые координаты 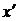и 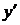через старые 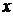и 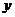, достаточно разрешить систему (5) относительно 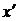и 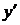. Но можно поступить проще: а именно, принять систему 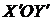за «старую», а систему XOY за «новую». Тогда, учитывая, что вторая система повернута относительно первой на угол 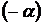, заменяя в формулах (5) 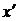и 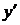соответственно на 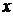и 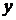, и обратно принимая во внимание, что 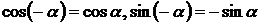, будем иметь

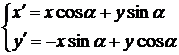
(6)

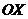Наконец, в общем случае, когда новое начало координат есть точка и ось образует с осью угол 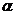, соединяя формулы (2) и (5), находим

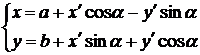(7)

Аналогично, из формул (1) и (6) получим

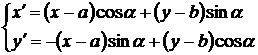
Вопрос 13. Кривые второго порядка.Каноническое уравнение эллипса.

Кривой 2-го порядка наз-ся множество точек в декартовой плоскости, которая удовлетворяет уравнению следущего вида:

Ах² + 2Вху + Су² + 2Dx + 2Ey + F = 0.

Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.

1) 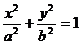- уравнение эллипса.

2) 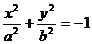- уравнение “мнимого” эллипса.

3) 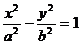- уравнение гиперболы.

4) y² = 2px – уравнение параболы.

5) y² – a² = 0 – уравнение двух параллельных прямых.

6) y² + a² = 0 – уравнение двух “мнимых” параллельных прямых.

7) y² = 0 – пара совпадающих прямых.

8) (x – a)² + (y – b)² = R² – уравнение окружности.

Эллипс.

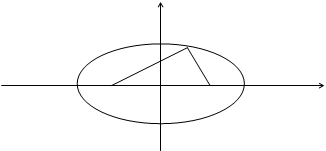
Определение.Эллипсом в каноническом виде наз-ся множество всех точек плоскости координаты которых удовлетворяют уравнению .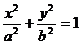

Определение.Фокусаминазываются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

M   М r1 r2 F1OF2

у

r1   М r1 r2 F1OF2

r2   М r1 r2 F1OF2

O   М r1 r2 F1OF2

x   М r1 r2 F1OF2

F2   М r1 r2 F1OF2

F1   М r1 r2 F1OF2

F₁, F₂ – фокусы. F₁ = (c; 0); F₂(-c; 0)

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема.Фокусное расстояние и полуоси эллипса связаны соотношением:

a² = b² + c².

откуда c=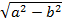

Определение.Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

Е = с/a.

Т.к. с<a, то е < 1.

Теорема.Для произвольной точки М(х, у), принадлежащей эллипсу верны соотношения:

r₁ = a – ex, r₂ = a + ex.

Доказательство.Выше было показано, что r₁ + r₂ = 2a. Кроме того, из геометрических соображений можно записать:

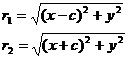
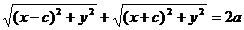
После возведения в квадрат и приведения подобных слагаемых:

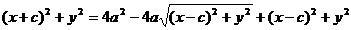
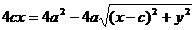
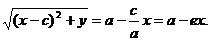
Аналогично доказывается, что r₂ = a + ex. Теорема доказана.

С эллипсом связаны две прямые, называемые директрисами. Их уравнения:

x = a/e; x = -a/e.

Отношение расстояния r_i от точки эллипса до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.

Доказательство.

Расстояния от точки М(х, у) до фокусов эллипса можно представить так:

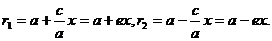Составим уравнения директрис:

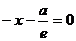(D₁), 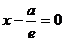(D₂). Тогда 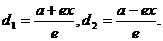Отсюда r_i/ d_i= e, что и требовалось доказать.

Теорема 2:

т. М принадлежит эллипсу 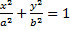не являющемуся окружностью, тогда и только тогда, когда отношение расстояния от М до фокуса к расстоянию от М до соответствующей этому фокусу директриссы равно эксцентриситету.

Доказательство:

Обозначим через l(L-малая) директриссу , расстояние от точки М (х,у) до данной директриссы равно 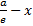, преобразуем 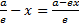, используя лемму получаем, что если точка М принадлежит эллипсу, то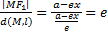

Достаточность пусть М(х,у) произвольная точка в плоскости, для которой выполняется:

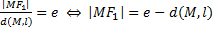по формулам длины отрезка: ,

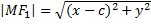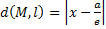возведем данное уравнение в квадрат:

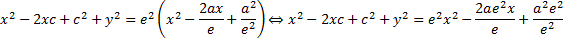
зная что ea=c, последнее равенство будет выглнядеть:

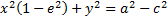, так как 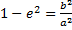, а 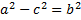в итоге получим:

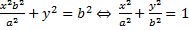таким образом точка М принадлежит эллипсу.

Вопрос 14. Кривые второго порядка.Каноническое уравнение параболы и гиперболы.

Гипербола.

Гиперболойназывается множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы: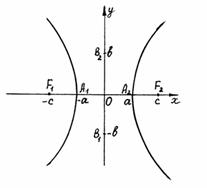

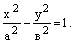Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

Ось 2а называется действительной осью гиперболы.

Ось 2b называется мнимой осью гиперболы.

Гипербола имеет две асимптоты, уравнения которых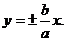

Определение.Отношение 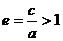называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с² – а² = b²:

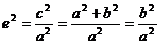
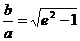
Если а = b, e = 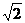, то гипербола называется равнобочной (равносторонней).

Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: .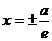

Свойства гиперболы:

1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (осьОх для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

2) Эксцентриситет гиперболы e> 1.

3)Отношение расстояния r_iот точки гиперболы до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.

Парабола.

Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки Fэтой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а прямая – ее директрисой.

y² = 2px ,Уравнение директрисы: x = -p/2.

называемомуканоническим уравнением параболы. Величина рназывается параметромпараболы.

Свойства параболы:

1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является осьОх, а вершиной – начало координат.

2) Вся парабола расположена в правой полуплоскости плоскости Оху.

Вопрос 15. Классификация кривых 2-го порядка.Приведение к каноническому виду.