Достаточные условия наличия точки перегиба.

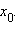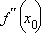Пусть функция f (x) непрерывна и имеет конечную или бесконечную производную в точке Если меняет знак при переходе через точку 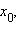то – то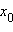чка перегиба функции f (x).

Если 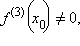то – то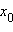чка перегиба функции f (x).

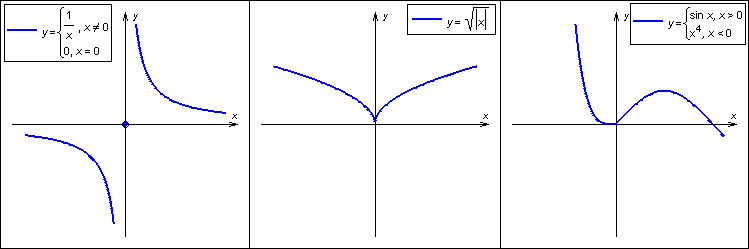
В заключение приведем примеры, когда точка x₀ не является точкой перегиба несмотря на то, что ее вторая производная меняет знак при переходе через эту точку:

если функция разрывна в точке 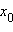(например );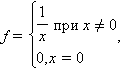

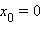в случае угловой точки (например,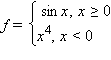

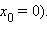
Не являются точками перегиба и точки возврата, например точка 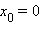у функции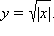

Все вышеперечисленные случаи изображены на рисунке.

График 3.2.3.2. Точки, не являющиеся точками перегиба: точка разрыва, точка возврата, угловая точка

Вопрос.

Вертикальная

Вертикальная асимптота — прямая вида 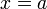при условии существования предела .

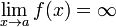Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

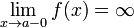
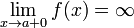
Замечание: обратите внимание на знаки бесконечностей в этих равенствах.

Горизонтальная

Горизонтальная асимптота — прямая вида 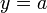при условии существования предела

.

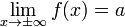Наклонная

Наклонная асимптота — прямая вида 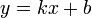при условии существования пределов

Пример наклонной асимптоты

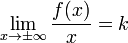
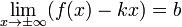
Замечание: функция может иметь не более двух наклонных(горизонтальных) асимптот!

Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен 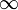), то наклонной асимптоты пр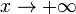и (или 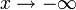) не существует!

Связь между наклонной и горизонтальной асимптотами

Если при вычислении предела 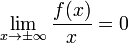, то очевидно, что наклонная асимптота совпадает с горизонтальной. Какова же связь между этими двумя видами асимптот?

Дело в том, что горизонтальная асимптота является частным случаем наклонной при 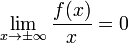, и из выше указанных замечаний следует, что

· Функция имеет или только одну наклонную асимптоту, или одну горизонтальную асимптоту, или одну наклонную и одну горизонтальную, или две наклонных, или две горизонтальных, либо же вовсе не имеет асимптот.

· Существование указанных в п. 1.) асимптот напрямую связано с существованием соответствующих пределов.

Нахождение асимптот

Порядок нахождения асимптот

Нахождение вертикальных асимптот.

Нахождение двух пределов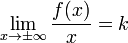

Нахождение двух пределов :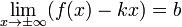

если 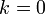в п. 2.), то 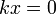, и предел 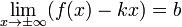ищется по формуле горизонтальной асимптоты, .

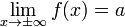Наклонная асимптота — выделение целой части

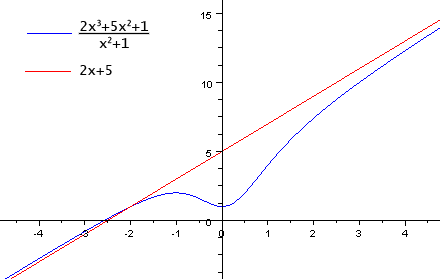
Также наклонную асимптоту можно найти, выделив целую часть. Например:

Дана функция .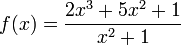

Разделив нацело числитель на знаменатель, получим:

.

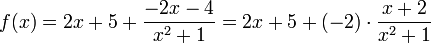При 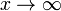, , 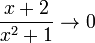то есть:

,

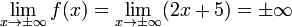и 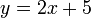является искомым уравнением асимптоты.

Вопрос.

Схема исследования функции.

7. Найти область определения функции.

8. Проверить, не является ли функция четной или нечетной; проверить также, не является ли она периодической.

9. Найти, если это возможно, точки пересечения графика функции с осями координат и промежутки знакопостоянства функции. Иногда для уточнения построения графика следует найти две три дополнительные точки.

10. Найти производную функции и ее критические точки.

11. Найти промежутки монотонности и экстремумы функции.

12. Построить график функции, используя полученные результаты исследования.

Схема нахождения наибольшего и наименьшего значений функции f(x), непрерывной на отрезке [a; b].

4. Найти значения функции в концах отрезка, т.е. f(a) и f(b) ;

5. Найти значения функции в тех критических точках, которые принадлежат интервалу (a,b) ;

6. Из найденных значений выбрать наибольшее и наименьшее.

Вопрос.