Основные тригонометрические тождества

o sin² α + cos² α = 1

o tg α · ctg α = 1

o tg α = sin α ÷ cos α

o ctg α = cos α ÷ sin α

o 1 + tg² α = 1 ÷ cos² α

o 1 + ctg² α = 1 ÷ sin² α

29.2

Если F(х) одна из первообразных для функции f(х) на промежутке J, то множество всех первообразных этой функции имеет вид: F(х)+С, где С - любое действительное число.

Доказательство:

Пусть F`(х) = f (х), тогда (F(х)+С)`= F`(х)+С`= f (х), для х Є J.
Допустим существует Φ(х)- другая первообразная для f (х) на промежутке J, т.е. Φ`(х) = f (х),
тогда (Φ(х)- F(х))` = f (х) – f (х) = 0, для х Є J.
Это означает, что Φ(х)- F(х) постоянна на промежутке J.
Следовательно, Φ(х)- F(х) = С.
Откуда Φ(х)= F(х)+С.
Это значит, что если F(х) - первообразная для функции f (х) на промежутке J, то множество всех первообразных этой функции имеет вид: F(х)+С, где С - любое действительное число.
Следовательно, любые две первообразные данной функции отличаются друг от друга постоянным слагаемым.

Функция 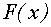называется первообразной для функции 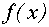, на заданном промежутке, если на этом промежутке функция 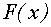непрерывна, и в каждой внутренней точке промежутка справедливо равенство:

.

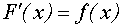Билет 30.1

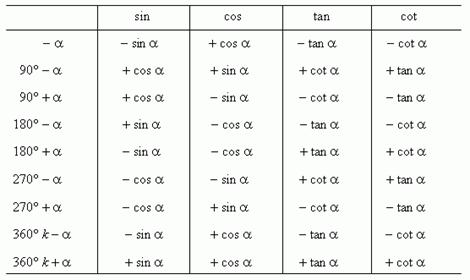
30.2

Билет 31.1

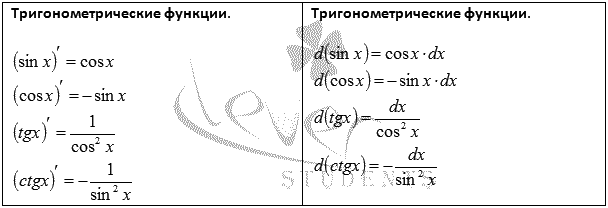
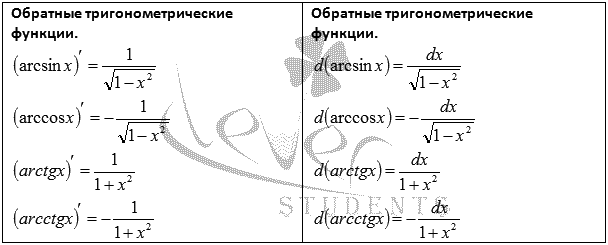
Итак, получили следующие формулы:

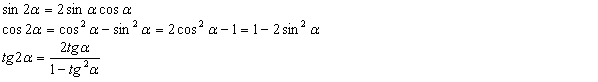
31.2

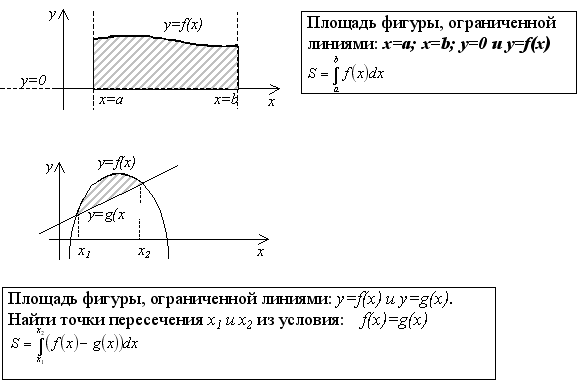
Интеграл функции — аналог суммы последовательности. Неформально говоря, (определённый) интеграл является площадью части графика функции (в пределах интегрирования), то есть площадью криволинейной трапеции.

Процесс нахождения интеграла называется интегрированием.

Согласно основной теореме анализа, интегрирование является операцией, обратной дифференцированию, чем помогает решатьдифференциальные уравнения.

. .

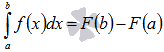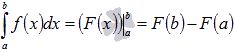Билет 32.1

sin (α + β) = sin α • cos β + sin β • cos α.

Синус суммы двух углов равен произведению синуса первого угла на косинус второго плюс произведение синуса второго угла на косинус первого.

Например,

sin 105° = sin (60° + 45°) = sin 60° • cos 45° + + sin45°.cos60° =

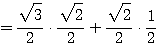
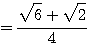
Формула (1) представляет собой тождество, то есть равенство, справедливое при любых значениях αиβ. В частности, оно должно быть верным, если β заменить на —β. В результате такой замены мы получим:

sin (α — β) = sin α • cos (— β) + sin (— β) • cos α. = sin α • cos β — sin β • cos α.

Итак,

sin (α — β) = sin α • cos β — sin β • cos α.(2)

Синус разности двух углов равен произведению синуса первого угла на косинус второго минус произведение синуса второго угла на косинус первого.

Например,

sin 15° = sin (45°—30°) = sin 45° • cos 30° — sin 30° • cos 45° =

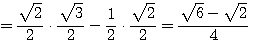
32.2

Криволинейной трапециейназывается фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a;b] функции f, осью Ox и прямыми x = a и x = b.

Билет 33.1

cos (α + β) = cos α cos β — sin α sin β, (1)

cos (α — β) = cos α cos β + sin α sin β. (2)

Косинус суммы (разности) двух углов равен произведению косинусов этих углов минус (плюс) произведение синусов этих углов

33.2

1. Находится область определения функции.

2. Находится производная.

3. Определяются критические точки.

4. Выбираются из критических точек те точки, которые принадлежат отрезку.

5. Считаются значения функции в критических точках принадлежащих отрезку и на концах отрезка.

Билет 34.1

Формулы сумма и разности синусов и косинусов выглядят следующим образом:

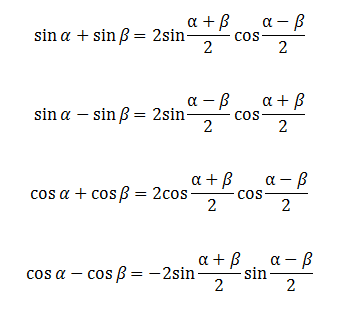
Билет 34.2

Билет 35.1

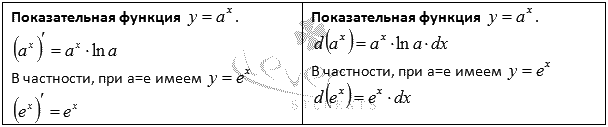
35.2