Произвольная усечённая пирамида
Формулы для усечённой пирамиды
Объём пирамиды 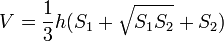 , где
, где 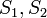 — площади оснований,
— площади оснований, 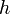 — высота усечённой пирамиды.
— высота усечённой пирамиды.
Площадь боковой поверхности 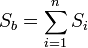 равна сумме площадей боковых граней усечённой пирамиды.
равна сумме площадей боковых граней усечённой пирамиды.
Формулы
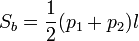 (Площадь боковой поверхности правильной усечённой пирамиды равна полупроизведению суммы периметров её оснований и апофемы)
(Площадь боковой поверхности правильной усечённой пирамиды равна полупроизведению суммы периметров её оснований и апофемы)
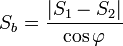 , где
, где 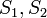 — площади оснований, а
— площади оснований, а 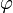 — двугранный угол при основании пирамиды.
— двугранный угол при основании пирамиды.
Билет 18.1
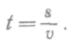
Скоростью равномерного движения называют отношение длины пути, пройденного телом, к промежутку времени, за который этот путь пройден:

скорость выразится формулой
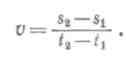
Зная скорость v равномерного движения, можно найти путь, пройденный за любой промежуток времени t, по формуле
s = vt.
Зная путь s, пройденный телом при равномерном движении, и скорость v этого движения, можно найти промежуток времени t, затраченный на прохождение этого пути, по формуле
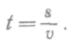
18.2
Определение: выпуклый многогранник называется правильным, если все его грани равные правильные многоугольники и, кроме того, в каждой вершине сходится одинаковое число ребер.
Существует всего 5 видов правильных многогранников:
Тетраэдр
Гексаэдр (Куб)
Октаэдр
Икосаэдр
Додекаэдр
Тетраэдрсоставлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Сумма плоских углов при каждой вершине равна 180 градусов. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.
Элементы симметрии:
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.
Радиус описанной сферы:
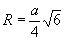
Радиус вписанной сферы:
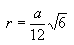
Площадь поверхности:
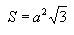
Объем тетраэдра:
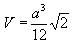
Кубсоставлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Сумма плоских углов при каждой вершине равна 270 градусов. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер.
Элементы симметрии:
Куб имеет центр симметрии - центр куба, 9 осей симметрии и 9 плоскостей симметрии.
Радиус описанной сферы:
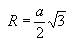
Радиус вписанной сферы:
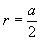
Площадь поверхности куба:
S=a2
Объем куба:
V=a3
Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной четырех треугольников. Сумма плоских углов при каждой вершине равна 240 градусов. Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер.
Элементы симметрии:
Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.
Радиус описанной сферы:
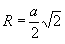
Радиус вписанной сферы:
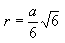
Площадь поверхности:
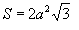
Объем октаэдра:
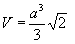
Икосаэдрсоставлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Сумма плоских углов при каждой вершине равна 300 градусов. Таким образом икосаэдр имеет 20 граней, 12 вершин и 30 ребер.
Элементы симметрии:
Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.
Радиус описанной сферы:
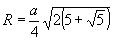
Радиус вписанной сферы:
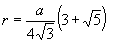
Площадь поверхности:
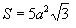
Объем икосаэдра:
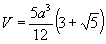
Додекаэдрсоставлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Сумма плоских углов при каждой вершине равна 324 градусов. Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.
Элементы симметрии:
Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.
Радиус описанной сферы:
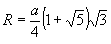
Радиус вписанной сферы:
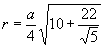
Площадь поверхности:
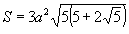
Объем додекаэдра:
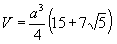
Билет 19.1
Каса́тельная пряма́я — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке 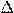 f=f(x0+
f=f(x0+ 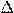 x)−f(x0)к приращению аргумента
x)−f(x0)к приращению аргумента 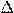 x
x
при 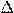 x
x 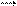 0: f
0: f  (x0)=lim
(x0)=lim 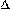 x
x 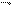 0
0  xf(x0+
xf(x0+  x)−f(x0).
x)−f(x0).
