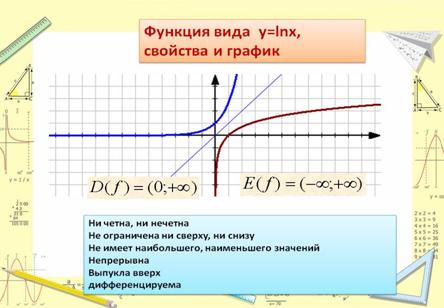
Свойства натурального логарифма
1. Область определения натурального логарифма 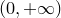 .
.
2. 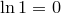 .
.
3. Натуральный логарифм – дифференцируемая функция, и 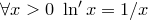 ,
, 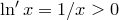 .
.
4. Натуральный логарифм строго возрастает, так как 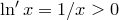 .
.
5. 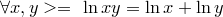 .
.
7.2
Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на эту плоскость. Пусть требуется найти расстояние от точки K до плоскости s (АВС).
Алгоритм построения:
|
Расстояние между параллельными плоскостями определяется длиной перпендикуляра, опущенного из произвольной точки одной плоскости до другой. Аналогично находится расстояние от плоскости до параллельной ей прямой. На прямой берется точка и находится расстояние до плоскости.
| Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра. Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость. | Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. |
| Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной. |
Билет 8.1
При a > 0, a 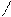 = 1, определена функция y = a x , отличная от постоянной. Эта функция называется показательной функцией с основанием a.
= 1, определена функция y = a x , отличная от постоянной. Эта функция называется показательной функцией с основанием a.
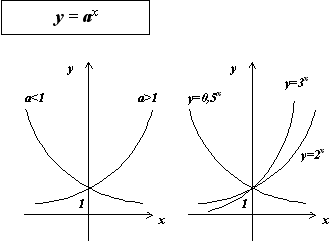
Основные свойства показательной функции y = a x при a > 1:
- Область определения функции - вся числовая прямая.
- Область значений функции - промежуток (0;+
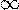 ).
). - Функция строго монотонно возрастает на всей числовой прямой, то есть, если x1< x2 , то ax1< ax2 .
- При x = 0 значение функции равно 1.
- Если x > 0 , то a x > 1 и если x < 0, то 0 < a < 1.
Графики показательных функций с основанием 0 < a < 1 и a > 1 изображены на рисунке.
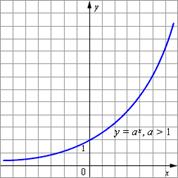 | 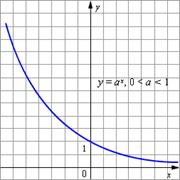 |
Основные свойства показательной функции y = a x при 0 < a < 1:
- Область определения функции - вся числовая прямая.
- Область значений функции - промежуток (0;+
 ).
). - Функция строго монотонно возрастает на всей числовой прямой, то есть, если x1< x2 , то ax1> ax2 .
- При x = 0 значение функции равно 1.
- Если x > 0 , то 0 < a < 1 и если x < 0, то a x > 1.
К общим свойствам показательной функции как при 0 < a < 1, так и при a > 1 относятся:
- ax1 ax2= ax1+ x2, для всех x1и x2.
- a−x=(ax)−1=1ax для любого x.
-
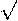 nax=axn для любого x и любого n
nax=axn для любого x и любого n 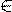 N
N  n
n 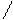 =1 .
=1 . - (ab)x = ax bx для любых a, b > 0; a,b
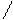 =1 .
=1 . - (ba)x=bxax для любых a, b > 0; a,b
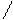 =1 .
=1 . - ax1 = ax2, то x1= x2.
8.2
| Теорема 4 О ТРЕХ ПЕРПЕНДИКУЛЯРАХ. Если прямая, проведенная на плоскости черезоснование наклонной, перпендикулярна еепроекции, то она перпендикулярна наклонной. И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной. | 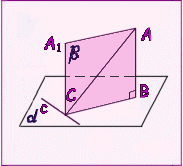 |
Доказательство: Пусть АВ - перпендикуляр плоскости 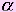 , АС - наклонная и с - прямая в плоскости , АС - наклонная и с - прямая в плоскости  , проходящая через основание С. Проведем прямую СA1, параллельную прямой АВ. Она перпендикулярна плоскости , проходящая через основание С. Проведем прямую СA1, параллельную прямой АВ. Она перпендикулярна плоскости  . Проведем через прямые АВ и СA1 плоскость . Проведем через прямые АВ и СA1 плоскость 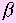 . Прямая сперпендикулярна прямой СA1. Если она перпендикулярна прямой СВ, то она перпендикулярна плоскости . Прямая сперпендикулярна прямой СA1. Если она перпендикулярна прямой СВ, то она перпендикулярна плоскости 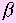 , а значит, и прямой АС. АНАЛОГИЧНО. Если прямая с перпендикулярна наклонной АС то она, будучи перпендикулярна и прямой СA1 перпендикулярна плоскости , а значит, и прямой АС. АНАЛОГИЧНО. Если прямая с перпендикулярна наклонной АС то она, будучи перпендикулярна и прямой СA1 перпендикулярна плоскости  , а значит, и проекции наклонной СВ. Теорема доказана. , а значит, и проекции наклонной СВ. Теорема доказана. |
Билет 9.1
На промежутке (0; +∞) определена функция, обратная к ax (a > 0, a ≠ 1). Эта функция называется логарифмической:
| y = loga x. |
Логарифмическая функция непрерывна и строго возрастает (если основание a > 1) или строго убывает (если 0 < a < 1) на всей области определения. Множество ее значений – все действительные числа.
Так как логарифмическая и показательная функции взаимно обратны, то при a > 0, a ≠ 1,
| |
| График 2.4.4.1. График логарифмической функции y = log2 x. |
|
Ниже приведены некоторые свойства логарифмов
(x > 0, 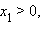
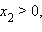 a > 0, a ≠ 1, b > 0, b ≠ 1,
a > 0, a ≠ 1, b > 0, b ≠ 1, 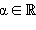 ).
).
|
9.2
Пусть прямая пересекает плоскость, причем не под прямым, а под каким-то другим углом. Такая прямая называется наклонной.
Опустим перпендикуляр из какой-либо точки наклонной на нашу плоскость. Соединим основание перпендикуляра с точкой пересечения наклонной и плоскости. Мы получилипроекцию наклонной на плоскость.
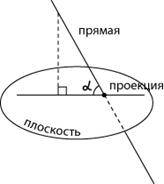
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.
Обратите внимание — в качестве угла между прямой и плоскостью мы выбираем острый угол.
Если прямая параллельна плоскости, значит, угол между прямой и плоскостью равен нулю.
Если прямая перпендикулярна плоскости, ее проекцией на плоскость окажется точка. Очевидно, в этом случае угол между прямой и плоскостью равен 90°.
Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
Это определение. Но как же с ним работать? Как проверить, что данная прямая перпендикулярна всем прямым, лежащим в плоскости? Ведь их там бесконечно много.
На практике применяется признак перпендикулярности прямой и плоскости:
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
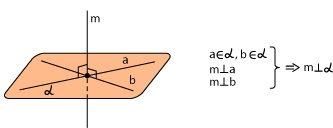
Билет 10.1
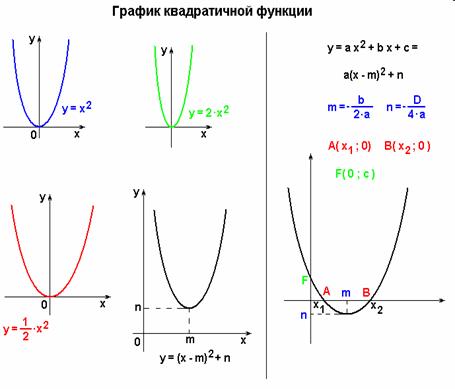
Функция, заданная формулой y = ax2 + bx + c , где x и y - переменные, а a, b, c - заданные числа, причем a 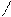 =0 , называется квадратичной функцией.
=0 , называется квадратичной функцией.
График квадратичной функции - парабола. Если a > 0 , то ветви параболы направлены вверх. Если a < 0 , то ветви параболы направлены вниз. График квадратичной функции называется параболой.
Любая квадратичная функция представима в виде 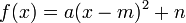 .
.
Координаты вершины параболы: 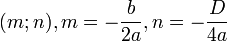 .
.
Прямая 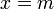 является осью симметрии графика квадратичной функции.
является осью симметрии графика квадратичной функции.
При 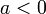 ветви параболы направлены вниз, при
ветви параболы направлены вниз, при 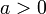 — вверх.
— вверх.
| Свойство | Дискриминант | ||
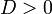 | 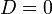 | 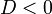 | |
| Область определения | 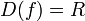 | ||
| Множество значений при a>0 | 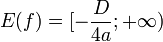 | ||
| Множество значений при a<0 | 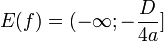 | ||
| Нули функции | 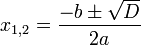 | 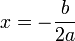 | 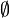 |
| Положительные (отрицательные) значения | 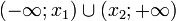 | Везде, кроме точки 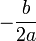 | Везде |
| Отрицательные (положительные) значения | 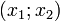 | Отсутствуют | |
| Промежуток убывания (возрастания) , если а>0 | 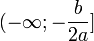 | ||
| Промежуток возрастания (убывания) , если a>0 | 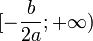 | ||
| Минимальное (максимальное) значение | 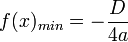 |
10.2
Двугранный угол — пространственная геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями
Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру. Таким образом, чтобы измерить двугранный угол, можно взять любую точку на его ребре и перпендикулярно ребру провести из неё лучи в каждую из граней. Линейный угол между этими двумя лучами и будет равен по величине двугранному углу. Если один из лучей не перпендикулярен ребру, то величина линейного угла между лучами в общем случае будет отлична от величины двугранного угла. Например, в любой двугранный угол (в том числе больший 90 градусов) можно поместить прямой угол так, чтобы его вершина лежала на ребре двугранного угла, а стороны принадлежали его граням. В этом легко убедиться, размещая угольник в приоткрытой книге.
У всякого многогранника, правильного или неправильного, выпуклого или вогнутого, есть двугранный угол на каждом ребре.
Величины двугранных углов правильных многогранников:
| Название | точный двугранный угол в радианах | приближённое значение в градусах |
| Тетраэдр | arccos(1/3) | 70.53° |
| Гексаэдр или куб | π/2 | 90°(точн.) |
| Октаэдр | π − arccos(1/3) | 109.47° |
| Додекаэдр | 2·arctg(φ) | 116.56° |
| Икосаэдр | 2·arctg(φ + 1) | 138.19° |
где φ = (1 + √5)/2 — золотое сечение.
Билет 11.1
Справедлива следующая теорема.
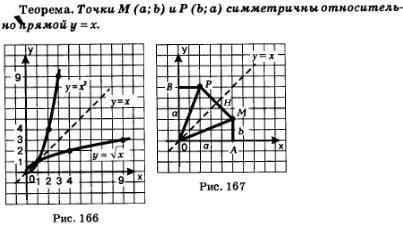
Доказательство. Будем считать для определенности, что а и b — положительные числа. Рассмотрим треугольники ОАМ и ОВР (рис. 167). Они равны, значит, ОР = ОМ и 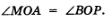 . Но тогда и
. Но тогда и 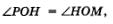 поскольку прямая у = х — биссектриса угла АОВ. Итак, треугольник РОМ — равнобедренный, ОН — его биссектриса, а значит, и ось симметрии. Точки М и Р симметричны относительно прямой ОН, что и требовалось доказать.
поскольку прямая у = х — биссектриса угла АОВ. Итак, треугольник РОМ — равнобедренный, ОН — его биссектриса, а значит, и ось симметрии. Точки М и Р симметричны относительно прямой ОН, что и требовалось доказать.
Итак, график функции 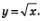 можно получить из графика функции у = х2, х>0 с помощью преобразования симметрии относительно прямой у = х. Аналогично график функции
можно получить из графика функции у = х2, х>0 с помощью преобразования симметрии относительно прямой у = х. Аналогично график функции 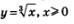 можно получить из графика функции у = х3, х> 0 с помощью преобразования симметрии относительно прямой у=х; график функции
можно получить из графика функции у = х3, х> 0 с помощью преобразования симметрии относительно прямой у=х; график функции 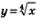 можно получить из графика функции
можно получить из графика функции 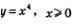 с помощью преобразования симметрии относительно прямой у = х и т.д. Напомним, что график функции
с помощью преобразования симметрии относительно прямой у = х и т.д. Напомним, что график функции 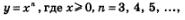 напоминает по виду ветвь параболы
напоминает по виду ветвь параболы 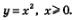 Чем больше п, тем круче эта ветвь устремляется вверх на промежутке
Чем больше п, тем круче эта ветвь устремляется вверх на промежутке 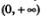 и тем ближе подходит к оси х в окрестности точки х=0 (рис. 168).
и тем ближе подходит к оси х в окрестности точки х=0 (рис. 168).
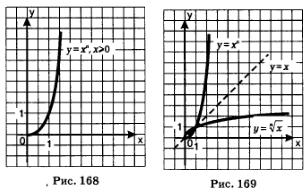
Сформулируем общий вывод: график функции 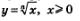 симметричен графику функции
симметричен графику функции 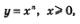 , относительно прямой у = х(рис. 169).
, относительно прямой у = х(рис. 169).
Свойства функции 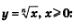
1) 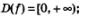
2) функция не является ни четной, ни нечетной;
3) возрастает на 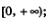
4) не ограничена сверху, ограничена снизу;
5) не имеет наибольшего значения; 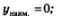
6) непрерывна;
7) 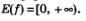
11.2
| Теорема 5 ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ. Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны. | 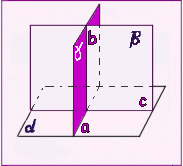 |
Доказательство: Пусть 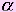 - плоскость , b - перпендикулярная ей прямая, - плоскость , b - перпендикулярная ей прямая, 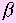 - плоскость проходящая через прямую b, и с - прямая по которой пересекаются плоскости - плоскость проходящая через прямую b, и с - прямая по которой пересекаются плоскости 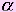 и и 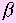 . Докажем, что плоскости . Докажем, что плоскости 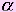 и и 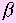 перпендикулярны. Проведем в плоскости перпендикулярны. Проведем в плоскости 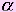 через точку пересечения прямой b с плоскостью через точку пересечения прямой b с плоскостью 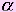 прямую а, перпендикулярную прямой с. Проведем через прямые а и bплоскость прямую а, перпендикулярную прямой с. Проведем через прямые а и bплоскость 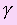 . Она перпендикулярна прямой с, так как прямые а и bперпендикулярны, то плоскости . Она перпендикулярна прямой с, так как прямые а и bперпендикулярны, то плоскости 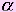 и и 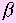 перпендикулярны. Теорема доказана. перпендикулярны. Теорема доказана. | |
Билет12.1

12.2
Параллелепипед — это четырехугольная призма, все грани которой — параллелограммы.
Параллелепипеды, как и призмы, могут быть прямыми и наклонными.
Прямой параллелепипед, основанием которого служит прямоугольник, называют прямоугольным параллелепипедом.
У прямоугольного параллелепипеда все грани — прямоугольники.
Длины трёх ребер прямоугольного параллелепипеда, имеющих общий конец, называют его измерениями.
Куб— прямоугольный параллелепипед с равными измерениями.
Все шесть граней куба — равные квадраты.
· Параллелепипед симметричен относительно середины его диагонали.
· Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
· Противолежащие грани параллелепипеда параллельны и равны.
· Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений

В параллелепипеде:
1) противолежащие грани равны и параллельны;
2) все четыре диагонали пересекаются в одной точке и делятся в ней пополам.
Доказательства:
1) Для любой пары противолежащих граней параллелепипеда имеем: соответствующие углы равны (например, 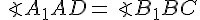 ,
, 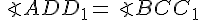 и т. д.); соответствующие стороны равны и параллельны (
и т. д.); соответствующие стороны равны и параллельны ( 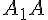 и
и 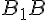 ,
, 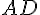 и
и 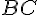 и т. д. как противолежащие стороны параллелограммов). Отсюда
и т. д. как противолежащие стороны параллелограммов). Отсюда 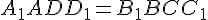 и их плоскости параллельны.
и их плоскости параллельны.
2) 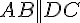 и
и 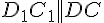 , поэтому
, поэтому 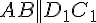 . Через
. Через 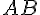 и
и 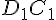 проведем плоскость, тогда
проведем плоскость, тогда 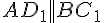 .
. 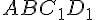 — параллелограмм. Его диагонали
— параллелограмм. Его диагонали 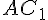 и
и 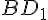 , являющиеся диагоналями параллелепипеда, в точке пересечения делятся пополам. Теперь возьмем одну из этих диагоналей, например
, являющиеся диагоналями параллелепипеда, в точке пересечения делятся пополам. Теперь возьмем одну из этих диагоналей, например 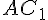 и третью диагональ параллелепипеда
и третью диагональ параллелепипеда 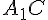 . Они являются диагоналями параллелограмма
. Они являются диагоналями параллелограмма 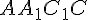 и поэтому
и поэтому 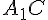 проходит через середину
проходит через середину 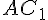 , т. е. три диагонали параллелепипеда пересекаются в одной точке и делятся в ней пополам. Аналогично доказывается и для четвертой диагонали
, т. е. три диагонали параллелепипеда пересекаются в одной точке и делятся в ней пополам. Аналогично доказывается и для четвертой диагонали 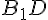 .
.
Теорема 3
В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений (т. е. трех ребер, выходящих из одной вершины).
Следствие
В прямоугольном параллелепипеде все диагонали равны.
Билет 13.1
Простейшими называются тригонометрические уравнения следующих четырёх видов:
sin x = a; cos x = a; tg x = a; ctg x = a:
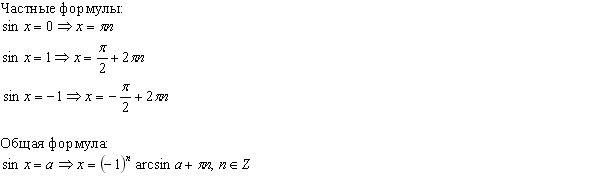

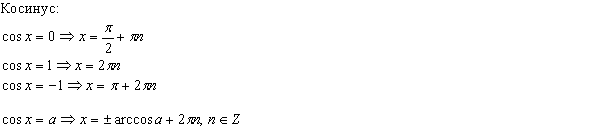
Общий вид решения уравнения tg x = a определяется формулой:
x = arctg(a) + pk, k Î Z (целые числа).
Общий вид решения уравнения ctg x = a определяется формулой:
x = arcctg(a) + pk, k Î Z (целые числа).
| Уравнение: | Уравнение: | РЕШЕНИЯ: |
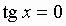 | *** | 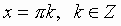 |
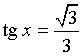 | 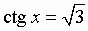 | 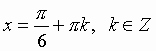 |
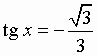 | 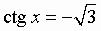 | 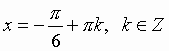 |
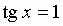 | 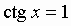 | 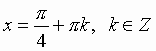 |
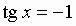 | 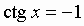 | 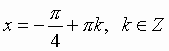 |
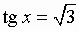 | 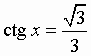 | 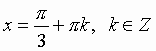 |
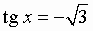 | 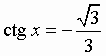 | 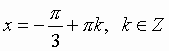 |
| *** | 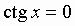 | 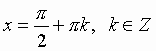 |
13.2
Призма — многогранник, две грани которого являются конгруэнтными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.
Призмы бывают прямые и наклонны
Боковые грани правильной призмы являются равными прямоугольниками.
Боковые ребра правильной призмы равны.
Правильная призма является прямой.
Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником.
§ Основания призмы являются равными многоугольниками.
§ Боковые грани призмы являются параллелограммами.
§ Боковые ребра призмы параллельны и равны.
§ Объём призмы равен произведению её высоты на площадь основания:
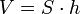
§ Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
§ Площадь боковой поверхности произвольной призмы 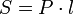 , где
, где 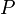 — периметр перпендикулярного сечения,
— периметр перпендикулярного сечения, 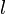 — длина бокового ребра.
— длина бокового ребра.
§ Площадь боковой поверхности правильной призмы 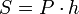 , где
, где 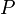 — периметр основания призмы, ,
— периметр основания призмы, , 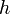 — высота призмы.
— высота призмы.
§ Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы.
§ Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах.
§ Перпендикулярное сечение перпендикулярно ко всем боковым граням.
Формула
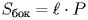
Строгая формулировка
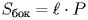
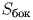 - площадь боковой поверхности призмы;
- площадь боковой поверхности призмы;
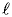 - длина бокового ребра;
- длина бокового ребра;
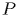 - периметр сечения призмы плоскостью, перпендикулярной боковым ребрам (сечение должно пересекать все боковые грани призмы).
- периметр сечения призмы плоскостью, перпендикулярной боковым ребрам (сечение должно пересекать все боковые грани призмы).
Билет 14.1

 h1, m2
h1, m2 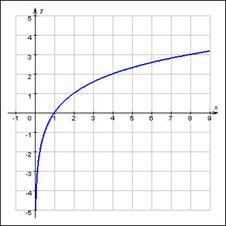
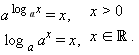
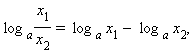
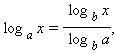
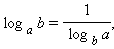
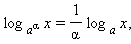 α ≠ 0.
α ≠ 0.