Признак скрещивающихся прямых.
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x1; y1; z1) и b = (x2; y2; z2), то сможете найти угол. Точнее, косинус угла по формуле:
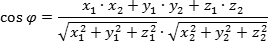
Билет 4.1
Логарифм числа b по основанию a (logab) определяется как показатель степени, в которую надо возвести число a, чтобы получить число b (Логарифм существует только у положительных чисел).
Обозначение: logab.
logab = x, ax = b.
Логарифм числа b по основанию a - logab (a > 0, a ≠ 1, b > 0)
Десятичный логарифм - lg b (Логарифм по основанию 10, а = 10).
Натуральный логарифм - ln b (Логарифм по основанию e, а = e).
Формулы и свойства логарифмов
1° Основное логарифмическое тождество - alogab = b;
2° loga1 = 0;
3° logaa = 1;
4° loga(bc) = logab + logac;
5° loga(b/c) = logab - logac;
6° loga(1/c) = loga1 - logac = - logac;
7° loga(bc) = c logab;
8° log(ac)b = (1/c) logab;
4.2
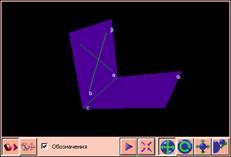
| Теорема Если стороны двух углов соответственно сонаправлены, то такие углы равны. |
Рассмотрим углы О и О1 с соответственно сонаправленными сторонами и докажем, что угол O равен углу O1.
Отметим на сторонах угла О какие-нибудь точки А и В и отложим на соответственных сторонах угла О1отрезки О1А1=ОА и 01В1=ОВ (рис. 25).
Четырехугольник ОО1А1А — параллелограмм, так как противоположные стороны OA и O1A1параллельны и равны. Отсюда следует, что АА1||001 и AA1=OO1. Аналогично четырехугольник OO1BB1 — параллелограмм, поэтому ВВ1||001 и ВВ1=ОО1 Так как АА1||ОО1 и BBl||001, то по теореме о трех параллельных прямых АА1||ВВ1. Кроме того, АА1=001=ВВ1. Таким образом, в четырехугольнике АВВ1А1противоположные стороны АА1 и ВВ1 параллельны и равны. Следовательно, этот четырехугольник — параллелограмм, и значит, стороны АВ и А1В1 равны.
Сравним теперь треугольники АОВ и A1O1B1. Они равны по трем сторонам, и поэтому угол O равен углу O1 Теорема доказана.
Билет 5.1
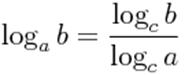
5.2
Определение 2.5.
Две плоскости называются параллельными, если они не имеют общих точек.
Теорема 2.6. Признак параллельности плоскостей.
Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны.
Доказательство проведем от противного. Пусть прямые a и b лежат в плоскости β, причем a || α и b || α (чертеж 2.3.1). Если плоскости α и β не параллельны, то они пересекаются по некоторой прямой c. Поскольку a || α, то по теореме о следе c || a. Аналогично получаем, что c || b, тогда a || b. Мы пришли к противоречию, поскольку a и b по условию пересекаются. |
Теорема 2.7.
Если две параллельные плоскости пересечены третьей, то она оставляет на этих плоскостях параллельные следы.
| |
Теорема 2.8.
Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.
Теорема 2.9.
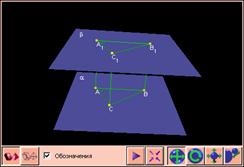
Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны.
| |
| Чертеж 2.3.3. |
Теорема 2.10.
Два угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях.
На чертеже 2.3.4 показаны углы BAC и B1A1C1, причем AB || A1B1 и AC || A1C1. По признаку параллельности плоскостей плоскость BAC параллельна плоскостиB1A1C1. Пусть соответствующие отрезки на сторонах угла равны: AB = A1B1 и AC = A1C1. Проведем прямые AA1, BB1, CC1. Четырехугольник ABB1A1 – параллелограмм, так как AB = A1B1 и AB || A1B1, следовательно, AA1 = BB1 и AA1 || BB1. Аналогично докажем, что AA1 = CC1. Отсюда следует, что BB1 = CC1 и BB1 || CC1, следовательно, CBB1C1 – параллелограмм и CB = C1B1. Теперь утверждаем, что Δ ABC = Δ A1B1C1, откуда |
Билет 6.1
Логарифмы по основанию 10 (обозначение: 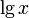 ) до изобретения калькуляторов широко применялись для вычислений. Они обладали преимуществом перед логарифмами с иным основанием: целую часть
) до изобретения калькуляторов широко применялись для вычислений. Они обладали преимуществом перед логарифмами с иным основанием: целую часть  логарифма числа
логарифма числа 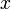 легко определить.
легко определить.
§ Если 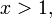 то
то 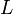 на 1 меньше числа цифр в целой части числа
на 1 меньше числа цифр в целой части числа 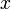 . Например, сразу очевидно, что
. Например, сразу очевидно, что 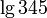 находится в промежутке
находится в промежутке 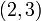 .
.
§ Если 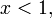 то ближайшее к
то ближайшее к  целое (в меньшую сторону) равно общему числу нулей в
целое (в меньшую сторону) равно общему числу нулей в 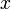 перед первой ненулевой цифрой, взятому со знаком минус. Например,
перед первой ненулевой цифрой, взятому со знаком минус. Например, 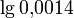 находится в интервале
находится в интервале 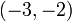 .
.
Кроме того, при переносе десятичной запятой в числе на 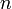 разрядов значение десятичного логарифма этого числа изменяется на
разрядов значение десятичного логарифма этого числа изменяется на 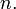 Например,
Например, 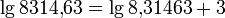 . Отсюда следует, что достаточно составить таблицу десятичных логарифмов для чисел в диапазоне от
. Отсюда следует, что достаточно составить таблицу десятичных логарифмов для чисел в диапазоне от 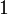 до
до 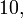 причём привести в таблице только мантиссы (дробную часть) логарифмов.
причём привести в таблице только мантиссы (дробную часть) логарифмов.
Связь с натуральным логарифмом:

Поскольку применение логарифмов для расчётов с появлением вычислительной техники почти прекратилось, в наши дни десятичный логарифм в значительной степени вытеснен натуральным. Он сохраняется в основном в тех математических моделях, где исторически укоренился — например, при построении логарифмических шкал.
y = lg(x) - десятичный логарифм от х
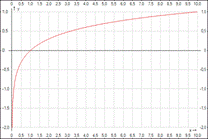
Текст формулы:
y(x) =
y = lg(1/2)(x) - корень квадратный от десятичного логарифма от x
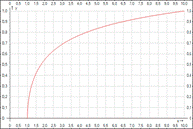
Текст формулы:
y(x) =
y = lg(x+1)lg(x+2) - произведение десятичных логарифмов
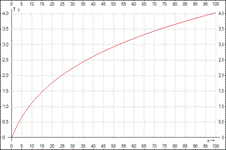
Текст формулы:
y(x) =
y = lg(x^2) - десятичный логарифм от квадрата x
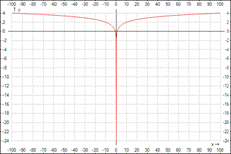
Текст формулы:
y(x) =
6.2
Определение
Прямая, пересекающая плоскость, перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку называется перпендикулярной этой плоскости, если она пересечения.
Теорема 1
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ.
Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
Теорема 2
1-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ.
Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой
Теорема 3
2-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ.
Две прямые, перпендикулярные одной и той же плоскости, параллельны.
Билет 7.1
Теорема. Пусть 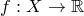 ,
, 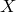 – промежуток, функция
– промежуток, функция 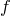 непрерывна. Тогда у функции
непрерывна. Тогда у функции 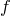 есть первообразная.
есть первообразная.
Рассмотрим функцию 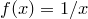 на промежутке
на промежутке 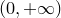 . По предыдущей теореме, эа функция имеет первообразную. Все первообразные ее имеют вид
. По предыдущей теореме, эа функция имеет первообразную. Все первообразные ее имеют вид 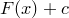 . Выберем из всех этих первообразных такую, значение которой при
. Выберем из всех этих первообразных такую, значение которой при 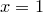 равно
равно 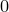 . Такая первообразная найдется (почему?). Назовем ее натуральным логарифмом.
. Такая первообразная найдется (почему?). Назовем ее натуральным логарифмом.
Обозначение: 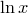 .
.

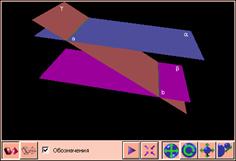 Пусть α и β параллельны, γ – третья плоскость, которая пересекает их, причем α
Пусть α и β параллельны, γ – третья плоскость, которая пересекает их, причем α  γ = a, β
γ = a, β 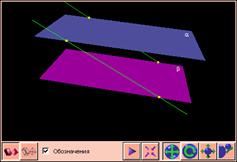
 BAC =
BAC =