Геометрический и механический смысл первой производной.
Производная. Рассмотрим некоторую функцию y = f ( x ) в двух точках x0 и x0 + 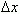 : f ( x0 ) и f ( x0 +
: f ( x0 ) и f ( x0 + 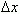 ). Здесь через
). Здесь через 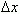 обозначено некотороемалое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции: f ( x0 +
обозначено некотороемалое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции: f ( x0 + 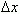 ) - f ( x0)называется приращением функции. Производной функции y = f ( x ) в точке x0называется предел:
) - f ( x0)называется приращением функции. Производной функции y = f ( x ) в точке x0называется предел:
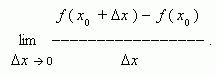
Если этот предел существует, то функция f ( x ) называется дифференцируемой в точке x0 . Производная функции f ( x ) обозначается так:
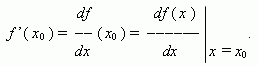
Геометрический смысл производной. Рассмотрим график функции y = f ( x ):
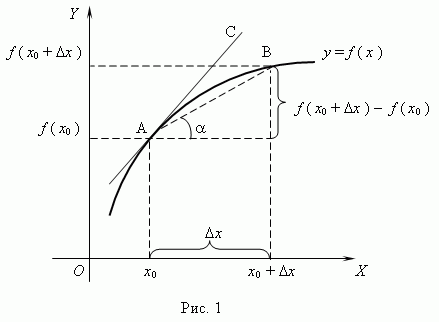
Из рис.1 видно, что для любых двух точек A и B графика функции:
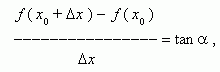
где 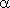 - угол наклона секущей AB.
- угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точкуB, то 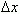 неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.
неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.
Уравнение касательной. Выведем уравнение касательной к графику функции в точке A ( x0 , f ( x0) ). В общем случае уравнение прямой с угловым коэффициентом f ’( x0) имеет вид:
y = f ’( x0) · x + b .
Чтобы найти b,воспользуемся тем, что касательная проходит через точку A:
f ( x0) = f ’( x0) · x0 + b ,
отсюда, b = f ( x0) – f ’( x0) · x0, и подставляя это выражение вместо b, мы получим уравнение касательной:
y = f ( x0) + f ’( x0) · ( x – x0) .
Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x ( t ) времени t. В течение интервала времени от t0 до t0 + 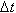 точка перемещается на расстояние: x ( t0 +
точка перемещается на расстояние: x ( t0 + 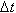 ) - x ( t0 ) =
) - x ( t0 ) = 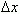 , а её средняя скорость равна: va =
, а её средняя скорость равна: va = 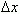 /
/ 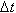 . При
. При 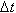
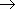 0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v ( t0) материальной точки в момент времени t0 . Но по определению производной мы имеем:
0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v ( t0) материальной точки в момент времени t0 . Но по определению производной мы имеем:
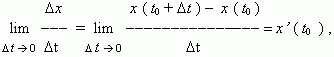
отсюда, v ( t0) = x’ ( t0) , т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной.Аналогично, ускорение – это производная скорости по времени: a = v’ ( t ).
Примеры задач
Задача 1. Составьте уравнение общей касательной к графикам функций 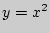 и
и 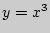 .
.
Решение.
I способ.
Прямая 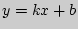 является общей касательной графиков функций
является общей касательной графиков функций 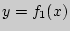 и
и 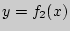 , если она касается как одного, так и другого графиков, но совершенно не обязательно в одной и той же точке.
, если она касается как одного, так и другого графиков, но совершенно не обязательно в одной и той же точке.
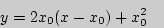 - уравнение касательной к графику функции y=x2 в точке с абсциссой x0
- уравнение касательной к графику функции y=x2 в точке с абсциссой x0
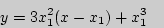 - уравнение касательной к графику функции y=x3 в точке с абсциссой x1
- уравнение касательной к графику функции y=x3 в точке с абсциссой x1
Прямые совпадают, если их угловые коэффициенты и свободные члены равны. Отсюда
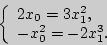
Решением системы будут

Уравнения общих касательных имеют вид:
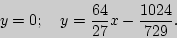
16. Правила дифференцирования. Производные сложной, обратной и неявной функции.
Правила дифференцирования
При дифференцировании константу можно выносить за производную:
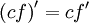
Правило дифференцирования суммы функций:
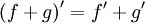
Правило дифференцирования разности функций:
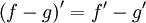
Правило дифференцирования произведения функций (правило Лейбница):
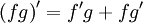
Правило дифференцирования частного функций:
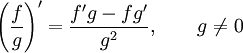
Правило дифференцирования функции в степени другой функции:
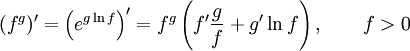
Правило дифференцирования сложной функции:
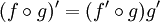
Правило логарифма при дифференцировании функции:
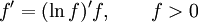
| Производная сложной функции |
"Двухслойная" сложная функция записывается в виде 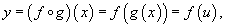 где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция 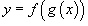 также дифференцируема по x и ее производная равна также дифференцируема по x и ее производная равна 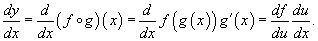 Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)! Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга. Рассмотрим несколько примеров, иллюстрирующих правило производной сложной функции. Это правило широко применяется и во многих других задачах раздела "Дифференцирование". Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)! Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга. Рассмотрим несколько примеров, иллюстрирующих правило производной сложной функции. Это правило широко применяется и во многих других задачах раздела "Дифференцирование". |
| Пример 1 |
Найти производную функции 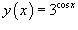 . Решение. Поскольку . Решение. Поскольку 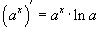 , то по правилу производной сложной функции получаем , то по правилу производной сложной функции получаем 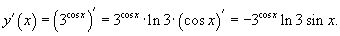 |
