Точки разрыва первого и второго рода
Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
· если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;
· если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.
Свойства:
Локальные
· Функция, непрерывная в точке 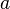 , является ограниченной в некоторой окрестности этой точки.
, является ограниченной в некоторой окрестности этой точки.
· Если функция 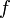 непрерывна в точке
непрерывна в точке 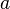 и
и 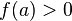 (или
(или 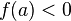 ), то
), то 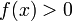 (или
(или 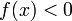 ) для всех
) для всех 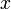 , достаточно близких к
, достаточно близких к 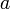 .
.
· Если функции 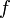 и
и 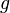 непрерывны в точке
непрерывны в точке 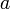 , то функции
, то функции 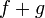 и
и 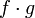 тоже непрерывны в точке
тоже непрерывны в точке 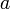 .
.
· Если функции 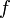 и
и 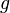 непрерывны в точке
непрерывны в точке 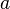 и при этом
и при этом 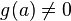 , то функция
, то функция 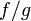 тоже непрерывна в точке
тоже непрерывна в точке 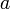 .
.
· Если функция 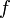 непрерывна в точке
непрерывна в точке 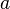 и функция
и функция 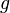 непрерывна в точке
непрерывна в точке 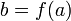 , то их композиция
, то их композиция 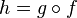 непрерывна в точке
непрерывна в точке 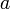 .
.
Глобальные
· Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
· Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
· Областью значений функции 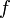 , непрерывной на отрезке
, непрерывной на отрезке 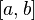 , является отрезок
, является отрезок 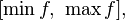 где минимум и максимум берутся по отрезку
где минимум и максимум берутся по отрезку 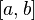 .
.
· Если функция 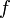 непрерывна на отрезке
непрерывна на отрезке 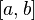 и
и 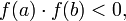 то существует точка
то существует точка 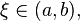 в которой
в которой 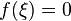 .
.
· Если функция 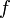 непрерывна на отрезке
непрерывна на отрезке 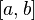 и число
и число 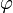 удовлетворяет неравенству
удовлетворяет неравенству 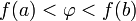 или неравенству
или неравенству 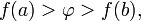 то существует точка
то существует точка 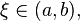 в которой
в которой 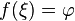 .
.
· Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
· Монотонная функция на отрезке 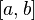 непрерывна в том и только в том случае, когда область ее значений является отрезком с концами
непрерывна в том и только в том случае, когда область ее значений является отрезком с концами 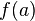 и
и 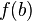 .
.
· Если функции 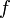 и
и 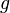 непрерывны на отрезке
непрерывны на отрезке 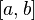 , причем
, причем 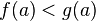 и
и 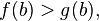 то существует точка
то существует точка 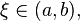 в которой
в которой 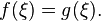 Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
Производные и дифференциалы высших порядков
· Производной от функции называется конечный предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
· 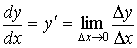 , или
, или 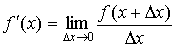 .
.
· Геометрически производная представляет собой угловой коэффициент касательной к графику функции 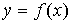 в точке х, то есть .
в точке х, то есть . 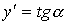
· Производная есть скорость изменения функции в точке х.
· Отыскание производной называется дифференцированием функции.
· Формулы дифференцирования основных функций:
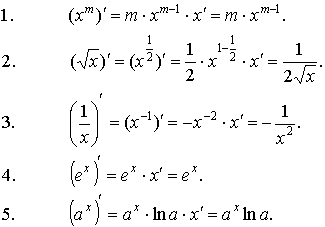
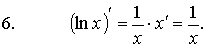
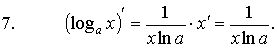
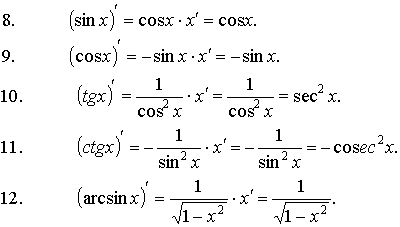
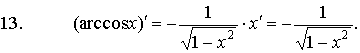
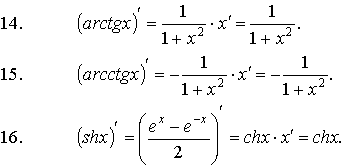
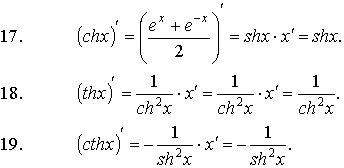 | |
3. Основные правила дифференцирования
Пусть 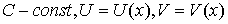 , тогда:
, тогда:
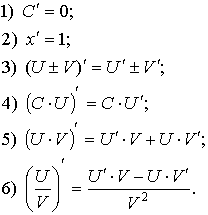
7) Если 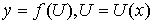 , то есть
, то есть 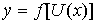 , где
, где 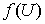 и
и 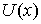 имеют производные, то
имеют производные, то 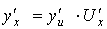 (правило дифференцирования сложной функции).
(правило дифференцирования сложной функции).
Примеры:
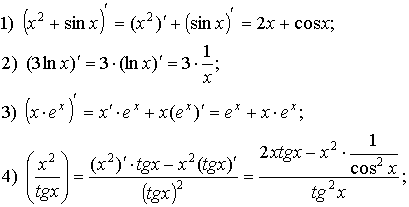
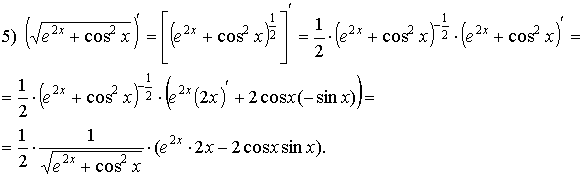
Производные высших порядков
Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производнойфункции f и обозначается f". Таким образом,
f"(x) = (f'(x))'.
Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f(n). Итак,
f(n)(x) = (f(n-1)(x))', n ϵ N, f(0)(x) = f(x).
Число n называется порядком производной.
Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом,
dnf(x) = d(dn-1f(x)), d0f(x) = f(x), n ϵ N.
Если x - независимая переменная, то
dx = const и d2x = d3x = ... = dnx = 0.
В этом случае справедлива формула
dnf(x) = f(n)(x)(dx)n.
