Определитель третьего порядка
Определителем третьего порядка называется следующее выражение: 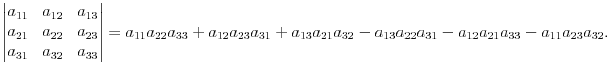
Определитель третьего порядка вычислить легко, если учесть следующее правило: со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной в противоположого угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольноков, построенных относительно этой диагонали. Следующая схема демонстрирует это правило, называемое правилом треугольников. В схеме синим (слева) отмечены элементы, чьи произведения идут со знаком плюс, а зеленым (справа) - со знаком минус. 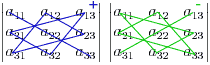
Определитель второго порядка вычисляется по формуле
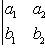
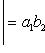
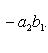
Определитель третьего порядка вычисляется по формуле
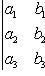
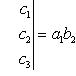
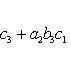
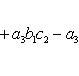
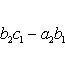
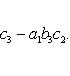
Определители более высоких порядков.
Минором Mij элемента aij (i,j=1,n) называется определитель (n-1)-го порядка, полученный из определителя n-го порядка, вычерчиванием i-й строки и j-го столбца. Алгебраическое дополнение Aij элемента Aij определяется равенством
Aij=(-1)i+j Mij
Для произвольного натурального числа (теорема Лапласа, разложение по i-строке)
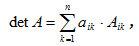
Векторы и действие над ними. Действие над векторами, заданными своими координатами.
Определение 3. Модульвектора – это длина отрезка AB.
Определение 4.Вектор, модуль которого равен нулю, называется нулевым, обозначается 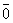 .
.
Определение 5.Векторы, расположенные на параллельных прямых или на одной прямой называются коллинеарными. Если два коллинеарных вектора имеют одинаковое направление, то они называются сонаправленными.
Определение 6.Два вектора считаются равными, если они сонаправлены и равны по модулю.
Действия над векторами.
Сложение векторов.
Опр. 6. Суммой двух векторов  и
и  является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма).
является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма).
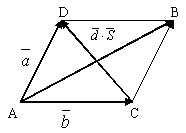
Рис.1.
Опр. 7.Суммойтрех векторов  ,
,  ,
, 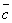 называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
Опр. 8.Если А, В, С – произвольные точки, то 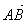 +
+ 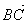 =
= 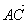 (правило треугольника).
(правило треугольника).
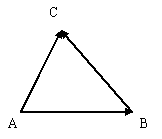
рис.2
Свойства сложения.
1о.  +
+  =
=  +
+  (переместительный закон).
(переместительный закон).
2о.  + (
+ (  +
+ 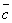 ) = (
) = (  +
+  ) +
) + 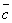 = (
= (  +
+ 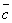 ) +
) +  (сочетательный закон).
(сочетательный закон).
3о.  + (–
+ (–  ) +
) + 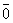 .
.
Вычитание векторов.
Опр. 9.Подразностью векторов  и
и  понимают вектор
понимают вектор 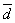 =
=  –
–  такой, что
такой, что  +
+ 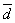 =
=  .
.
В параллелограмме – это другая диагональ СД (см.рис.1).
Умножение вектора на число.
Опр. 10. Произведением вектора  на скаляр k называется вектор
на скаляр k называется вектор
 = k
= k  =
=  k,
k,
имеющий длину ka, и направление, которого:
1. совпадает с направлением вектора  , если k > 0;
, если k > 0;
2. противоположно направлению вектора  , если k < 0;
, если k < 0;
3. произвольно, если k = 0.
Свойства умножения вектора на число.
1о. (k + l)  = k
= k  + l
+ l  .
.
k(  +
+  ) = k
) = k  + k
+ k  .
.
2o. k(l  ) = (kl)
) = (kl)  .
.
3o. 1×  =
=  , (–1) ×
, (–1) ×  = –
= –  , 0 ×
, 0 ×  =
= 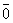 .
.
Действия над векторами.
Сложение векторов.
Опр. 6. Суммой двух векторов  и
и  является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма).
является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма).
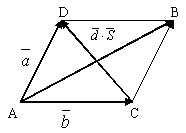
Рис.1.
Опр. 7.Суммойтрех векторов  ,
,  ,
, 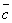 называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
Опр. 8.Если А, В, С – произвольные точки, то 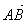 +
+ 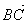 =
= 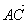 (правило треугольника).
(правило треугольника).
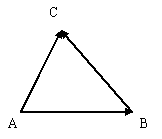
рис.2
Свойства сложения.
1о.  +
+  =
=  +
+  (переместительный закон).
(переместительный закон).
2о.  + (
+ (  +
+ 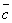 ) = (
) = (  +
+  ) +
) + 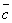 = (
= (  +
+ 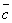 ) +
) +  (сочетательный закон).
(сочетательный закон).
3о.  + (–
+ (–  ) +
) + 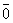 .
.
Вычитание векторов.
Опр. 9.Подразностью векторов  и
и  понимают вектор
понимают вектор 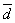 =
=  –
–  такой, что
такой, что  +
+ 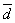 =
=  .
.
В параллелограмме – это другая диагональ СД (см.рис.1).
Умножение вектора на число.
Опр. 10. Произведением вектора  на скаляр k называется вектор
на скаляр k называется вектор
 = k
= k  =
=  k,
k,
имеющий длину ka, и направление, которого:
1. совпадает с направлением вектора  , если k > 0;
, если k > 0;
2. противоположно направлению вектора  , если k < 0;
, если k < 0;
3. произвольно, если k = 0.
