Дифференциал высшего порядка функции одной переменной

Для функции, зависящей от одной переменной 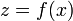второй и третий дифференциалы выглядят так:

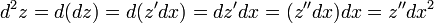
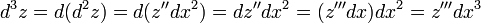
Отсюда можно вывести общий вид дифференциала n-го порядка от функции :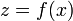

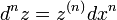
При вычислении дифференциалов высших порядков очень важно, что 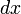есть произвольное и не зависящее от 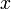, которое при дифференцировании по 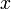следует рассматривать как постоянный множитель.

[править] Дифференциал высшего порядка функции нескольких переменных

Если функция имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так: .

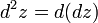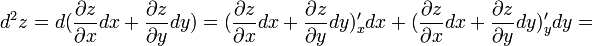
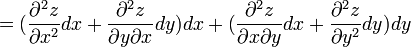
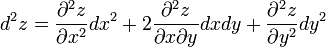
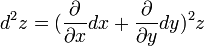
Символически общий вид дифференциала n-го порядка от функции 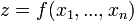выглядит следующим образом:

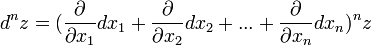
где 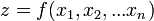, а 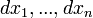произвольные приращения независимых переменных .
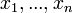Приращения 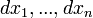рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему. Сложность выражения дифференциала возрастает с увеличением числа переменных.

23)Возрастание и убывание ф-ии. Максимум и минимум
Возрастание и убывание функции. Точки максимума и минимума функции

Рассмотрим приложение производной функции к исследованию поведения функции. По первой производной функции можно определить промежутки возрастания и убывания функции, а также определить точки экстремума функции (максимум и минимум).

Определение. Функция 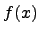называется возрастающей в точке 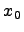, если в некоторой 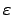-окрестности этой точки справедливо

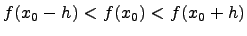
для любого .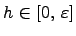

Определение. Функция 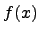называется возрастающей на отрезке 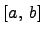, если для любых двух точек 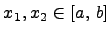справедливо неравенство

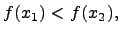
когда .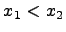

Определение. Функция 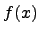называется убывающей в точке 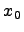, если в некоторой 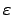-окрестности этой точки справедливо неравенство

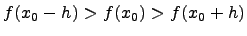
для любого .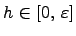

Определение. Функция 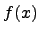называется убывающей на отрезке 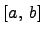, если для любых двух точек 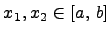справедливо неравенство

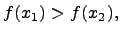
когда .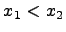

Определение. Функция 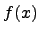имеет в точке 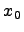максимум, если значение 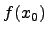является наибольшим в некоторой двустороней окрестности точки .

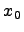Определение. Функция 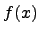имеет в точке 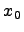минимум, если значение 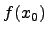является наименьшим в некоторой двусторонней окрестности точки .

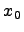Определение. Функция 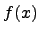имеет в точке 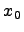экстремум, если точка 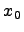является точкой максимума или минимума.

Признаки (достаточные) возрастания и убывания функции :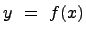

Если 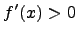на интервале 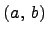, то функция 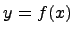возрастает на этом интервале;

Если 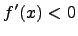на интервале 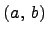, то функция 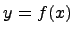убывает на этом интервале.

Необходимое условие экстремума функции.

Функция 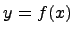может иметь экстремум только в точках, где 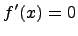или производная не существует. Точка, где 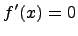или производная не существует называется критической точкой.

Заметим, что если в точке 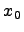выполняется, что 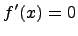, то это означает, что касательная в данной точке параллельная оси 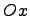. Если производная в точке 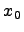не существует, то это значит либо касательная вертикальная, либо ее нет в данной точке.