Уравнение прямой, проходящей через две данные точки.

Пусть даны две точки М₁(х₁,у₁) и М₂(х₂,у₂). Запишем уравнение прямой в виде (5), где k пока неизвестный коэффициент:

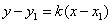
Так как точка М₂принадлежит заданной прямой, то её координаты удовлетворяют уравнению (5): 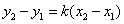. Выражая отсюда 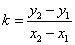и подставив его в уравнение (5) получим искомое уравнение:

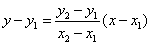
Если 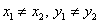это уравнение можно переписать в виде, более удобном для запоминания:

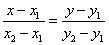(6)

Пример. Записать уравнение прямой, проходящей через точки М₁(1,2) и М₂(-2,3)

Решение. 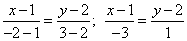. Используя свойство пропорции, и выполнив необходимые преобразования, получим общее уравнение прямой:

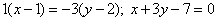
16 вопрос

Угол между двумя прямыми

Рассмотрим две прямые l₁ и l₂:

l₁: 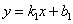, , 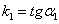и

l₂: , ,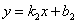

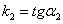φ- угол между ними ( 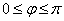). Из рис.4 видно: .

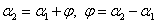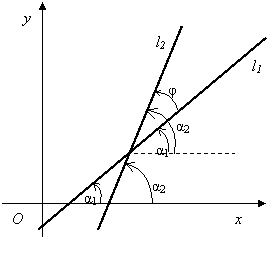Рис.4

Отсюда 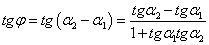, или

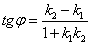(7)

С помощью формулы (7) можно определить один из углов между прямыми. Второй угол равен .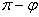

Пример. Две прямые заданы уравнениями у=2х+3 и у=-3х+2. найти угол между этими прямыми.

Решение. Из уравнений видно, что k₁=2, а k₂=-3. подставляя данные значения в формулу (7), находим

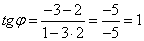. Таким образом, угол между данными прямыми равен .

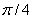Условия параллельности и перпендикулярности двух прямых

Если прямые l₁ и l₂ параллельны, то φ=0 и tgφ=0. из формулы (7) следует, что 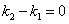, откуда k₂=k₁. Таким образом, условием параллельности двух прямых является равенство их угловых коэффициентов.

Если прямые l₁ и l₂ перпендикулярны, то φ=π/2, α₂= π/2+ α₁ . 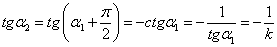. Таким образом, условие перпендикулярности двух прямых состоит в том, что их угловые коэффициенты обратны по величине и противоположны по знаку.

17 вопрос

Расстояние от точки до прямой

Теорема.Если задана точка М(х₀, у₀), то расстояние до прямой Ах + Ву + С =0 определяется как

Доказательство. Пусть точка М₁(х₁, у₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁:

(1)

Координаты x₁ и у₁ могут быть найдены как решение системы уравнений:

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М₀ перпендикулярно заданной прямой.

Если преобразовать первое уравнение системы к виду:

A(x – x₀) + B(y – y₀) + Ax₀ + By₀ + C = 0,

то, решая, получим:

Подставляя эти выражения в уравнение (1), находим:

.

Теорема доказана.

Пример. Определить угол между прямыми: y = -3x + 7; y = 2x + 1.

k₁ = -3; k₂ = 2 tgj= ; j = p/4.

Пример. Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.

Находим: k₁ = 3/5, k₂ = -5/3, k₁k₂ = -1, следовательно, прямые перпендикулярны.

Пример. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.

Находим уравнение стороны АВ: ; 4x = 6y – 6;

2x – 3y + 3 = 0;

Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b.

k= . Тогда y = . Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: откуда b = 17. Итого: .

Ответ: 3x + 2y – 34 = 0.

Расстояние от точки до прямой определяется длиной перпендикуляра, опущенного из точки на прямую.

Если прямая параллельна плоскости проекции (h | | П₁), то для того чтобы определить расстояние от точкиА до прямой h необходимо опустить перпендикуляр из точки А на горизонталь h.

Нажмите на картинку для просмотра...

На ортогональном чертеже строим отрезок A1M1 перпендикулярно h1. Далее на прямой h1 откладываем отрезок M1M0 равный А2В2. Длину перпендикуляра АM можно найти способом прямоугольного треугольника А1M1M0: |АM| = |А1M0|.

Рассмотрим более сложный пример, когда прямая занимает общее положение. Пусть необходимо определить расстояние от точки М до прямойа общего положения.

Нажмите на картинку для просмотра...

Решение задачи проводится по следующей схеме: Через заданную точку M проводится плоскость s перпендикулярная заданной прямой а. Плоскость задается двумя пересекающимися прямыми, фронталью (f) и горизонталью (h): s = h f. Находится точка пересечения (K) исходной прямойа с плоскостью s. Определяется расстояние от точки М до точки K способом прямоугольного треугольника. Длина гипотенузы прямоугольного треугольника M2K2N2 равна расстоянию от точки Mдо прямой а: |MK| = M2N2.

Задача на определение расстояния между параллельными прямыми решается аналогично предыдущей. На одной прямой берется точка, из нее опускается перпендикуляр на другую прямую. Длина перпендикуляра равна расстоянию между параллельными прямыми.

18 вопрос

Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат. В общем случае Ах² + 2Вху +Су² + 2Дх + 2Еу +F = 0,

где А, В, С, Д, Е, F – действительные числа и по крайней мере одно из чисел А²+В²+С²≠0.

Окружность

Центр окружности – это геометрическое место точек в плоскости равностоящих от точки плоскости С(а,b).

Окружность задается следующим уравнением:

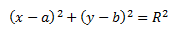
Где х,у – координаты произвольной точки окружности, R - радиус окружности.

Признак уравнения окружности

1. Отсутствует слагаемое с х,у

2. Равны Коэффициенты при х² и у²

Эллипс

Эллипсом называется геометрическое место точек в плоскости, сумма расстояний каждой из которых от двух данных точек этой плоскости называется фокусами (постоянная величина).

Каноническое уравнение эллипса:

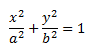
Х и у принадлежат эллипсу.

а – большая полуось эллипса

b – малая полуось эллипса

У эллипса 2 оси симметрии ОХ и ОУ. Оси симметрии эллипса – его оси, точка их пересечения – центр эллипса. Та ось на которой расположены фокусы, называется фокальной осью. Точка пересечения эллипса с осями – вершина эллипса.

Коэффициент сжатия (растяжения): ε = с/а – эксцентриситет (характеризует форму эллипса), чем он меньше, тем меньше вытянут эллипс вдоль фокальной оси.

Если центры эллипса находятся не в центре С(α, β)

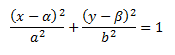
19 вопрос

Гипербола

Гиперболой называется геометрическое место точек в плоскости, абсолютная величина разности расстояний, каждое из которых от двух данных точек этой плоскости, называемых фокусами есть величина постоянная , отличная от ноля.

Каноническое уравнение гиперболы

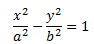
Гипербола имеет 2 оси симметрии:

а – действительная полуось симметрии

b – мнимая полуось симметрии

Ассимптоты гиперболы:

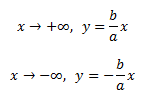
20 вопрос

Парабола

Параболой называется геометрическое место точек в плоскости, равноудаленных от данной точки F, называемой фокусом и данной прямой, называемой директрисой.

Каноническое уравнение параболы:

У²=2рх, где р – расстояние от фокуса до директрисы (параметр параболы)

Если вершина параболы С (α, β), то уравнение параболы (у-β)²=2р(х-α)

Если фокальную ось принять за ось ординат, то уравнение параболы примет вид: х²=2qу

21 вопрос