ВОПРОС№7: Каноническое уравнение эллипса
Теорема. В канонической для эллипса системе координат уравнение эллипса имеет вид:
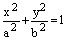 . (4)
. (4)
Доказательство. Доказательство проведем в два этапа. На первом этапе мы докажем, что координаты любой точки, лежащей на эллипсе удовлетворяют уравнению (4). На втором этапе мы докажем, что любоерешение уравнения (4) дает координаты точки, лежащей на эллипсе. Отсюда будет следовать, что уравнению (4) удовлетворяют те и только те точки координатной плоскости, которые лежат на эллипсе. Отсюда и изопределения уравнения кривой будет следовать, что уравнение (4) является уравнением эллипса.
1) Пусть точка М(х, у) является точкой эллипса, т.е. сумма ее фокальных радиусов равна 2а:
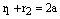 .
.
Воспользуемся формулой расстояния между двумя точками накоординатной плоскости и найдем по этой формуле фокальные радиусы данной точки М:
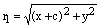 ,
, 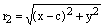 , откуда получаем:
, откуда получаем:
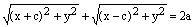 .
.
Перенесем один корень в правую часть равенства и возведем в квадрат:
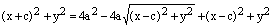 .
.
Сокращая, получаем:
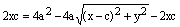 .
.
Приводим подобные, сокращаем на 4 и уединяем радикал:
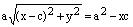 .
.
Возводим в квадрат
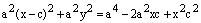 .
.
Раскрываем скобки и сокращаем на 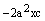 :
:
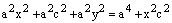 ,
,
откуда получаем:
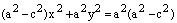 .
.
Используя равенство (2), получаем:
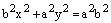 .
.
Разделив последнее равенство на 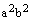 , получаем равенство (4), ч.т.д.
, получаем равенство (4), ч.т.д.
2) Пусть теперь пара чисел (х, у) удовлетворяет уравнению (4) и пусть М(х, у) – соответствующая точка на координатной плоскости Оху.
Тогда из (4) следует:
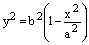 .
.
Подставляем это равенство в выражение для фокальных радиусов точки М:
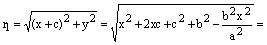
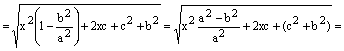
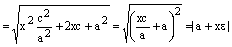 .
.
Здесь мы воспользовались равенством (2) и (3).
Таким образом, 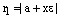 . Аналогично,
. Аналогично, 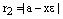 .
.
Теперь заметим, что из равенства (4) следует, что
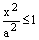 или
или 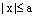 и т.к.
и т.к. 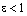 , то отсюда следует неравенство:
, то отсюда следует неравенство:
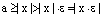 .
.
Отсюда, в свою очередь, следует, что
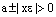 или
или 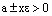 и
и
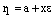 ,
, 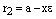 . (5)
. (5)
Из равенств (5) следует, что 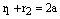 , т.е. точка М(х, у) является точкой эллипса, ч.т.д.
, т.е. точка М(х, у) является точкой эллипса, ч.т.д.
Теорема доказана.
Определение. Уравнение (4) называется каноническим уравнением эллипса.
Определение. Канонические для эллипса оси координат называются главными осями эллипса.
Определение. Начало канонической для эллипса системы координат называется центром эллипса.
ВОПРОС№8:Каноническое уравнение гиперболы.
Гиперболой называется геометрическое место точек на плоскости, разность расстояний от каждой из которых до двух данных точек F1 и F2 (фокусов) есть величина постоянная.
Вывод уравнения гиперболы. Расстояние между фокусами обозначим через 2а.Тогда
a<c.
Систему координат выберем так, чтобы ось Ох проходила через фокусы гиперболы, а ось Оу делила расстояние между фокусами пополам.
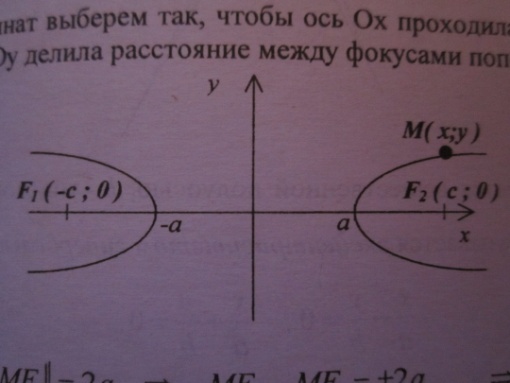
Тогда //MF2/-/MF1//=2a => MF2-MF1=+-2a =>MF2=MF1+-2a./-модуль
Каноническое уравнение: x^2/a^2-y^2/b^2=1
a-действительная полуось
в-мнимая полуось
с=корень из a^2+b^2 -фокусное расстояние
прямые
x/a-y/b=0 и x/a+y/b=0 называются ассимптотами гиперболы.
Отношение с/а=E>1 называется эксцентриситетом гиперболы.
