Описание метода Пусть исходная система выглядит следующим образом
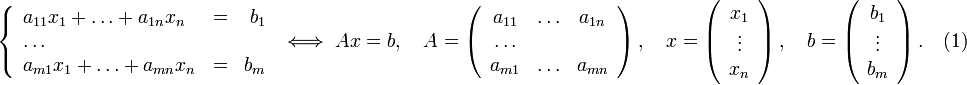
Матрица A называется основной матрицей системы, b — столбцом свободных членов.
Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):
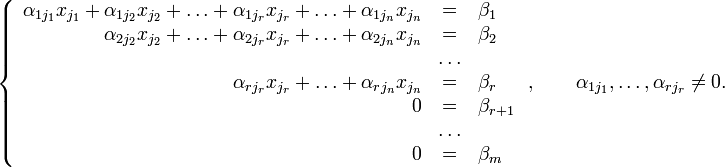
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных 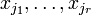 [3].
[3].
Тогда переменные 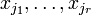 называются главными переменными. Все остальные называются свободными.
называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число 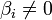 , где i > r, то рассматриваемая система несовместна.
, где i > r, то рассматриваемая система несовместна.
Пусть 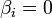 для любых i > r.
для любых i > r.
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом 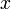 (
( 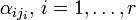 , где
, где 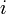 — номер строки):
— номер строки):
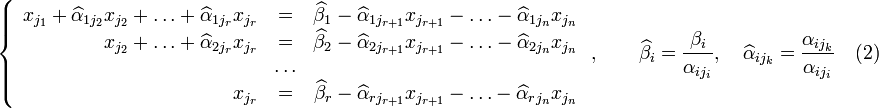 ,
,
где 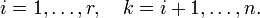
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
 | Следствия: 1: Если в совместной системе все переменные главные, то такая система является определённой. 2: Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной. |
10) Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы. Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Ранг матрицы — Размерность образа dim(im(A)) линейного оператора, которому соответствует матрица.
Обычно ранг матрицы A обозначается 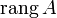 (
( 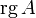 ) или
) или 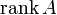 . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.
. Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.
Определение
Пусть 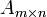 — прямоугольная матрица.
— прямоугольная матрица.
Тогда по определению рангом матрицы A является:
- ноль, если A — нулевая матрица;
- число
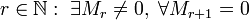 , где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к нему минор порядка (r + 1), если они существуют.
, где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к нему минор порядка (r + 1), если они существуют.
Теорема (о корректности определения рангов). Пусть все миноры матрицы 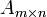 порядка k равны нулю (Mk = 0). Тогда порядка k равны нулю (Mk = 0). Тогда 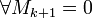 , если они существуют. , если они существуют. |
Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:
| Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. |
[правитьДоказательство (условия совместности системы)
Необходимость
Пусть система совместна. Тогда существуют числа 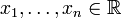 такие, что
такие, что 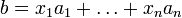 . Следовательно, столбец b является линейной комбинацией столбцов
. Следовательно, столбец b является линейной комбинацией столбцов 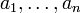 матрицы A. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что
матрицы A. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что 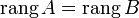 .
.
Достаточность
Пусть 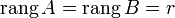 . Возьмем в матрице A какой-нибудь базисный минор. Так как
. Возьмем в матрице A какой-нибудь базисный минор. Так как 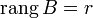 , то он же и будет базисным минором и матрицы B. Тогда согласно теореме о базисном миноре последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A.
, то он же и будет базисным минором и матрицы B. Тогда согласно теореме о базисном миноре последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A.
Следствия
- Количество главных переменных системы равно рангу системы.
- Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
11)Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества - базисных векторов.
В случае, когда базис бесконечен, понятие «линейная комбинация» требует уточнения. Это ведёт к двум основным разновидностям определения:
- Базис Га́меля, в определении которого рассматриваются только конечные линейные комбинации. Базис Гамеля применяется в основном в абстрактной алгебре (в частности в линейной алгебре).
- Базис Ша́удера, в определении которого рассматриваются и бесконечные линейные комбинации, а именно — разложение в ряды. Это определение применяется в основном в функциональном анализе, в частности для гильбертова пространства,
Ортонормированный базис. Если векторы e 1 , e 2 , e 3 попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты x 1, x 2, x 3 - прямоугольными. Базисные векторы ортонормированного базиса будем обозначать i, j, k.
Будем предполагать, что в пространстве R 3 выбрана правая система декартовых прямоугольных координат {0, i, j, k }.
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
Координаты вектора Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
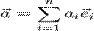
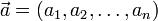
где 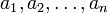 — координаты вектора.
— координаты вектора.
Свойства
- Равные векторы в единой системе координат имеют равные координаты
- Координаты коллинеарных векторов пропорциональны:
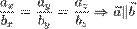
Подразумевается, что координаты вектора b не равны нулю.
- Квадрат длины вектора равен сумме квадратов его координат:
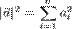
- При умножении вектора на действительное число каждая его координата умножается на это число:
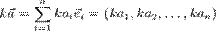
- При сложении векторов соответствующие координаты векторов складываются:
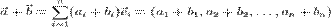
- Скалярное произведение двух векторов равно сумме произведений их соответствующих координат:
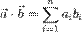
- Векторное произведение двух векторов можно вычислить с помощью определителя матрицы
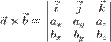
Где
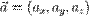
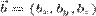
- Аналогично, смешанное произведение трех векторов можно найти через определитель
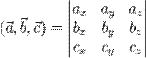
Операции над векторами
В этом разделе мы вспомним известные из школьного курса математики операции сложения векторов и умножения вектора на число, а также свойства этих операций.
Определение 10.6 Суммой векторов a и b называется такой третий вектор c, что при совмещенных началах этих трех векторов, векторы a и b служат сторонами параллелограмма, а вектор c -- его диагональю (рис. 10.2).
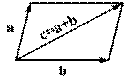
Рис.10.2.Сложение векторов
Сложение векторов в соответствии с рисунком 10.2 называется сложением по правилу параллелограмма. Однако бывает более удобным использовать для сложения правило треугольника, которое становится ясным из рисунка 1.3. Из того же рисунка видно, что результаты сложения по правилу параллелограмма и по правилу треугольника одинаковы.
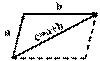
Рис.10.3.Правило треугольника
Определение 10.7 Вектор b называется противоположным вектору a, если a и b коллинеарные, имеют противоположные направления и 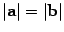 .
.
Вектор, противоположный вектору a, обозначается 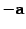 , то есть
, то есть 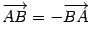 .
.
Определение 10.8 Разностью векторов a и b называется сумма 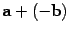 .
.
Разность обозначается 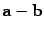 , то есть
, то есть 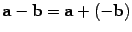 .
.
Определение 10.9 Произведением вектора a на вещественное число 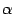 называется вектор b, определяемый условием
называется вектор b, определяемый условием
1) 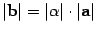
и, если 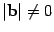 , то еще двумя условиями:
, то еще двумя условиями:
2) вектор b коллинеарен вектору a;
3) векторы b и a направлены одинаково, если 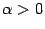 , и противоположно, если
, и противоположно, если 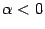 .
.
Произведение вектора a на число 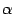 обозначается
обозначается 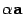 (рис 1.4).
(рис 1.4).
Коллинеарные и компланарные векторы
Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны.
Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Определение. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.
Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.
14)Определение скалярного произведения
Скалярным произведением двух ненулевых векторов а и b называетсячисло, равное произведению длин этих векторов на косинус угла междуними.
Обозначается ab,а* b(или( а, b)).Итак, по определению,
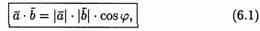
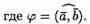
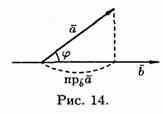
Формуле (6.1) можно придать иной вид. Так как |a| cosg=пр ba, (см. рис.14), a |b| cosg = пр ab, то получаем:

т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
