Линейные операции над матрицами.
Ответы к зачёту по математике.
1)
Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца. Определитель матрицы А обозначается как: det(A), |А| или Δ(A)
Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:
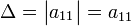
Для матрицы 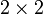 детерминант определяется как
детерминант определяется как
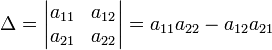
Для матрицы 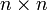 определитель задаётся рекурсивно:
определитель задаётся рекурсивно:
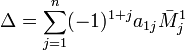 , где
, где 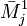 — дополнительный минор к элементу a1j. Эта формула называется разложением по строке.
— дополнительный минор к элементу a1j. Эта формула называется разложением по строке.
В частности, формула вычисления определителя матрицы 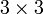 такова:
такова:
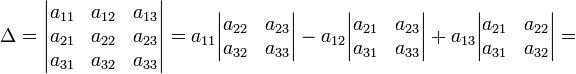
= a11a22a33 − a11a23a32 − a12a21a33 + a12a23a31 + a13a21a32 − a13a22a31
Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):
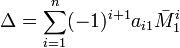
Правило Саррюса
Дописывание двух первых строк или столбцов.
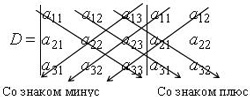
В этом случае считаем так: a11*а22*а33 + а12*а23*31+а13*а21*а32 — а13*а22*а31 — а11*а23*а32 — а12*а21*а33
2) 1.Метод разложения определителя по строке(столбцу). Для реализации данного метода необходимо проделать следующее.
- Выбрать строку или столбец данного определителя. Выберем например 1 строку.
- Взять первый элемент этой строки и записать его в правой части равенства. Это будет первый сомножитель первого слагаемого результата.
- Мысленно вычеркнуть первую строку и первый столбец данной матрицы, поскольку на пересечений первой строки и первого столбца стоит выбранный элемент матрицы. В результате получится матрица на порядок меньшая исходной. Ее определитель нужно записать в результат вычисления в качестве второго сомножителя первого слагаемого разложения определителя.
- Число минус единица надо возвести в степень, которая определяется как сумма номера строки и номера столбца. Это будет третий сомножитель первого члена разложения определителя по первой строке.
- Второй и последующие члены разложения определяются аналогично.
Таким оразом данный метод сводит задачу вычисления определителя к задаче решения определителя более низкого порядка.
3)Система 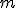 линейных алгебраических уравнений с
линейных алгебраических уравнений с 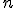 неизвестными — это система уравнений вида
неизвестными — это система уравнений вида
Здесь 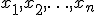 — неизвестные, которые надо определить. Коэффициенты системы
— неизвестные, которые надо определить. Коэффициенты системы 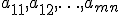 и её свободные члены
и её свободные члены 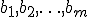 предполагаются известными. Индексы коэффициента
предполагаются известными. Индексы коэффициента 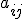 системы обозначают номера уравнения
системы обозначают номера уравнения 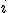 и неизвестного
и неизвестного 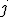 , при котором стоит этот коэффициент.
, при котором стоит этот коэффициент.
Система называется однородной, если все её свободные члены равны нулю, 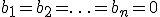 , иначе — неоднородной.
, иначе — неоднородной.
Система называется квадратной, если число 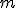 уравнений равно числу
уравнений равно числу 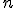 неизвестных.
неизвестных.
Решение системы уравнений — совокупность 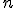 чисел
чисел 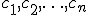 , таких что подстановка каждого
, таких что подстановка каждого 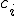 вместо
вместо 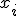 в систему обращает все её уравнения в тождества.
в систему обращает все её уравнения в тождества.
Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения. Совместная система может иметь одно или более решений.
Решения 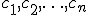 и
и 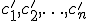 совместной системы называются различными, если нарушается хотя бы одно из равенств:
совместной системы называются различными, если нарушается хотя бы одно из равенств:
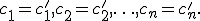
Совместная система называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.
4) Для системы n линейных уравнений с n неизвестными (над произвольным полем)
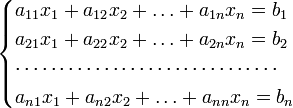
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде
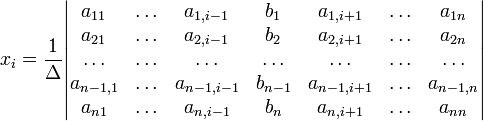
(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:
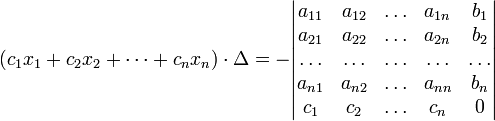
В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b1,b2,...,bn и x1,x2,...,xn, либо набор c1,c2,...,cn состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.
Определение
Пусть 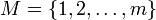 и
и 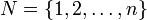 , где
, где 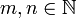 , — два конечных множества.
, — два конечных множества.
Назовём матрицей размера 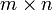 (читается m на n) с элементами из некоторого кольца или поля
(читается m на n) с элементами из некоторого кольца или поля 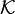 отображение вида
отображение вида
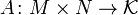 .
.
Если индекс i пробегает множество M, а j пробегает множество N, то элемент A(i,j) оказывается элементом матрицы, находящемся на пересечении i-той строки и j-ого столбца:
- i-ая строка матрицы состоит из элементов вида A(i,j), где j пробегает всё множество N;
- j-ый столбец матрицы состоит из элементов вида A(i,j), где i пробегает всё множество M.
Таким образом, матрица размера 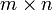 состоит в точности из
состоит в точности из
- m строк (по n элементов в каждом)
- и n столбцов (по m элементов в каждом).
В соответствии с этим
- каждую строку матрицы можно интерпретировать как вектор в n-мерном координатном пространстве
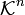 ;
; - каждый столбец матрицы — как вектор в m-мерном координатном пространстве
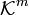 .
.
Сама матрица естественным образом интерпретируется как вектор в пространстве 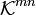 имеющим размерность mn. Это позволяет ввести покомпонентное сложение матриц и умножение матрицы на число (см. ниже); то что касается матричного умножения, то оно существенным образом опирается на прямоугольную структуру матрицы.
имеющим размерность mn. Это позволяет ввести покомпонентное сложение матриц и умножение матрицы на число (см. ниже); то что касается матричного умножения, то оно существенным образом опирается на прямоугольную структуру матрицы.
Если у матрицы количество строк m совпадает с количеством столбцов n, то такая матрица называется квадратной, а число m = n называется размером квадратной матрицы или её порядком.
Определение
Пусть 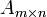 — прямоугольная матрица.
— прямоугольная матрица.
Тогда по определению рангом матрицы A является:
- ноль, если A — нулевая матрица;
- число
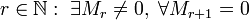 , где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к нему минор порядка (r + 1), если они существуют.
, где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к нему минор порядка (r + 1), если они существуют.
Теорема (о корректности определения рангов). Пусть все миноры матрицы 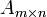 порядка k равны нулю (Mk = 0). Тогда порядка k равны нулю (Mk = 0). Тогда 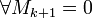 , если они существуют. , если они существуют. |
Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:
| Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. |
[правитьДоказательство (условия совместности системы)
Необходимость
Пусть система совместна. Тогда существуют числа 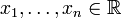 такие, что
такие, что 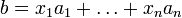 . Следовательно, столбец b является линейной комбинацией столбцов
. Следовательно, столбец b является линейной комбинацией столбцов 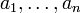 матрицы A. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что
матрицы A. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что 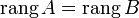 .
.
Достаточность
Пусть 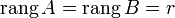 . Возьмем в матрице A какой-нибудь базисный минор. Так как
. Возьмем в матрице A какой-нибудь базисный минор. Так как 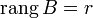 , то он же и будет базисным минором и матрицы B. Тогда согласно теореме о базисном миноре последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A.
, то он же и будет базисным минором и матрицы B. Тогда согласно теореме о базисном миноре последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A.
Следствия
- Количество главных переменных системы равно рангу системы.
- Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
11)Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества - базисных векторов.
В случае, когда базис бесконечен, понятие «линейная комбинация» требует уточнения. Это ведёт к двум основным разновидностям определения:
- Базис Га́меля, в определении которого рассматриваются только конечные линейные комбинации. Базис Гамеля применяется в основном в абстрактной алгебре (в частности в линейной алгебре).
- Базис Ша́удера, в определении которого рассматриваются и бесконечные линейные комбинации, а именно — разложение в ряды. Это определение применяется в основном в функциональном анализе, в частности для гильбертова пространства,
Ортонормированный базис. Если векторы e 1 , e 2 , e 3 попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты x 1, x 2, x 3 - прямоугольными. Базисные векторы ортонормированного базиса будем обозначать i, j, k.
Будем предполагать, что в пространстве R 3 выбрана правая система декартовых прямоугольных координат {0, i, j, k }.
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
Координаты вектора Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
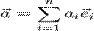
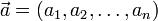
где 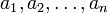 — координаты вектора.
— координаты вектора.
Свойства
- Равные векторы в единой системе координат имеют равные координаты
- Координаты коллинеарных векторов пропорциональны:
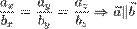
Подразумевается, что координаты вектора b не равны нулю.
- Квадрат длины вектора равен сумме квадратов его координат:
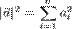
- При умножении вектора на действительное число каждая его координата умножается на это число:
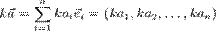
- При сложении векторов соответствующие координаты векторов складываются:
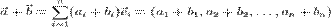
- Скалярное произведение двух векторов равно сумме произведений их соответствующих координат:
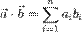
- Векторное произведение двух векторов можно вычислить с помощью определителя матрицы
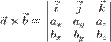
Где
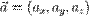
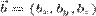
- Аналогично, смешанное произведение трех векторов можно найти через определитель
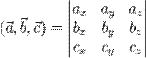
Операции над векторами
В этом разделе мы вспомним известные из школьного курса математики операции сложения векторов и умножения вектора на число, а также свойства этих операций.
Определение 10.6 Суммой векторов a и b называется такой третий вектор c, что при совмещенных началах этих трех векторов, векторы a и b служат сторонами параллелограмма, а вектор c -- его диагональю (рис. 10.2).
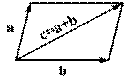
Рис.10.2.Сложение векторов
Сложение векторов в соответствии с рисунком 10.2 называется сложением по правилу параллелограмма. Однако бывает более удобным использовать для сложения правило треугольника, которое становится ясным из рисунка 1.3. Из того же рисунка видно, что результаты сложения по правилу параллелограмма и по правилу треугольника одинаковы.
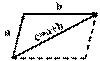
Рис.10.3.Правило треугольника
Определение 10.7 Вектор b называется противоположным вектору a, если a и b коллинеарные, имеют противоположные направления и 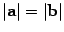 .
.
Вектор, противоположный вектору a, обозначается 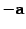 , то есть
, то есть 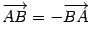 .
.
Определение 10.8 Разностью векторов a и b называется сумма 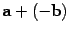 .
.
Разность обозначается 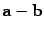 , то есть
, то есть 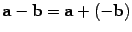 .
.
Определение 10.9 Произведением вектора a на вещественное число 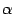 называется вектор b, определяемый условием
называется вектор b, определяемый условием
1) 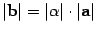
и, если 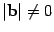 , то еще двумя условиями:
, то еще двумя условиями:
2) вектор b коллинеарен вектору a;
3) векторы b и a направлены одинаково, если 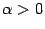 , и противоположно, если
, и противоположно, если 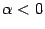 .
.
Произведение вектора a на число 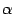 обозначается
обозначается 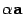 (рис 1.4).
(рис 1.4).
Коллинеарные и компланарные векторы
Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны.
Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Определение. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.
Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.
14)Определение скалярного произведения
Скалярным произведением двух ненулевых векторов а и b называетсячисло, равное произведению длин этих векторов на косинус угла междуними.
Обозначается ab,а* b(или( а, b)).Итак, по определению,
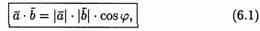
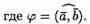
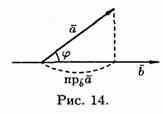
Формуле (6.1) можно придать иной вид. Так как |a| cosg=пр ba, (см. рис.14), a |b| cosg = пр ab, то получаем:

т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
Свойства
Общее уравнение прямой
Общее уравнение прямой линии на плоскости в декартовых координатах:
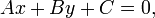
где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.
При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде :
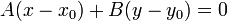
Уравнение прямой, проходящей через точку c координатами (х0;у0) с известным угловым коэффициентом:
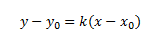
Уравнение прямой проходящей через две точки:
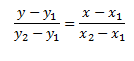
Уравнение прямой в отрезках на координатных осях:
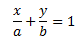
Расстояние от точки c координатами (х0;у0) до прямой Ах+Ву+С=0:
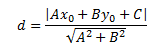
Уравнение плоскости
Рассмотрим произвольную точку 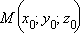 в пространстве и некоторый вектор
в пространстве и некоторый вектор 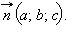 Очевидно, что геометрическим местом точек
Очевидно, что геометрическим местом точек 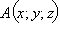 таких, что вектор
таких, что вектор 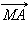 перпендикулярен вектору
перпендикулярен вектору 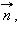 будет плоскость, проходящая через точку M перпендикулярно прямой, для которой вектор
будет плоскость, проходящая через точку M перпендикулярно прямой, для которой вектор 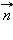 является направляющим. Нашей задачей будет установить уравнение плоскости, то есть найти соотношение, которому удовлетворяют координаты точки A.
является направляющим. Нашей задачей будет установить уравнение плоскости, то есть найти соотношение, которому удовлетворяют координаты точки A.
Запишем условие перпендикулярности векторов с использованием скалярного произведения:
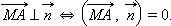 |
Запишем последнее равенство в координатах:
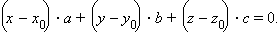 |
Поскольку все наши выкладки были равносильными, то это и есть уравнение плоскости, проходящей через заданную точку. Преобразуем его к виду
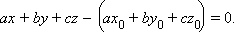 |
Обозначая 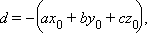 получим
получим
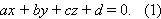 |
Это и есть так называемое общее уравнение плоскости.  Вектор
Вектор 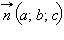 называется нормальным вектором (или просто нормалью) для плоскости, заданной общим уравнением (1).
называется нормальным вектором (или просто нормалью) для плоскости, заданной общим уравнением (1).
Нормальный вектор к плоскости перпендикулярен ей, что следует из самого вывода уравнения плоскости.
Числовые последовательности
Если каждому числу n из натурального ряда чисел: 1, 2, 3, …, n, … поставлено в соответствие вещественное число xn, то множество вещественных чисел x1, x2, …,xn, … называется числовой последовательностью или просто последовательностью.
Числа x1, x2, x3, …, xn,… будем называть элементами (или членами) последовательности, xn = f (n) – формула, по которой находится каждый член последовательности, называется общим членом последовательности. Сокращенно последовательность будем обозначать символом { xn } Примеры числовых последовательностей
- 1)
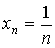
- 2)
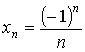
- 3) an = a1 + (n - 1)·d – арифметическая прогрессия,
- 4) xn = x1·qn - 1– геометрическая прогрессия,
- 5) xn = τ (n) – число делителей числа n,
- 6) xn = n !
Последовательность считается заданной, если указан способ получения любого ее элемента. Последовательность можно задать соотношением между двумя последовательными членами последовательности. К примеру, арифметическую прогрессию можно задать соотношением an = an-1 + d, начиная со второго члена. По самому определению, последовательность содержит бесконечное число элементов, любые два ее элемента отличаются, по крайней мере, своими номерами.
Определения
Для функций
Дифференциал функции 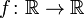 в точке
в точке 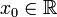 может быть определён как линейная функция
может быть определён как линейная функция
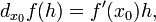
где f'(x0) обозначает производную f в точке x0.
Таким образом df есть функция двух аргументов 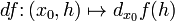 .
.
Дифференциал может быть определён напрямую, т.е., без привлечения определения производной как функция 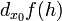 линейно зависящая от h и для которой верно следующее соотношение
линейно зависящая от h и для которой верно следующее соотношение
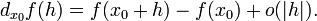
Производные высшего порядка
Пусть y = f(x) является дифференцируемой функцией. Тогда производная также представляет собой функцию от x. Если она является дифференцируемой функцией, то мы можем найти вторую производную функции f, которая обозначается в виде
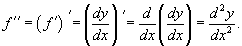
Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную функции f:
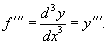
Производные более высокого порядка (если они существуют), определяются как
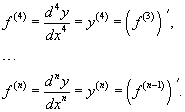
Для нахождения производных высшего порядка можно использовать следующие формулы:
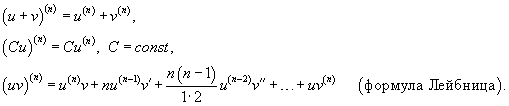
В частности, для производной второго и третьего порядка формула Лейбница принимает вид
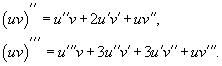
Ответы к зачёту по математике.
1)
Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца. Определитель матрицы А обозначается как: det(A), |А| или Δ(A)
Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:
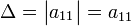
Для матрицы 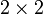 детерминант определяется как
детерминант определяется как
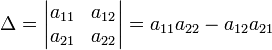
Для матрицы 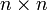 определитель задаётся рекурсивно:
определитель задаётся рекурсивно:
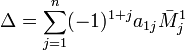 , где
, где 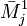 — дополнительный минор к элементу a1j. Эта формула называется разложением по строке.
— дополнительный минор к элементу a1j. Эта формула называется разложением по строке.
В частности, формула вычисления определителя матрицы 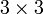 такова:
такова:
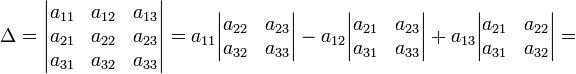
= a11a22a33 − a11a23a32 − a12a21a33 + a12a23a31 + a13a21a32 − a13a22a31
Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):
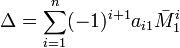
Правило Саррюса
Дописывание двух первых строк или столбцов.

В этом случае считаем так: a11*а22*а33 + а12*а23*31+а13*а21*а32 — а13*а22*а31 — а11*а23*а32 — а12*а21*а33
2) 1.Метод разложения определителя по строке(столбцу). Для реализации данного метода необходимо проделать следующее.
- Выбрать строку или столбец данного определителя. Выберем например 1 строку.
- Взять первый элемент этой строки и записать его в правой части равенства. Это будет первый сомножитель первого слагаемого результата.
- Мысленно вычеркнуть первую строку и первый столбец данной матрицы, поскольку на пересечений первой строки и первого столбца стоит выбранный элемент матрицы. В результате получится матрица на порядок меньшая исходной. Ее определитель нужно записать в результат вычисления в качестве второго сомножителя первого слагаемого разложения определителя.
- Число минус единица надо возвести в степень, которая определяется как сумма номера строки и номера столбца. Это будет третий сомножитель первого члена разложения определителя по первой строке.
- Второй и последующие члены разложения определяются аналогично.
Таким оразом данный метод сводит задачу вычисления определителя к задаче решения определителя более низкого порядка.
3)Система 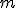 линейных алгебраических уравнений с
линейных алгебраических уравнений с 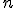 неизвестными — это система уравнений вида
неизвестными — это система уравнений вида
Здесь 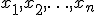 — неизвестные, которые надо определить. Коэффициенты системы
— неизвестные, которые надо определить. Коэффициенты системы 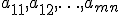 и её свободные члены
и её свободные члены 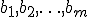 предполагаются известными. Индексы коэффициента
предполагаются известными. Индексы коэффициента 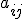 системы обозначают номера уравнения
системы обозначают номера уравнения 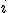 и неизвестного
и неизвестного 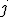 , при котором стоит этот коэффициент.
, при котором стоит этот коэффициент.
Система называется однородной, если все её свободные члены равны нулю, 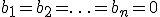 , иначе — неоднородной.
, иначе — неоднородной.
Система называется квадратной, если число 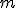 уравнений равно числу
уравнений равно числу 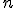 неизвестных.
неизвестных.
Решение системы уравнений — совокупность 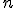 чисел
чисел 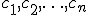 , таких что подстановка каждого
, таких что подстановка каждого 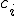 вместо
вместо 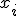 в систему обращает все её уравнения в тождества.
в систему обращает все её уравнения в тождества.
Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения. Совместная система может иметь одно или более решений.
Решения 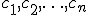 и
и 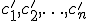 совместной системы называются различными, если нарушается хотя бы одно из равенств:
совместной системы называются различными, если нарушается хотя бы одно из равенств:
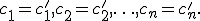
Совместная система называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.
4) Для системы n линейных уравнений с n неизвестными (над произвольным полем)
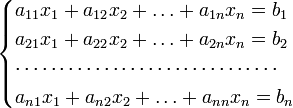
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде
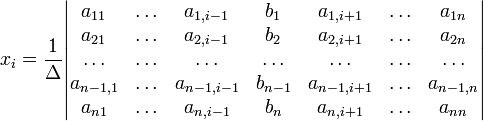
(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:
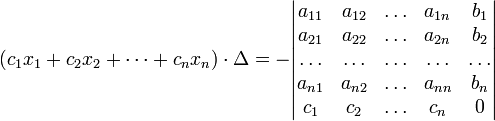
В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b1,b2,...,bn и x1,x2,...,xn, либо набор c1,c2,...,cn состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.
Определение
Пусть 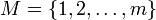 и
и 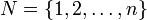 , где
, где 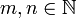 , — два конечных множества.
, — два конечных множества.
Назовём матрицей размера 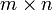 (читается m на n) с элементами из некоторого кольца или поля
(читается m на n) с элементами из некоторого кольца или поля 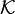 отображение вида
отображение вида
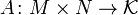 .
.
Если индекс i пробегает множество M, а j пробегает множество N, то элемент A(i,j) оказывается элементом матрицы, находящемся на пересечении i-той строки и j-ого столбца:
- i-ая строка матрицы состоит из элементов вида A(i,j), где j пробегает всё множество N;
- j-ый столбец матрицы состоит из элементов вида A(i,j), где i пробегает всё множество M.
Таким образом, матрица размера 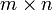 состоит в точности из
состоит в точности из
- m строк (по n элементов в каждом)
- и n столбцов (по m элементов в каждом).
В соответствии с этим
- каждую строку матрицы можно интерпретировать как вектор в n-мерном координатном пространстве
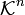 ;
; - каждый столбец матрицы — как вектор в m-мерном координатном пространстве
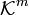 .
.
Сама матрица естественным образом интерпретируется как вектор в пространстве 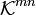 имеющим размерность mn. Это позволяет ввести покомпонентное сложение матриц и умножение матрицы на число (см. ниже); то что касается матричного умножения, то оно существенным образом опирается на прямоугольную структуру матрицы.
имеющим размерность mn. Это позволяет ввести покомпонентное сложение матриц и умножение матрицы на число (см. ниже); то что касается матричного умножения, то оно существенным образом опирается на прямоугольную структуру матрицы.
Если у матрицы количество строк m совпадает с количеством столбцов n, то такая матрица называется квадратной, а число m = n называется размером квадратной матрицы или её порядком.
Линейные операции над матрицами.
1. Сложение матриц.
Определение 3.4. Суммой матриц А и В одинаковой размерности m 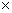 n называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах:
n называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах: 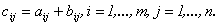
Свойства сложения:1 А + В = В + А. 2 (А + В) + С = А + (В + С) . 3. Если О – нулевая матрица, то А + О = О + А = А
ЗаЗамечание 2. Отметим еще раз, что складывать можно только матрицы одинаковой размерности.
Пример.
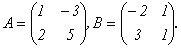
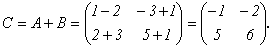
2. Умножение матрицы на число.
Определение 3.5. Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число.
Свойства умножения матрицы на число:
1. (km)A=k(mA).
2. k(A + B) = kA + kB.
3. (k + m)A = kA + mA.
Замечание 2. Назовем разностью матриц А и В матрицу С, для которой С + В =А, т.е. С = А + (-1)В.
Пример.
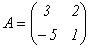 . Тогда
. Тогда 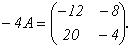
6) Умножение матриц это наиболее важная операция, которая постоянно используется в трехмерной компьютерной графике. Именно умножение матриц позволяет осуществлять преобразование векторов и комбинировать несколько преобразований в одно. Преобразования будут рассмотрены в следующем разделе.
Чтобы получить произведение матриц AB необходимо чтобы количество столбцов матрицы A было равно количеству строк матрицы B. Если условие выполняется, произведение матриц определено. Рассмотрим представленные ниже матрицы A и B, с размерностью 2 × 3 и 3 × 3 соответственно:
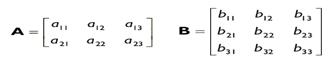
Как видите, произведение AB определено поскольку количество столбцов матрицы A равно количеству строк матрицы B. Обратите внимание, что произведение BA, получаемое в результате перестановки множителей, не определено, потому что количество столбцов матрицы B не равно количеству строк матрицы A. Это говорит о том, что в обшем случае операция умножения матриц не коммутативна (то есть AB ≠ BA). Мы говорим «в общем случае не коммутативна» по той причине, что существует ряд частных случаев в которых операция умножения матриц ведет себя как коммутативная.
После того, как мы узнали в каких случаях произведение матриц определено, можно дать определение операции умножения матриц: если A — это матрица m × n, а B — матрица n × p, то их произведением будет матрица C, размером m × p, в которой элемент cij находится как скалярное произведение i-го вектора-строки матрицы A и j-го вектора-столбца матрицы B:
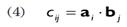
В этой формуле ai обозначает i-ый вектор-строку в матрице A, а bj — j-ый вектор-столбец матрицы B.
Давайте для примера вычислим произведение:
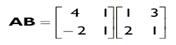
Произведение определено, поскольку количество <
