Промежутки возрастания и убывания функции. Максимум и минимум функции.
Определение возрастающей функции.
Функция y = f(x) возрастает на интервале X, если для любых 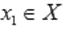 и
и 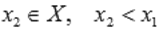 выполняется неравенство
выполняется неравенство 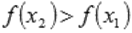 . Другими словами – большему значению аргумента соответствует большее значение функции.
. Другими словами – большему значению аргумента соответствует большее значение функции.
Определение убывающей функции.
Функция y = f(x) убывает на интервале X, если для любых 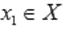 и
и 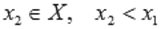 выполняется неравенство
выполняется неравенство 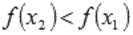 . Другими словами – большему значению аргумента соответствует меньшее значение функции.
. Другими словами – большему значению аргумента соответствует меньшее значение функции.
ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a; b), то есть при x = a и x = b, то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X.
К примеру, из свойств основных элементарных функций мы знаем, что y = sinx определена и непрерывна для всех действительных значений аргумента. Поэтому, из возрастания функции синуса на интервале 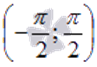 мы можем утверждать о возрастании на отрезке
мы можем утверждать о возрастании на отрезке 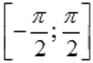 .
.
Точку 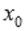 называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство
называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 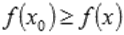 . Значение функции в точке максимума называют максимумом функции и обозначают
. Значение функции в точке максимума называют максимумом функции и обозначают 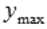 .
.
Точку 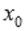 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство
называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 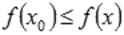 . Значение функции в точке минимума называют минимумом функции и обозначают
. Значение функции в точке минимума называют минимумом функции и обозначают 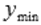 .
.
Под окрестностью точки 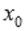 понимают интервал
понимают интервал 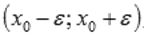 , где
, где 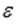 - достаточно малое положительное число.
- достаточно малое положительное число.
Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.
Достаточные признаки возрастания и убывания функции.
На основании достточных признаков находятся промежутки возрастания и убывания функции.
- если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X;
- если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X.
Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:
- найти область определения функции;
- найти производную функции
- решить неравенства f’(x)>0 и f’(x)<0 на области определения;
- к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.
Достаточные признаки экстремума функции.
Пусть функция y = f(x) дифференцируема в 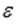 -окрестности точки
-окрестности точки 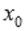 , а в самой точке
, а в самой точке 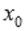 непрерывна. Тогда
непрерывна. Тогда
• если 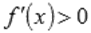 при
при 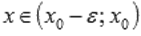 и
и 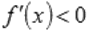 при
при 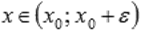 , то
, то 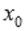 - точка максимума;
- точка максимума;
• если 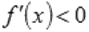 при
при 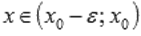 и
и 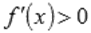 при
при 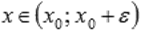 , то
, то 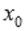 - точка минимума.
- точка минимума.
Другими словами:
• если в точке 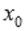 функция непрерывна и в ней производная меняет знак с плюса на минус, то
функция непрерывна и в ней производная меняет знак с плюса на минус, то 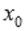 - точка максимума;
- точка максимума;
• если в точке 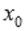 функция непрерывна и в ней производная меняет знак с минуса на плюс, то
функция непрерывна и в ней производная меняет знак с минуса на плюс, то 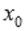 - точка минимума.
- точка минимума.
Первообразная. Неопределённый интеграл. Таблица интегралов.
Первообразная. Функция F(х) называется первообразной для функции f (х) на промежутке X, если для любого х из Х выполняется равенство F'(x)=f(x)
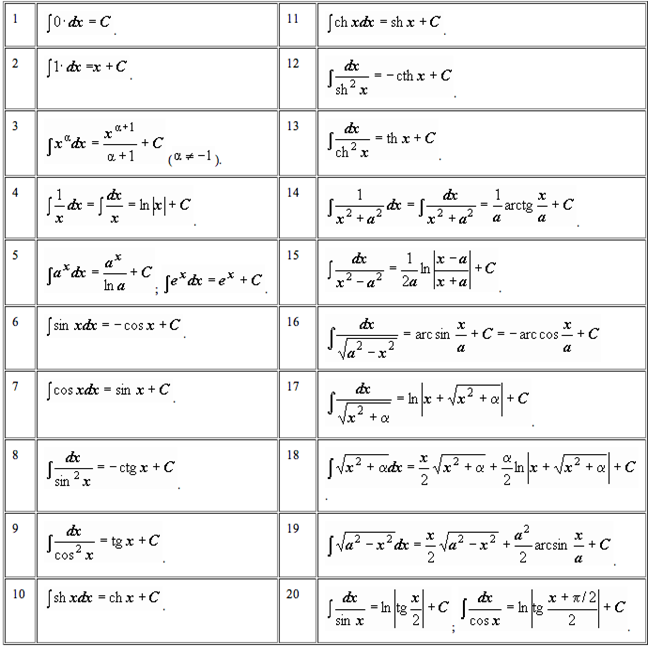
ТАБЛИЦА ПЕРВООБРАЗНЫХ

Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом 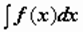 .
.
 Как следует из изложенного выше, если F(x) - некоторая первообразная функции f(x), то
Как следует из изложенного выше, если F(x) - некоторая первообразная функции f(x), то 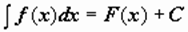 , где C - произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением.
, где C - произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением.
 Свойства неопределённого интеграла, непосредственно следующие из определения:
Свойства неопределённого интеграла, непосредственно следующие из определения:
1) 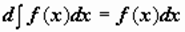 .
.
2) 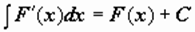 (или
(или 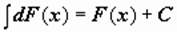 ).
).
ТАБЛИЦА ИНТЕГРАЛОВ