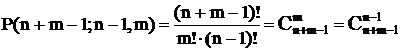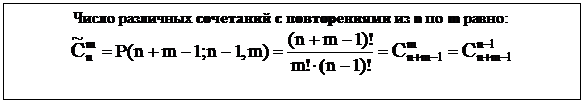Множество. Операции над множествами. Алгебра множеств.
Множество– объединение в одно целое различимых между собой элементов.
Конечное множество – множество, состоящее из конечного числа элементов.
Бесконечное множество – множество, состоящее из бесконечного числа элементов.
Пустое множество – множество, не содержащее ни одного элемента -
Универсальное –множество, содержащее все возможные элементы.
 Операции над множествами
Операции над множествами
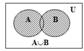
1) Объединение множеств A и B (A È B) – множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств.
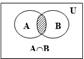 2) Пересечениемножеств A и B (AB) – множество, состоящее из всех элементов, принадлежащих каждому из этих множеств.
2) Пересечениемножеств A и B (AB) – множество, состоящее из всех элементов, принадлежащих каждому из этих множеств.
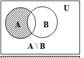 3) Разность множеств A и B (A \ B) – множество, состоящее из всех элементов множества A , не принадлежащих множеству B.
3) Разность множеств A и B (A \ B) – множество, состоящее из всех элементов множества A , не принадлежащих множеству B.
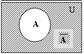 4) Дополнениемножества A в универсальном множестве U (
4) Дополнениемножества A в универсальном множестве U ( 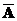 , ØA) – множество, состоящее из всех элементов универсального множества U, не принадлежащих множеству A.
, ØA) – множество, состоящее из всех элементов универсального множества U, не принадлежащих множеству A.
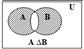 5) Симметрическая разность множеств A и B (AÅB или ADB) – множество, состоящее из всех элементов, принадлежащих в точности одному из этих множеств.A D B = (A \ B) È (B \ A) = (A È B) \ (A Ç B)
5) Симметрическая разность множеств A и B (AÅB или ADB) – множество, состоящее из всех элементов, принадлежащих в точности одному из этих множеств.A D B = (A \ B) È (B \ A) = (A È B) \ (A Ç B)
Основные законы алгебры множеств
1) коммутативные законы
А È В = В È А
А Ç В = В Ç А
А D В = В D А
2) ассоциативные законы
А È (В È С) = (А È В) È С
А Ç (В Ç С) = (А Ç В) Ç С
3) дистрибутивные законы
А È (В Ç С) = (А È В) Ç (А È С)
А Ç (В È С) = (А Ç В) È (А Ç С)
4) законы с Æ и u
А È Æ = А А Ç U = А А È  = U
= U
А Ç Æ = Æ А È U = U А Ç 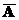 = Æ
= Æ
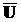 = Æ
= Æ 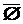 = U
= U
6) законы идемпотентности
А Ç А = А А È А = А 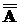 = А
= А
7) законы поглощения
А È (А Ç В) = А
А È ( 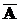 Ç В) = А È В
Ç В) = А È В
А Ç (А È В) = А
А Ç ( 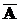 È В) = А Ç В
È В) = А Ç В
8) законы Де Моргана
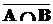 =
= 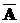 È
È 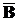
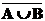 =
= 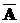 Ç
Ç 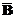
9) законы склеивания
(А Ç В) È ( 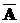 Ç В) = В
Ç В) = В
(А È В) Ç ( 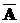 È В) = В
È В) = В
Бинарные отношения и их свойства.
Бинарное отношение на множествах X и Y – произвольное подмножество прямого произведения двух множеств r Í Х x Y = {(x,y) | xÎX, yÎY}.
Если (x,y)Îr,то (x,y) находятся в отношении rили связаны отношением r:
х r y или y = r(х)
Область определения Drбинарного отношения - множество первых элементов каждой упорядоченной пары. Dr = {x | (x,y) Î r}
Область значений Jrбинарного отношения - множество вторых элементов каждой упорядоченной пары. J r = {y | (x, y) Î r}.
Способы задания отношений
Список пар
Характеристическая функция
Графическое изображение
Матрица отношения
Свойства бинарных отношений
Пусть rзадано на множестве X, r Í Х2
1) рефлексивность:" х Î Х х r х.
2) антирефлексивность:± х Î Х х r х.
3) нерефлексивность:$ х Î Х (x, x) Ï r.
4) симметричность:" х, y Î Х х r y => y r х.
5) антисимметричность:" х, y Î Х х r y, y r х Ûx = y.
6) транзитивность:" х, y, z Î Х х r y, y r z => x r z.
Отношение порядка – антисимметрично, транзитивно.
Отношение нестрого порядка ( 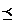 ) - рефлексивно,
) - рефлексивно,
антисимметрично,
транзитивно.
Отношениестрогого порядка ( 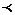 ) - антирефлексивно,
) - антирефлексивно,
антисимметрично,
транзитивно.
В отношениях полного порядка все элементы сравнимы между собой, а в отношениях частичного порядка не все элементы сравнимы между собой.
Отношение эквивалентности ( ~ )- рефлексивно,
симметрично,
транзитивно .
Класс эквивалентности для х : [ x ] = { yÎ Х | x ~ y}
Обратное отношение получается путём перестановки значений в парах исходного отношения.
Композиция отношений r иg -отношение, состоящее из пар
r○g={(x, z)| х r у, y g z }
3. Основные комбинаторные соединения (перестановки, сочетания и размещения с повторением и без повторений элементов).
Формулы пересчета для основных видов комбинаторных соединений
| Соединения | Без повторений элементов | С повторениями элементов |
| Сочетания | 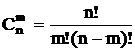 | 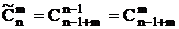 |
| Размещения | 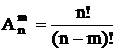 | 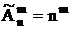 |
| Перестановки | 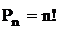 | 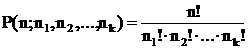 |
Соединения без повторений
Соединения – простые комбинаторные объекты, к которым относятся перестановки, сочетания и размещения.
1 Перестановка из n элементов – упорядоченная последовательность элементов n-элементного множества (кортеж).
Различные перестановки отличаются только порядком элементов в них.
Число перестановокизnразличных элементов равно: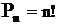
2 Размещения – упорядоченная последовательность из m элементов множества, содержащего всего n элементов.
Различные размещения отличаются составом элементов и (или) порядком их следования.
Число размещенийизnразличных элементов поmравно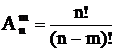
3 Сочетания из n по m – последовательность из m элементов, взятых из n-элементного множества, без учета порядка следования элементов.
Сочетание– произвольное (неупорядоченное) m-подмножество из n элементов.
Различные сочетания отличаются составом элементов, но не их порядком.
Числосочетанийизnразличных элементов поmравно: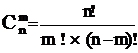 ,m ≤ n.
,m ≤ n.
Свойства сочетаний
1) 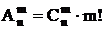 Þ
Þ 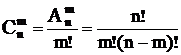 ;
;
2) 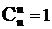 ;
; 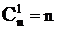 ;
; 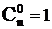 ;
; 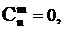 при m £ 0 и m ³n .
при m £ 0 и m ³n .
3) Симметричность числа сочетаний: 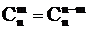 .
.
4) Правило Паскаля. Для числа сочетаний из n по m справедливо следующее рекуррентное соотношение: 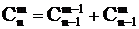 .
.
5) Бином Ньютона.
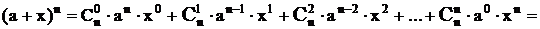
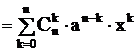
.
При a = x = 1, 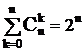 ,
, 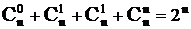 ,где
,где 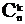 , k = 0,1… n - биномиальные коэффициенты.
, k = 0,1… n - биномиальные коэффициенты.
Соединения с повторениями
Пусть дано множество А, состоящее из n элементов, в котором n1 элементов принадлежит первому типу; n2 элементов принадлежит второму типу элементов, nk - k-тому типу. Элементы одного и того же типа неразличимы между собой.
Спецификацией множества А называется набор (n1, n2, … ,nk).
Следствие:
Если множество А, | А | = n, состоит из объектов 2 типов: m-одного типа, (n – m) –другого: 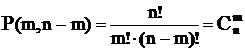
Число перестановок с повторениями n - элементного множества с
заданной спецификацией равно
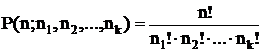 , где
, где 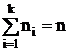 .
.
В общем случае:
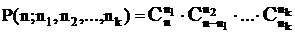 .
.
Размещения с повторениями
(m перестановки с неограниченными повторениями)
Пусть А = {a1, a2,…, an} , где a1, a2,…, an – “представители” 1-го, 2-го, … n-го типа элементов. Объектов каждого типа имеется в неограниченном количестве, элементы одного типа неразличимы между собой. Рассмотрим следующую схему выбора упорядоченной последовательности из m элементов: выбираем элемент на 1-е место, имеется n вариантов выбора. После этого элемент возвращается обратно и может быть выбран еще, т.е. на 2-е место имеется n претендентов и т.д. На m-е место также имеется n претендентов.
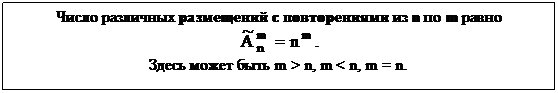 |
Сочетания с повторениями
Пусть А = {a1, a2,…, an}, где a1, a2,…, an - “представители” 1-го, 2-го, …, n-го типа элементов. Объектов каждого типа имеется в неограниченном количестве, элементы одного типа неразличимы между собой.
Сочетания с повторениями отличаются составом элементов, входящих в выбираемое множество. Порядок элементов не имеет значения. Имеет значение, сколько элементов каждого типа вошло в сочетание.