Карточка-консультация по теме

«Преобразование и вычисление значений логарифмических выражений».

Определение. Логарифмом числа b по основанию a (a>0; a≠1) называется показатель степени в которую надо возвести число a, чтобы получилось число b:

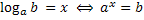
Пример 1. Вычислить без таблицы. Пример 2. правило

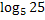= x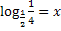

(

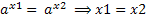
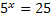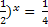
X = 2 ( = (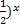

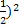
X = 2

Ответ. 2. Ответ. 2

Пример 3. Найти значение выражения.

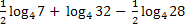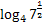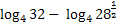= + = Применимое правило:

=

=

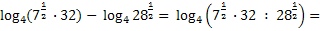
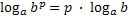
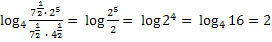
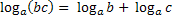
Ответ:2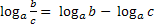

Пример 4 Найти значение выражения, применив основное логарифмическое тождество.

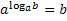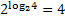
Ответ: 4

Самостоятельная работа «Логарифмы» содержит необходимое количество заданий на закрепление и систематизацию знаний и умений по теме. Карточка- консультация поможет студенту при решении самостоятельной работы.. Выполнение некоторых заданий приводит студента к расширению и углублению сферы действий уже полученных знаний. Достаточное количество вариантов обеспечивает индивидуализацию учебного процесса при активной позиции личности студента в учебной деятельности (исключается возможность механического списывания).

Задания по теме « Логарифмы»

Вариант 1.	Вариант 2.
1. При каких значениях x имеют смысл выражения:
а)	lg(x + 37) + lg(111 – 2x )	а)	lg (x + 4) + lg(2x – 2)
б)	log x (2x2 – 7x + 6)	б)	log x (3x2 + 16x + 16)
2. Решите уравнения:	2. Решите уравнения:
а)	log 2(x + 7) + log 2(x – 3) = log 211,	а)	log 3(x – 2) + log 3(x + 7) = log 310,
б)	log2 1/4x + log 1/4x – 6 = 0 .	б)	log2 5x + log 5x – 12 = 0 .
3. Решите неравенства:	3. Решите неравенства:
а)	log 39(39x + 2) ≤1 ,	а)	log 1/6(2x – 2) ≥ 0 ,
б)	log 1/8(2x – 1) + log 1/8x > 0 .	б)	log 4x + log 4(x – 3) < 1
Вариант 3.	Вариант 4.
1. При каких значениях x имеют смысл выражения:.
а)	lg(x + 3) + lg(9 – 2x)	а)	lg(x + 8) + lg(2x – 4)
б)	log x (5x2 – 17x + 14)	б)	log x (4x2 – 13x + 10)
2. Решите уравнения:	2. Решите уравнения:
а)	log 2(x – 4) + log 2(x – 5) = log 26 ,	а)	log 3(x – 3) + log 3(x + 6) = log 322 ,
б)	log2 1/9x – log 1/9x – 2 = 0 .	б)	log2 2x + log 2x – 30 = 0 .
3. Решите неравенства:	3. Решите неравенства:
а)	log 37(37x + 2) ≤1 ,	а)	log 1/5(4x – 2) ≥ 0 ,
б)	log 1/7(2x – 1) + log 1/7x > 0 .	б)	log 6x + log 6(x – 5) < 1 .
Вариант 5.	Вариант 6.
1. При каких значениях x имеют смысл выражение.
а)	lg(x + 5) + lg(15 – 2x)	а)	lg(x + 12) + lg(2x – 6)
б)	log x (4x2 – 9x – 28)	б)	log x (5x2 – 9x – 18)
2. Решите уравнения:	2. Решите уравнения:
а)	log 2(x + 12) + log 2(x–3) = log 216	а)	log 3(x – 5) + log 3(x + 8) = log 3 30
б)	log2 1/8x + 2log 1/8x – 3 = 0	б)	log2 7x – 2log 7x – 8 = 0
3. Решите неравенства:	3. Решите неравенства:
а)	log 35(35x + 2) ≤1	а)	log 1/4(6x – 2) ≥ 0
б)	log 1/3(2x – 1) + log 1/3x > 0	б)	log 8x + log 8(x – 7) < 1
Вариант 7.	Вариант 8.
1. При каких значениях x имеют смысл выражение.
а)	lg(x + 7) + lg(21 – 2x)	а)	lg(x + 16) + lg(2x – 8)
б)	log x (3x2 + 4x – 15)	б)	log x (5x2 + 11x – 36)
2. Решите уравнения:	2. Решите уравнения:
а)	log 2(x + 5) + log 2(x – 3) = log 265	а)	log 3(x – 8) + log 3(x + 2) = log 311
б)	log2 1/5x – log 1/5x – 12 = 0	б)	log2 6x – log 6x – 6 = 0
3. Решите неравенства:	3. Решите неравенства:
а)	log 33(33x + 2) ≤1	а)	log 1/5(8x – 2) ≥ 0
б)	log 1/9(2x – 1) + log 1/9x > 0	б)	lg x + lg(x – 9) < 1
Вариант 9.	Вариант 10.
1. При каких значениях x имеют смысл выражение.
а)	lg(x + 9) + lg(27 – 2x)	а)	lg(x + 20) + lg(2x – 10)
б)	log x (6x2 + 11x – 21)	б)	log x (4x2 + 23x + 33)
2. Решите уравнения:	2. Решите уравнения:
а)	log 2(x + 11) + log 2(x–4) = log 216	а)	log 3(x – 4) + log 3(x + 6) = log 324
б)	log2 1/3x – 3log 1/3x – 18 = 0	б)	log2 11x + log 11x – 2 = 0
3. Решите неравенства:	3. Решите неравенства:
а)	log 31(31x + 2) ≤1	а)	log 0.1(10x – 2) ≥0
б)	log 1/11(2x – 1) + log 1/11x > 0	б)	log 12x + log 12(x – 11) < 1

Критерии оценки задания:

Оценка «5» ставится за правильное решение 6 заданий,

Оценка «4» ставится за правильное решение 5 заданий,

Оценка «3» ставится за правильное решение 3-4 задания,

Оценка «2» ставится за правильное решение менее 3 заданий.

Самостоятельная работа №4 -8 часов

Тема: Первообразная. Неопределённый интеграл. Основные формулы интегрирования.

Методы интегрирования.

Студент должен :

Знать:

определение первообразной; определение неопределенного интеграла и его свойства; формулы интегрирования; способы вычисления неопределенного интеграла Уметь:

находить неопределенные интегралы, сводящиеся к табличным с помощью основных свойств и простейших преобразований; выделять первообразную, удовлетворяющую заданным начальным условиям;

Задание 1.Составить тест «Первообразная».

Тест должен содержать не менее 6-7 заданий и по 3-4 ответа к каждому заданию (верный только один). Включить задания двух видов:

-Вычисление первообразных различных функций.

-Вычисление первообразной, график которой проходит через точку с заданными координатами.

Форма выполнения задания: тест.

Задание 2.Подготовить рефераты на следующие темы:

-Все интересное про «Интеграл»

-О происхождении терминов и обозначений.

-Из истории интегрального исчисления.

-Обозначение интеграла: вчера и сегодня.

-Рефераты должны быть выполнены с соблюдением методических рекомендаций по написанию рефератов.

Форма выполнения задания: реферат

Задание 3:составить таблицу основных формул и свойств неопределенных интегралов.

Форма выполнения задания: таблица.

Задание 4. Используя рассмотренные свойства неопределенного интеграла. Заполните пропуски.

Карточка «Заполни пропуски»

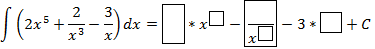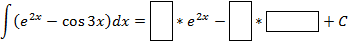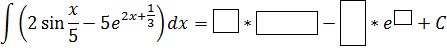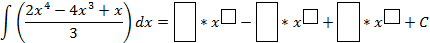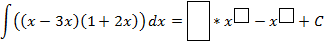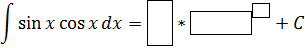Форма выполнения задания: заполнение пропусков или вычисление интегралов.

Задание 5.Вычислить неопределенные интегралы по вариантам:

1.	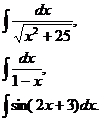2.	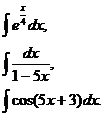3.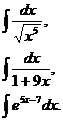
4.	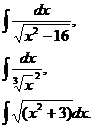5.	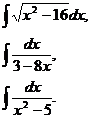6.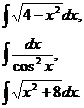

Форма выполнения задания: вычисление интегралов.

Критерии оценки задания:

Оценка «5» ставится за правильное решение 5 заданий,

Оценка «4» ставится за правильное решение 4 заданий,

Оценка «3» ставится за правильное решение 3 задания,

Оценка «2» ставится за правильное решение менее 3 заданий.

Самостоятельная работа № 5 - 8 часов.

Тема. Определенный интеграл. Формула Ньютона-Лейбница. Применение определённого интеграла для нахождения площади криволинейной трапеции.

Студент должен :

Знать:

Определенный интеграл. Формула Ньютона-Лейбница. Свойства определенного интеграла.

Уметь:

Применять определённый интеграл для нахождения площади криволинейной трапеции.

Задание 1. Ответе на вопросы:

1) Что называется первообразной?

2) Что называется неопределённым интегралом?

3) Как обозначается, читается неопределённый интеграл?

4) Что такое интегрирование?

5) Сформулировать 1 свойство неопределённого интеграла.

6) Сформулировать 2 свойство неопределённого интеграла.

7) Сформулировать 3 свойство неопределённого интеграла.

8) Дописать на доске (наверху) продолжение формулы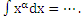

9) Дописать продолжение формулы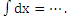

10) Дописать продолжение формулы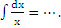

11) Дописать продолжение формулы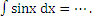

12) Дописать продолжение формулы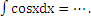

13) Дописать продолжение формулы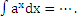

14) Как обозначается (читается) определённый интеграл

15) Основные свойства определённого интеграла

16) Дописать формулу Ньютона – Лейбница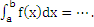

Форма выполнения задания: ответы на вопросы.

Задание 2. Составить кроссворд «Интеграл»

Форма выполнения задания: кроссворд.

Задание 3.Запишите формулы для вычисления площади заштрихованных фигур изображенных на рисунке.

Форма выполнения задания: формулы

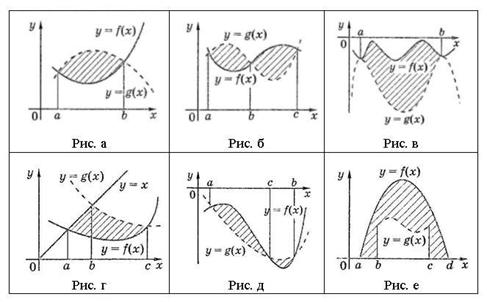
Задание 4.Вычислить площадь заштрихованной фигуры. Работа в парах.(по карточкам)

Вариант 1. вычислите площадь заштрихованной фигуры

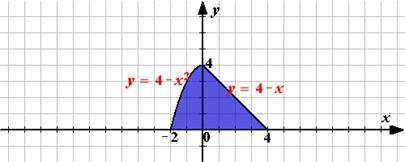
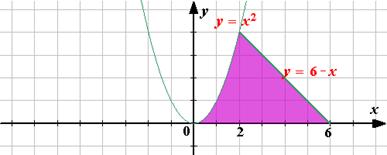
Вариант 2. Вычислите площадь заштрихованной фигуры

Вариант 3. Вычислите площадь заштрихованной фигуры

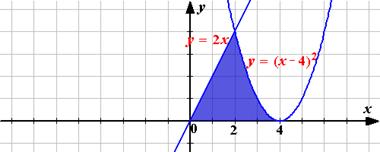
Вариант 4. Вычислите площадь заштрихованной фигуры

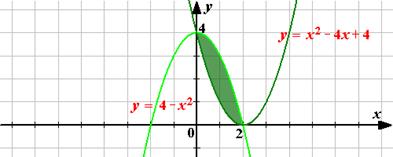
Вариант 5. Вычислите площадь заштрихованной фигуры

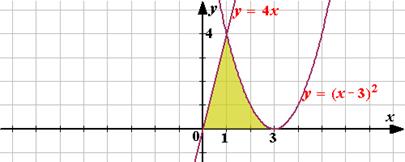
Форма выполнения задания: выполнение задания

Задание 5. Дифференцированная работа по карточкам.

Найдите площадь фигуры и определите, к какому виду относится данная площадь.

A1 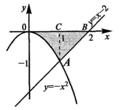Найти площадь фигуры, ограниченной линиями у=-х2, у=х -2,у=0	A2 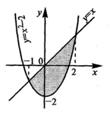Найти площадь фигуры, ограниченной линиями у= х2 -2 , у=х	A3 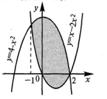  Найти площадь фигуры, ограниченной линиями y = 4 - х2, у =х2 - 2х
B1. Найти площадь фигуры, ограниченной графиками функций y=x2-2x+3, y=3x-1	B2. Найти площадь фигуры, ограниченной графиками функций y=x2, y=1+3/4x2	B3. Найти площадь фигуры, ограниченной графиками функций y=4/x2, x=1,y=x-1
C1. Найти площадь фигуры, ограниченной графиками функций y=-x2+4, y=-2/x, y=-1-x	C2. Найти площадь фигуры, ограниченной графиками функций y=x2-4, y=-2/x, y=1-x	C3. Найти площадь фигуры, ограниченной графиками функций y=log3x, y=3x, x=1,y=-3

Форма выполнения задания: выполнение самостоятельной работы.

Критерии оценки задания:

Оценка «5» ставится за правильное решение 5 заданий,

Оценка «4» ставится за правильное решение 4 заданий,

Оценка «3» ставится за правильное решение 3 задания,

Оценка «2» ставится за правильное решение менее 3 заданий.

Самостоятельная работа №6 -8 часов.

Тема. Расчетно-графическая работа по теме « Вычисление площадей геометрических фигур, ограниченных криволинейным контуром».

Студент должен :

Знать:

понятие криволинейной трапеции, способы вычисления площадей криволинейных трапеций с помощью определенного интеграла;

Уметь:

вычислять площадь криволинейной трапеции, восстанавливать закон движения по заданной скорости, скорость по ускорению, количество электричества по силе тока

Задание 1: создайте презентацию и сообщение на одну из следующих тем:

-История происхождения интегрального исчисления;

-Приложение интеграла к вычислению объёмов геометрических тел

-Приложение интеграла в физике

Презентации должны быть выполнены с соблюдением методических рекомендаций по составлению презентаций.

Форма выполнения задания: презентация.

Задание 2: подготовить сообщение на тему «История интегрального исчисления и ее роль в изучении естественно-математических наук».

Форма выполнения задания: сообщение.

Задание 3 Домашняя расчетно-графическая работа..

Самостоятельно рассмотреть пример.