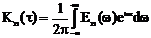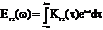Корреляционные характеристики детерминированных сигналов

Выявление соответствия между эталонным (опорным) сигналом и подобными ему сигналами, расположенными произвольно на оси времени, весьма актуально для передачи сигналов. Это два типа задач 1) обнаружение сигнала в помехах или без них, 2) измерение параметров обнаруженного сигнала (времени прихода, частоты, фазы и т.п.), которые несут информацию, но тоже могут быть поражены помехами.

а) функция автокорреляции сигнала (Баскаков, с.86)

Для количественного определения степени отличия сигнала s(t) и его сдвинутой копии s(t-τ) принято вводить функцию автокорреляции К_s (τ), равную скалярному произведению этих двух сигналов 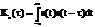Выражение (1) справедливо, если сигнал имеет локализованный во времени импульсный (финитный) характер, т.е. обладает конечной энергией, в противном случае 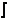- ал сходиться не будет. Свойства автокорреляционной функции: 1) при τ = 0 сходство сигнала с его несдвинутой копией достигает наибольшего значения и функция К₁₁ (0) достигает максимального значения, равного полной энергии сигнала E_s = W_s.

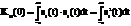2) автокорреляционная функция является четной функцией временного сдвига:

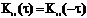Рассмотрим это свойство на примере нахождения АКФ прямоугольного видеоимпульса (рис.7.4., стр. 137 Паршин)

Рисунок

сдвиг на 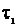в сторону запаздывания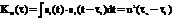

АКФ имеет размерность взаимной энергии сигналов s₁(t) и s₁(t-τ). Длительность АКФ во времени в два раза превосходит длительность прямоугольного видеоимпульса. 3) абсолютное значение АКФ при любом τ не может превышать ее значения при τ = 0 : .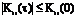

Докозательство этого неравенства вытекает непосредственно из неравенства Коши-Буняновского 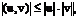т.е. взаимная энергия сигналов не может превышать произведения их норм. 4) Если функция имеет бесконечную длительность Т₁ т.е. обладает бесконечно большой энергией, то АКФ рассчитывается как среднее значение скалярного произведения сигнала его копии, следовательно, АКФ определяется в единицах мощности 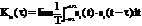Т→∞

Соответственно К₁₁(0) будет равна средней мощности сигнала .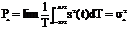

При определении АКФ периодической функции усреднение выполняется по ее периоду. 5) АКФ периодического сигнала сама является периодической функцией с тем же периодом. Докажем это на примере гармонического сигнала

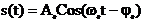
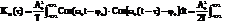
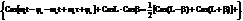
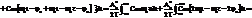
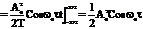Второй интеграл равен 0, т.к. площадь под Cos2ω₀t за два периода будет равна 0.При τ=0 АКФ К₁₁(0) = 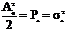определяет среднюю мощность гармонического колебания с амплитудой А₀. Из выражения (2) следует, что АКФ гармонического колебания не зависит от его начальной фазы. Это утверждение можно распространить и на другие периодические колебания.

32) Связь между энергетическим спектром сигнала и его автокорреляционной функцией.

Функция корреляции есть скалярное произведение между сигналом s и его сдвинутой на время τ копией s_τ, т.е.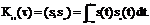

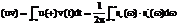
Но из обобщенной формулы Рэлея (1) - предыдущая лекция ) следует, что скалярное произведение сигналов пропорционально скалярному произведению их спектральных плотностей т.е.

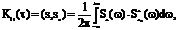но

спектральная плотность 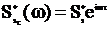и поэтому

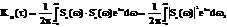(3)

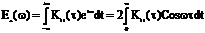(3¹)

Выражение (3¹) носит название теоремы Винера-Хинчина и имеет принципиальный характер, поскольку позволяет связывать между собой спектральные и временные характеристики не только детерминированных, но и случайных сигналов, для которых аналитическая запись формы сигнала, а значит, и его спектра, невозможна. Из (3) следует, что чем шире спектр сигнала, тем уже его автокорреляционная функция и наоборот, т.е. для сложных по форме быстроменяющихся во времени сигналов пик АКФ очень узкий. Это позволяет увеличить разрешающую способность устройств обнаружения сигналов.

Рассмотрим блок-схему устройства для обнаружения двух заранее известных сигналов s₁(t) и s₂(t) (рис. 7.5. Паршин, с.137).

Рисунок

Для определенности s₁(t) - прямоугольный видеоимпульс с заданной амплитудой и длительностью, s₂(t) - прямоугольный радиоимпульс с теми же параметрами и частотой заполнения ω₀. Считаем, что с момента t₁ до t₂ поступает видеоимпульс, а через период синхронизации Т_с радиоимпульс такой же длительности.

Пусть осуществляется когерентный прием, т.е. мы точно знаем начало и конец каждого сигнала, но не знаем - какой это сигнал s₁(t) или s₂(t). Устройство для различия двух сигналов будет двухканальным. Верхний канал следит за s₁(t), нижний за s₂(t). Это определяется спорным сигналом, подаваемым на перемножители. На выходах каналов после интегрирования в каждый момент времени будут вырабатываться напряжения, пропорциональные функциям автокорреляции или взаимной корреляции. Решение о принятом сигнале принимает устройство сравнения в моменты окончания сигналов (моменты времени t₂ и t₄). В момент времени t₂ оно примет решение о принятии сигнала s₁(t), т.к. на верхнем канале будет напряжение К₁₁ = Е_s1, а на нижнем К₂(0) = 0. В момент времени t₄ будет зафиксировано принятие радиоимпульса.

Для того, чтобы сигналы легко было различить, их АКФ должны иметь как можно более узкий главный лепесток и как можно меньший уровень побочных лепестков. Выбор сигналов для передачи должен исходить также из условия минимального значения их взаимокорреляционных функций.

В качестве сигналов с "хорошими" характеристиками можно привести набор сигналов (кодов) Баркера. У них отношение значения главного лепестка к боковым равно номеру этого сигналаМ, а ширина главного и всех побочных лепестков равны между собой и равны 2 τ_u - где τ_u - длительность элементарного сигнала (позиции), из которых составляются коды Баркера. В качестве элементарных сигналов можно использовать любые противоположные сигналы, условно обозначенные "+1" и "-1". Сигналы Баркера можно реализовать при числе позиций М = 2,3,4,5,7,11 и 13 .11 - позиционный сигнал имеет запись 1,1,1,-1,-1,-1,1, -1,-1, 1, -1. Его можно реализовать, например, как последовательность одинаковых по амплитуде и длительности разнополярных видеоимпульсов (рис. 7.6., стр. 141, Паршин. На семинарское занятие). Реализовать коды Баркера можно, например, фазоманипулированными равноимпульсами и др. способами. Не существует нечетных кодов Баркера с М>4. М7 = 1,1,1, - 1,-1, 1, -1; М5 = 1,1,1, -1,1.

33)Принцип определения взаимной функции корреляции

Обобщая формулу (1), назовем взаимной функцией корреляции двух вещественных сигналов s₁(t) и s₂(t) их скалярное произведение следующего вида: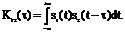

Целесообразность подобной интегральной характеристики сигналов видна из следующего примера. Пусть сигналы s₁(t) и s₂(t) в исходном состоянии ортогональны, так что 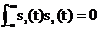.При прохождении этих сигналов через некоторые устройства возможна ситуация, когда сигнал s₁(t) будет опережать s₂(t) или, наоборот, заказывать на некоторое время τ. Взаимная функция корреляции К_{1 2} (τ) служит мерой устойчивости ортогонального состояния относительно сдвига сигнала во времени. Некоторые свойства функции взаимной корреляции:

1. Пусть даны сигналы s₁(t) и s₂(t), тогда

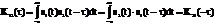
т.е. одно и тоже взаимное положение сигналов s₁(t) и s₂(t) будет достигнуто как при сдвиге s₂(t) "вправо" по оси времени, так и при сдвиге s₁(t) "влево";

2. взаимокорреляционная функция не является четной функцией аргумента τ :

;

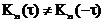3. значения ВКФ ограничены по величине, поскольку сдвиг сигнала во времени не влияет на его форму. При τ = 0 ВКФ вовсе не обязана достигать абсолютного максимума;

4. ВКФ и взаимный энергетический спектр двух сигналов связаны между собой парой преобразований Фурье: