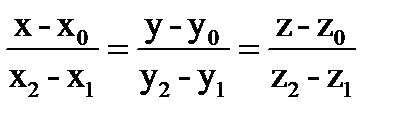Деление отрезка в данном отношении
Пусть отрезок задан точками A(x1,y1,z1) B(x2,y2,z2) и пусть l ¹ -1 – любое число.
Определение. Говорят, что точка С на отрезке АВ делит этот отрезок в отношении l если 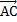 = l
= l 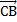
l  = 1 пополам
= 1 пополам
l=2 отношение 2:1(3 части)
l=1/2 в отно 1:2 (3 части)
Требуется наути координаты точки С.
Найти С(x,y,z)
AC = lCB ó
AC(x-x1, y-y1,z-z1)
CB(x2-x, y2-y, z2-z)
ó (x-x1, y-y1,z-z1) = l(x2-x, y2-y, z2-z) ó
x-x1 = l(x2-x)
y-y1 = l(y2-y) ó x = 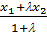
z-z1 = l(z2-z)
C( 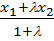 ,
, 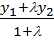 ,
, 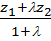 )
)
УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКУ ПЕРПЕНДИКУЛЯРНО ВЕКТОРУ.
Пусть М0(x0, y0, z0) – точка n(a,b,c) –вектор
Требуется написать ур-е плоскости a, которая проходит через точку М0 и ^n
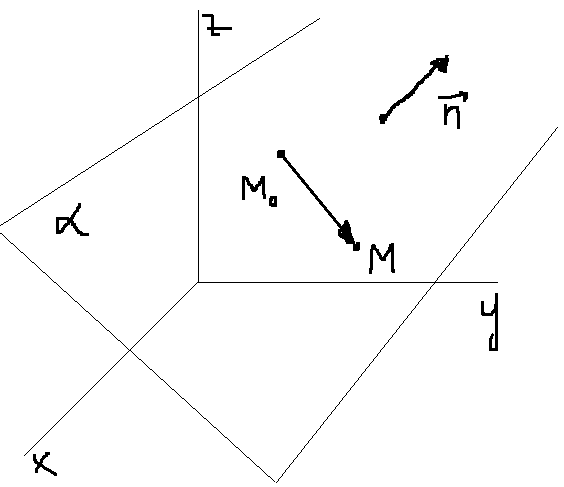
Решение.
Пусть M(x,y,z) – произвольная точка пространства. Построим вектор M0M(x-x0,y-y0,z-zo) MÎa ó M0M ^n ó M0M n = 0 ó (a,b,c)( x-x0,y-y0,z-zo) = 0 ó
a(x-x0) + b(y-y0) + c(z-z0) = 0 - уравнение плоскости, проходящей через точку перпендикулярно вектору (общее ур-е плоскости, проходящей через заданную точку) если раскрыть скобки, то получим следующее Ax+By+Cz-Ax0-By0-Cz0 = 0
Ax+By+Cz+D = 0 - общее ур-е плоскости в пространстве, где A,B,C – координаты вектора n.
УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКУ ПАРАЛЛЕЛЬНО 2-М ВЕКТОРАМ.
Пусть M0(x0,y0,z0) 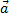 (a1,a2,a3)
(a1,a2,a3) 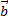 (b1,b2,b3)
(b1,b2,b3) 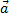
|| 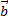
Написать ур-е плоскости a, a||a a||b M0Îa
Пусть М(x,y,z) – произвольная точка
Вектор M0M(x-x0,y-y0,z-zo)
MÎa ó M0M , 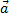 ,
, 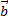 компланарны ó M0M
компланарны ó M0M 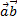 = 0 ó
= 0 ó
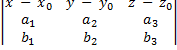 = 0
= 0
Для того, чтобы привести его к общему виду, достаточно разложить его по первой строке.
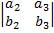 (
( 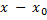 ) -
) - 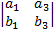 (
( 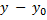 ) +
) + 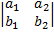 (
( 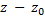 ) = 0
) = 0
УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ 3 ТОЧКИ.
Пусть даны три точки:
M0(x0,y0,z0)
M1(x1,y1,z1)
M2(x2,y2,z2)
Написать ур-е плоскости a (M0Îa, M1Îa, M2Îa)
M(x,y,z) – произвольная точка
M0M1(x1-x0,y1-y0,z1-zo) и M0M2(x2-x0,y2-y0,z2-zo) M0M(x-x0,y-y0,z-zo)
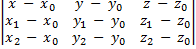 = 0
= 0
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ. УГОЛ МЕЖДУ ПЛОСКОСТЯМИ.
Дано: a: Ax + By + Cz + D = 0
M1(x1,y1,z1)
Найти: d(M1,a) – расстояние от точки до плоскости.
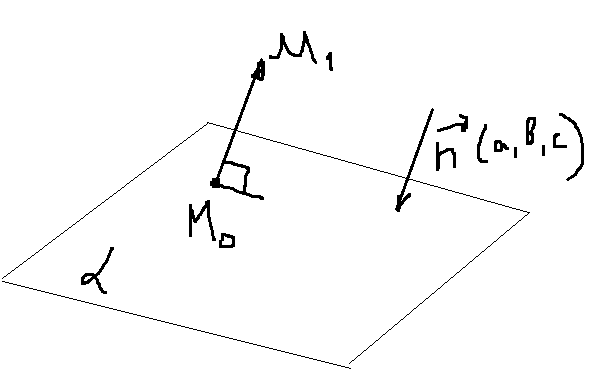
Рассмотрим M0M = |n||M0M|cos(0,p) = |n|d±1
ð d = 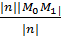
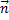 M0M1 = (A,B,C) (x1-x0,y1-y0,z1-zo) = A(x1-x0) + B(y1 – y0) + C(z1 – z0) = Ax1 + By1 + Cz1 – Ax0 –By0 –Cz0
M0M1 = (A,B,C) (x1-x0,y1-y0,z1-zo) = A(x1-x0) + B(y1 – y0) + C(z1 – z0) = Ax1 + By1 + Cz1 – Ax0 –By0 –Cz0
Т.к. М0Îa =>
=> Ax0 –By0 –Cz0 = D
=> 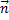 M0M1 = Ax1 + By1 + Cz1 +D
M0M1 = Ax1 + By1 + Cz1 +D
A2+B2+C2
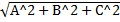
d = 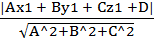
для того, чтобы найти расстояние от точки до плоскости, нужно координаты точки подставить в ур-е плоскости, взять модуль полученного числа и разделить на длину нормального вектора.
Под углом между двумя плоскостями понимают двугранный угол, образованный этими плоскостями.
N1,N2-нормальные векторы плоскости.
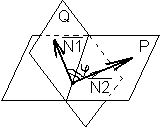 P:A1x+B1y+C1z+D1=0
P:A1x+B1y+C1z+D1=0
Q:A2x+B2y+C2z+D2=0
P^Q{A1,B1,C1}
Q^N2{A2,B2,C2}
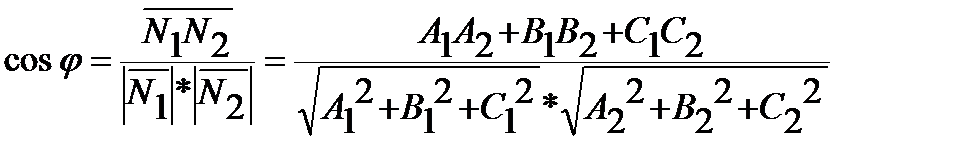
1)Пусть P^Q<=>N1^N2
A1A2+B1B2+C1C2=0 условие перпендикулярности P^Q.
2) Пусть P^Q<=> N1^N2
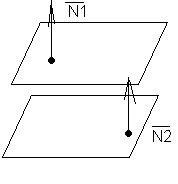
A1/A2=B1/B2=C1/C2- Условие параллельности 2х плоскостей.
A1/A2=B1/B2=C1/C2=D1/D2- Условие совпадения 2х плоскостей.
ПАРАМЕТРИЧЕСКОЕ И КАНОНИЧЕСКОЕ УРАВНЕНИЕ ПРЯМОЙ.

M0(x0,y0,z0) Î l
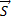 (m,n,p) – напрявляющий вектор прямой. S||l
(m,n,p) – напрявляющий вектор прямой. S||l
M(x,y,z) Î l
M0M(x-x0,y-y0,z-zo)
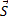 ||M0M =>
||M0M =>
M0M = 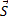 t, tÎR – параметр
t, tÎR – параметр
ìx – x0 = mt x = x0 + mt
íy – y0 = nt y = y0 + nt (1) – пар ур-е прям
î z – z0 = pt z = z0 + pt
Каноническое ур-е. Из (1) выражаем t.
t = 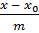
t = 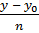
t = 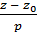
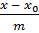 =
= 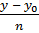 =
= 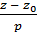 (2) - каноническое ур-е прямой
(2) - каноническое ур-е прямой
Уравнение прямой в пространстве, проходящей ч/з 2 заданные точки.
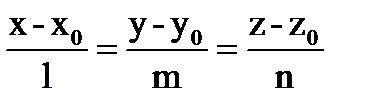
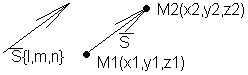
l m n
S{x2-x1,y2-y1,z2-z1}