Ортогональные системы функций и ряды Фурье

19.1. Некоторые свойства оператора Лапласа. Рассмотренные выше граничные задачи (18.1) и (18.11), а также задачи (18.41), (18,42) и ряд других можно кратко сформулировать в виде

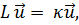(19.1)

где 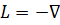² - взятый с обратным знаком оператор Лапласа, параметр к - это k² или χ ² (в. зависимости от того, является ли задача трёхмерной или двумерной), а 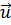– векторные или скалярные ( 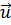= и) функции, подчинённые требуемым граничным условиям. Обычно граничные условия задаются вместе с оператором L; они определяют класс функций и, на которые может распространяться действие L, т. е. область определения оператора D_L. Разумеется, функции 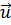, принадлежащие этому классу (кратко пишут: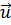 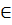D_l ), должны допускать заданные операции дифференцирования. Говорят, что запись (19.1) выражает общую формулировку задачи на собственные значения оператора L. В частности если и = 0 на S для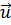 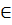D_l, получаем задачу (18.1), если и_τ = 0 и div 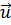= 0 на S для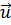 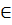D_l - задачу (18.41), и т. д.

Введём интегральную величину, имеющую своё обозначение:

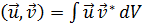(19.2)

Здесь подразумевается область V трёхмерной задачи, а в случае задачи двумерной интегрирование производится по её области S; величина 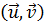называется скалярным произведениемфункций 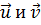, последние могут быть как векторами, так и скалярами. Заметим, что (v, и) = (и, v) *.

Оператор L, обладающий тем свойством, что для

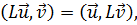(19.3)

является по определению симметрическим. Легко убедиться, что для всех поставленных в п.18 задач оператор 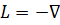² симметрический.

Действительно, в случае скалярных uиv на основании первой формулы Грина (5.13)

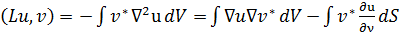(19.4)

Как для первой граничной задачи (18.1) (и = 0, v = 0 на S), так и для второй задачи (18.11) 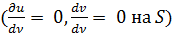поверхностный интеграл в (19.4) равен нулю. Меняя местами uи v*, мы оставляем правую часть (19.4) неизменной, а потому

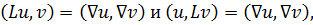(19.4а)

т. е. равенство (19.3) выполняется.

Взяв векторные 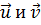, получаем:

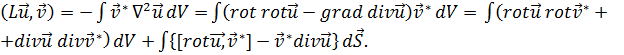(19.5)

(были использованы формулы векторного анализа (5.12), (5.10), (5.9) и (3.8)).

Если функции 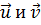подчинены граничным условиям задачи (18.41) (u_τ = 0, div 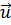= 0 и v_τ = 0, div 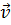= 0 на S) или граничным условиям задачи (18.42) (u_τ = 0, (rot 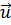)_τ = 0 и v_τ = 0, (rot 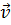)_τ = 0 на S), то поверхностные интегралы в (19.5) равны нулю, и правая часть остается неизменной при замене 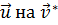и обратно. Поэтому

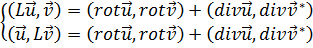, (19.5a)

и выполняется равенство (19.3).

Установленное свойство (19.3) сохраняется и для двумерных областей, т. е. при замене V на S, а граничной поверхности S объема V на контур L поверхности S. Читателю рекомендуется проверить это в качестве упражнения.

Нетрудно убедиться, что собственные значения задачи (19.1) при симметрическом операторе 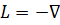² вещественны и неотрицательны. Образуя в (19.1) слева и справа скалярные произведения с 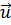, имеем:

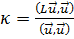(19.6)

Знаменатель 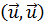положителен. В силу (19.3) 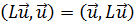, и в то же время 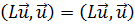*. Отсюда следует, что числитель 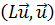- величина вещественная. Следовательно, вещественны и собственные значения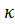

Рассматривая отдельно скалярные и векторные задачи, числитель в (19.6) преобразуем при помощи соотношений (19.4а) и (19.5а). Мы видим, что

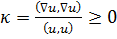(19.7)

и

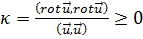(19 8)

Итак, собственные значения κ = κ_i задачи (19.1)неотрицательны и могут быть расположены в следующем порядке:

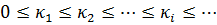(19.9)

19.2. Ортогональные системы функций. Две функции и и v называются oртогональными,если их скалярное произведение равно нулю:

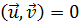. (19.10)

Пусть 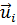(i = 1, 2, ...) - собственные функции задачи (19.1), которым соответствуют собственные значения κ; предположим, что все κ_i различны, или, как говорят, отсутствует вырождение. Взяв две любые собственные функции 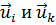, перепишем формулировку (19.1):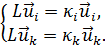

Образуя скалярные произведения ( 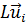, ) и ( , ) и 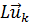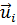принимая во внимание вещественность собственных значений, получаем:

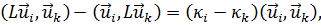
или, в силу симметричности L

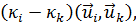= 0, (19.11)

а отсюда следует, что 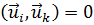,т. е собственные функции и_i ортогональны.

Задача на собственные значения (19.1) порождает, таким образом, ортогональные системы функций .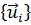

Ортогональная система 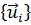всегда может быть нормирована, т. е. можно так подобрать постоянные коэффициенты в выражениях 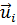, что 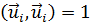для всех i. Тогда получается ортонормированная система, для которой

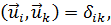(19.12)

где δ_ik= 0 при i ≠ к и δ_ik = 1 при i = k (символ Кронекера). Путём проверки нетрудно убедиться, что различные собственные функции, полученные в п.18, образуют ортогональные системы. Возьмём, например, систему функций и^тпр (18.14):

.

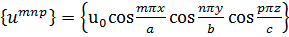Скалярное произведение двух функций и^тпр и 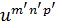имеет вид:

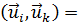
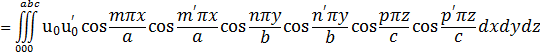
(i и k надо понимать как совокупность чисел т, п, р и т', п', р' соответственно). Поскольку

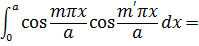
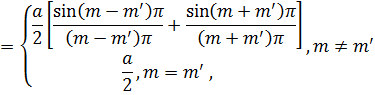
и таковы же интегралы по у и z, то, как видно, скалярное произведение действительно обращается в нуль при i ≠ k (т. е. т ≠ т', п ≠ п' и р ≠ р'). Отсюда же следует, что система 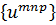будет ортонормированной, если взять

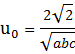
при т ≠0, п ≠0, р ≠0. Когда среди чисел т, п и р имеются нули, и₀ столько раз делится на 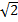, каково число нулей (один, два или три).

Предлагаю при помощи формул (16.24) и (16.26) проверить ортогональность и ввести нормировку функций и^пт (18.29). При этом следует отдельно рассматривать функции с С ≠0, D = 0 и С =0, D ≠ 0 (либо Q ≠ 0, Т = 0 и Q = 0,T ≠ 0).

19.3. Ортогональные ряды. Взяв ортонормированную систему функций 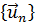и некоторую функцию 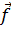, определённую в той же области, построим ряд

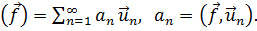(19.13)

Он называется ортогональным рядом, или рядом Фурьефункции 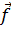, а а_п - коэффициентами Фурье.

Отличительным свойством ряда Фурье 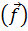является выполнение равенства

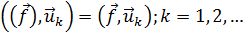(19.14)

Действительно, составляя в (19.13) скалярное произведение с , справа получаем нуль во всех членах кроме k-го, который дает а_k;равенство (19.13) превращается в выражение коэффициента Фурье а_k.

Говорят, что ряд Фурье 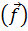сходится в среднем к 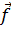, а система {и_п}полна (в этом смысле), если

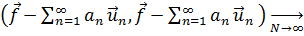0 (19.15)

Системы собственных функций оператора Лапласа обладают указанным свойством полноты при всевозможных функциях 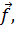которые приходится рассматривать практически (например, с разрывами второго рода).

Легко убедиться, что обычные тригонометрические ряды Фурье дают частный пример ряда (19.13).

Возьмём, например, систему собственных функций одномерного оператора Лапласа из п.7.2. После нормировки в (7.9) 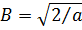, и система принимает вид:

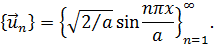
По этой системе разложим некоторую функцию f(x), определённую на отрезке 0 ≤ х ≤ а. Согласно (19.13)

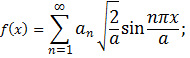
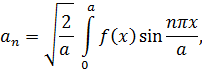
а это и есть обычный тригонометрический ряд Фурье по синусам.

В качестве второго примера рассмотрим ряд Фурье типа (12.22). В данном случае разлагается определённая на отрезке –T/2 ≤ t ≤ T/2 функция 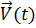, по ортонормированной системе

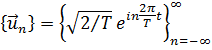
Ряд (19.13) имеет вид

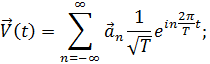
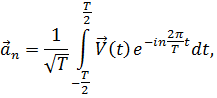
что совпадает с (12.22), (12.23). Заметим, что - это собственные функции одномерного оператора Лапласа при периодических граничных условиях и (-Т/2) = и(Т/2).

Сведения из алгебры

20.1. Векторы и матрицы. Запишем п линейных уравнений с п неизвестными:

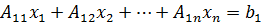
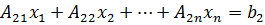(20.1)

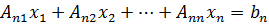
Существует ещё следующая краткая форма записи этой системы

Ах = B, (20.2)

где объект А, представляющий собой таблицу коэффициентов

A₁₁ A_{12. . . . . . . . .} A_1n

A₂₁ A_{22. . . . . . . . .} A_2n = А, (20.2а)

…………………..

A_n1 A_{n2. . . . . . . . .} A_nn

называется квадратной матрицей порядка п, а х и b - столбцы величин

x₁ b₁

x₂ b₂

_… = x и … =b (20.2б) x_n b_n

(наборы чисел), рассматриваемые как векторы.

Действительно, вектор в трёхмерном пространстве характеризуется набором трех чисел, выражающих его компоненты. Подобно этому х и b играют роль векторов в n-мерном пространстве, а систему уравнений (20.1) можно считать аналогом линейного преобразования (1.11). На векторы в n-мерном пространстве распространяются правила действий (1.2) - (1.4). А именно, суммой векторов а и b является вектор с с компонентами c_i = a_i + b_i; произведение числа т на вектор а даёт вектор с компонентами та_i; скалярное же произведение векторов с и b есть число

Формальный смысл равенства (20.2) заключен в том, что его левую часть следует рассматривать как произведение матрицы А на вектор х;с этой точки зрения, левая часть (20.1) указывает правило умножения А на х, результатом которого является вектор b с компонентами

Над матрицами также производятся алгебраические действия. Равенство

Аа + Ва = B,

где А и В - квадратные матрицы порядка п, а а и b - соответствующие векторы, можно выразить в виде

Са = B.

Здесь C - новая матрица, являющаяся суммой матриц А и В:

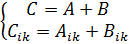(20.5)

К понятию операции умножения матрицы на матрицу приходим, имея равенства типа (20.2)

Ах = b и х = Вс.

Исключая х, запишем:

Сс = b,

где матрица С есть произведение А и В. Правило образования её элементов C_ik из A_ik и B_ik нетрудно получить, отправляясь от первоначальных форм типа (20.1). Оно имеет вид;

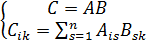(20.6)

Операция умножения матриц некоммутативна, т. е. вообще АВ ≠ ВА.

20.2. Некоторые виды матриц. Матрица называется диагональной, если все элементы A_ik при i ≠ k равны нулю, т. е.

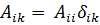(20.7)

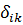( - символ Кронекера, см. § 19 п. 2); в частности, при

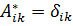(20.7а)

матрица A называется единичной и обозначается А = I; все элементы А_ii при этом равны единице, а остальные - нулю. Транспонированной по отношению к А называют матрицу А', обладающую тем свойством, что

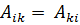. (20.8)

Матрица А' получается из А путем замены строк столбцами. Комплексно-сопряженной называется матрица А* с комплексно-сопряженными элементами:

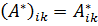. (20.9)

Введем, далее, .понятие обратной матрицы А^-1:для неё

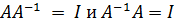. (20.10)

Матрица А может не иметь обратной и называется тогда особенной.

Поставим целью для данной матрицы А найти так называемую сопряжённую матрицу 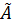, удовлетворяющую условию

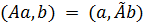, (20.11)

где а и b - произвольные векторы. На основании определения скалярного произведения векторов (20.3) должно быть:

,

т. е.

.

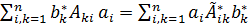При любых a и b это возможно лишь при равенстве 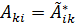для всех i и k, а следовательно,

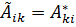(20.11а)

Мы видим, что сопряжённая матрица является транспонированной и комплексно-сопряжённой.

Если матрица Аравна сопряжённой, т. е. 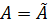и

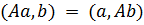, (20.12)

то ввиду (20.11а)

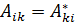. (20.12а)

Диагональные элементы такой матрицы А_и вещественны. Матрица называется эрмитовой (самосопряжённой).

Если эрмитова матрица вещественна (A* = А), и согласно (20.12а) A_ik=A_ki, т.е.

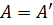, (20.13)

то говорят, что она является симметрической.

Наконец, вернемся к уравнению (20.2) и поставим вопрос, каким свойством должна обладать матрица А, чтобы выполнялось равенство

(х,х) = (b,b). (20.14)

Его можно истолковать так: при преобразовании вектора х и b последний сохраняет длину, т. е. имеет место поворот вектора в n-мерном пространстве. Выражая в (20.14) b через х,имеем:

(х, х) = (Ах, Ах).

Перепишем это с учётом (20.11) в виде:

.

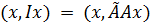Отсюда следует, что равенство (20.14) выполняется, если

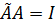, (20.15)

т. е. ввиду (20.10) сопряж`нная и обратная матрица равны. Исходная матрица A называется при этом унитарной. Если матрица A вещественна (A* = A) и унитарна, то

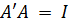. (20.16)

Такую матрицу называют ортогональной.

Заметим, что ортогональными являются матрицы преобразований, рассмотренных в § 14, составленные из направляющих косинусов для декартовой системы координат в трёхмерном пространстве. Элементы произвольной ортогональной матрицы тоже можно истолковать как направляющие косинусы (в n-мерном пространстве).

20.3. О задачах линейной алгебры. Одной из задач линейной алгебры является решение системы уравнений (20.1), т. е, согласно (20.2) определение вектора х при заданной матрице А и заданном векторе b. Если матрица А-неособенная (имеет обратную), то, умножая (20.2) слева на A^-1, сразу получаем формальное решение задачи:

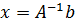. (20.17)

Можно сказать, что решение системы уравнений (20.1) сводится к обращению её матрицы А. Показывается, что

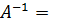
(20.18)

где Δ = DetA - определитель, соответствующий матрице А, а Δ_ik - алгебраические дополнения к элементам A_ik; эти понятия считаются известными читателю. Можно отметить, что в (20.18) фигурируют алгебраические дополнения не к тем элементам матрицы А_iк, на местах которых они находятся, а к транспонированным. Очевидно, матрица А - особенная, если Δ = 0.

Рассмотрим однородную систему уравнений, в матричной форме имеющую вид:

Аа = κа, (20.19)

где κ - некоторый параметр (число). Это формулировка задачи на собственные значения матрицы А (ср. § 19, п. 1).

Для того чтобы однородная система имела решение (отличное от нулевого) её определитель должен обращаться в нуль, т. е. в данном случае должно быть:

Det |A - κ I| = 0, (20.20)

или в подробной записи:

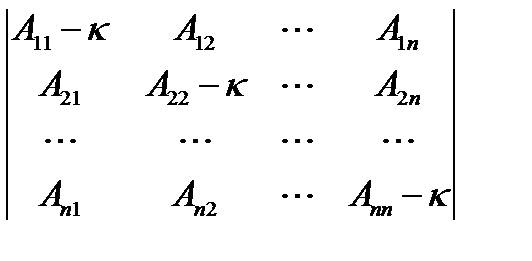= 0. (20.20а)

Уравнение (20.20) называют характеристическим (или вековым) уравнением матрицы А. Собственные значения матрицы κ = κ_i являются его корнями.

Различные способы обращения матриц и нахождения их собственных значений излагаются в курсах линейной алгебры и вычислительной математики (см., напр., [4]).

Проекционные методы

21.1. Исходные представления. Метод Галёркина. Вернемся к рядам Фурье (п.19.3), чтобы провести следующее сравнение.

Пусть в трехмерном пространстве выбрана декартова система координат и, следовательно, имеются три единичных взаимно перпендикулярных вектора: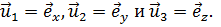

Взяв произвольный вектор 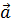, мы можем разложить его по этим ортам (рис. 21.1),что даёт:

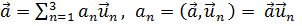(21.1)

Вектор 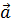теперь представлен при помощи трёх своих проекций 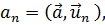являющихся скалярными произведениями 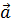на единичные базисные векторы .

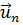Сопоставляя (21.1) и (19.13), замечаем отчётливую формальную аналогию между построенным разложением обычного вектора 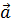и рядом Фурье функции 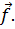Функция подобна вектору в бесконечномерном пространстве, а её ряд Фурье можно рассматривать как разложение этого вектора в базисе, образованном ортонормированной системой .

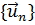Далее, пусть поставлена задача (быть может, некоторая граничная задача электродинамики) в виде

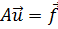, (21.2)

где A - дифференциальный оператор, заданный с надлежащими граничными условиями. Разность 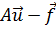равна нулю, а потому равны нулю её проекции на базис 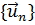, коэффициенты Фурье :

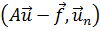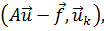k = 1, 2, …, ∞ (21.3)

В большинстве случаев замкнутые аналитические решения задач типа (21.2) недоступны. Но существуют методы, позволяющие получать приближенные решения, которые могут быть как угодно близки к рядам Фурье настоящих решений. Такие методы называются проекционными.

Проекционный метод Галёркина состоит в том, что строится представление решения 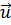в виде суммы

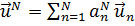(21.4)

с неопределёнными коэффициентами 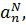и вместо (21.3) берутся N аналогичных соотношений ортогональности

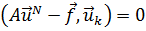; k = 1, 2, …, N. (21.5)

(разумеется, должно быть 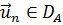, п.19.1). Легко видеть, что эти соотношения порождают систему линейных уравнений

(21.6)

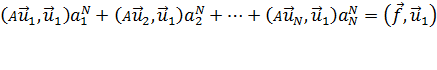
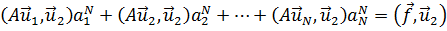
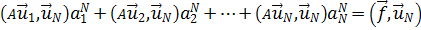
относительно коэффициентов а_п как неизвестных, т. е. в матричной форме:

Ma^N=f, (21.6а)

где в левой части фигурирует вектор, образованный этими коэффициентами 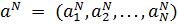и матрица М с элементами 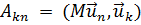,а в правой части - заданный вектор 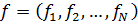с компонентами 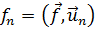(ср. п. 20.1: векторы a^N и f - это то же, что х и b в п. 20.1). Таким образом, метод Галёркина сводит граничную задачу (21.2) к системе линейных уравнений (21.6), решение которой определяет коэффициенты представления (21.4).

Возьмём теперь задачу на собственные значения вида

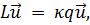(21.7)

где L - некоторый дифференциальный оператор, а q - функция координат. Подобно (21.3) имеем:

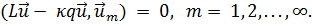(21.8)

Построив представление решения вида (21.4), подчиним его N условиям ортогональности:

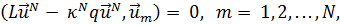(21.9)

подобно тому, как это делалось выше; индекс N при κ подчёркивает, что имеются в виду приближённые собственные значения. Из (21.9) следует однородная система линейных уравнений

Ma^N = κ^NQa^N, (21.10)

где матрицы М и Q имеют элементы M_kn = (Lu_n, u_k) и 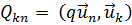соответственно.

Таким образом, первые N собственных значений задачи (21.7) приближённо определяются как корни 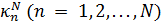характеристического уравнения

Det|M - κ^NQ| = 0(21.11)

(п. 20.3). Если, в частности q=1, то (21.11) имеет вид

Det|M - κ^NI| = 0, (21.11a)

что совпадает с (20.20). Приближёнными собственными значениями задачи (21.7) являются при этом собственные значения матрицы М.

Для широкого класса задач доказывается сходимость метода Галёркина, т. е. устанавливается тот факт, что

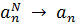при 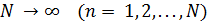, (21.12)

где а_п - коэффициенты Фурье решения .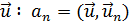

21.2. Вариационные принципы и метод Ритца. Рассматривая задачу на собственные значения (21.7), будем считать, что оператор L симметрический, функция q вещественна, а собственные значения κ_n образуют последовательность вида (19.9).

Пусть 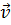- произвольная функция 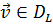.Запишем выражение

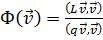(21.13)

Легко видеть, что если 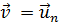- одна из собственных функций, то 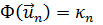есть соответствующее собственное значение.

Выражение (21.13), в котором 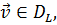может изменяться в некотором классе функций, относится к так называемым функционалам(функционал - «функция от функции»). Можно показать, что функционал 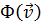имеет минимум, который равен низшему собственному значению v₁:

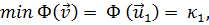(21.14)

а каждое высшее собственное значение есть также минимум Ф(u), но при некотором дополнительном условии, а именно

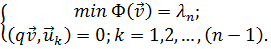(21.15)

Говорят, что функционал 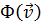(21.13) выражает вариационный принципдля задачи (21.7); вычисление собственных значений можно свести к вариационной задаченахождения 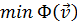(21.15) при переборе всевозможных 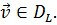Как частную форму функционала (21.13) следует рассматривать выражение (19.6), (19.7) и (19.8). Существуют также вариационные принципы совершенно иного рода, не имеющие связи с задачами на собственные значения. К ним, например, относится принцип Ферма [1].

Ограничивая класс функций, будем искать вместо 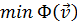величину , где 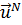есть представление (21.4) решения задачи (21.7); при этом варьируются коэффициенты 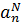.Внося (21.4) в (21.13), имеем:

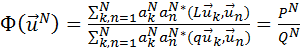(21.15)

Это функция переменных 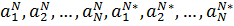(комплексно сопряженные коэффициенты - независимые переменные), и чтобы определить минимум данной функции, надо составить и обратить в нуль производные по всем переменным: условие необходимое, хотя и, вообще говоря, недостаточное. Величину примем за выражение приближённых собственных значений κ^N. Составляя равенства

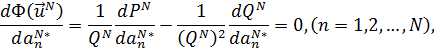
получаем:

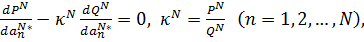(21.17)

т.е

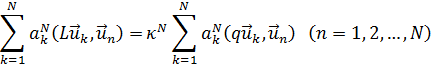
или в матричной форме с использованием обозначений из п. 1:

Ma^N = κ^NQa^N, (21.18)

что совпадает с результатом (21.10), полученным методом Галёркина. Способ, которым было найдено матричное уравнение (21.18), также относится к проекционным методам и называется методом Ритца.

Для задачи (21.2), если оператор А симметрический, тоже можно сформулировать вариационный принцип в виде функционала

(21.19)

Применяя метод Ритца, в данном случае придём к матричному уравнению (21.6а).

Уравнения (21.10), (21.6 а) и аналогичные алгебраические формы, к которым сводится граничная задача путём применения проекционных методов, называются уравнениями Галёркина-Ритца.

Список литературы

1. Бицадзе А. В. Уравнения математической физики. – М. : Наука, 1976. – 296 с.

2. Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. – М.: Наука, 1986. – 544 с.

3. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров: Пер. с англ. – М.: Наука, 1984. – 832 с.

4. Кочин И. Е. Векторное исчисление и начала тензорного исчисления – М.: Изд-во АН СССР, 1961. – 424с.

5. Лаптев Г Ф Элементы векторного исчисления. – М. Наука, 1975. – 336 с.

6. Никольский В.В. Электродинамика и распространение радиоволн / В.В. Никольский, Т.И. Никольская. – М. : Наука, 1989. – 544 с.

7. Погорелов А В. Дифференциальная геометрия – М. : Наука, 1974. – 176 с.

8. Романовский П. И. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа. – М. : Наука, 1980. – 338 с.

9. Справочник по специальным функциям с формулами, графиками и математическими таблицами. Пер. с англ. /Под ред. М. Абрамовица и И. Стиган. – М.: Наука, 1979. – 736 с.

10. Тихонов А. Н., Самарский А. А. Уравнения математической физики – М.: Наука, 1972. – 742 с.

Контрольные задания

Оглавление

Введение. 2

Глава 1. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА.. 3

1. Векторы и действия над ними. 3

1.1 Основные операции. 3

1.2. Линейное преобразование векторов. 4

1.3. Радиус-вектор. 5

2. Математическое понятие поля. Градиент. 6

2.1. Скалярное поле и градиент. 6

2.2. Градиент в декартовых координатах. 7

2.3. Векторное поле и силовые линии. 8

2.4. Потенциальные векторные поля. 8

2.5. Пример градиента. 9

3. Дивергенция. Теорема Остроградского-Гаусса. 11

3.1. Силовые линии и поток вектора. 11

3.2. Дивергенция. 12

3.3. Дивергенция в декартовых координатах. 13

3.4. Теорема Остроградского-Гаусса. 14

4. Ротор. Теорема Стокса. 16

4.1. Ротор. 16

4.2. Ротор в декартовых координатах. 16

4.3. Теорема Стокса. 17

5. Некоторые соотношения векторного анализа. 19

5.1. Оператор Гамильтона. 19

5.2. Тождества векторного анализа. 20

5.3. Теорема Грина. 22

6. Операции в криволинейных координатах. 23

6.1. Криволинейные ортогональные координаты. 23

6.2. Цилиндрические и сферические координаты. 24

6.3. Операции векторного анализа в криволинейных ортогональных координатах. 25

6.4. Операции векторного анализа в цилиндрических и сферических координатах. 27

7. О дифференциальных уравнениях с частными производными. 28

7.1 Уравнения Лапласа и Пуассона. 28

7.2. Другие уравнения. 29

7.3. Понятие линейности. 30

Глава 2. УРАВНЕНИЯ ЛАПЛАСА И ПУАССОНА.. 31

8. Дельта-функция Дирака. 31

8.1. Первоначальное понятие. 31

8.2. Обобщение и примеры.. 32

8.3. Представление дельта-функции δ (r). 34

9. Интегрирование уравнения Пуассона. 34

9.1. Функция Грина. 34

9.2. Выражение решения скалярного уравнения Пуассона. 35

9.3. Решение уравнения Пуассона для неограниченного пространства. 36

9.4. Векторное уравнение Пуассона. 37

10. Граничные задачи для уравнения Лапласа. 37

10.1. Предварительные сведения. 37

10.2. Задача Дирихле. 38

10.3. Задача Неймана. 39

11. Метод разделения переменных. 40

11.1. Сущность метода. Разделение переменных в цилиндрических координатах. 40

Глава 3. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ.. 43

12. Гармонические колебания и метод комплексных амплитуд. 43

12.1. Представление о гармонических колебаниях. 43

12.2. Метод комплексных амплитуд. 44

12.3. Средние значения. 47

12.4. Разложение по гармоническим колебаниям. 48

13. Волновые процессы и их математическое описание. 50

13.1. Плоская однородная волна. 50

13.2. Гармоническая волна. 51

13.3. Волны затухающие, неоднородные и неплоские. 53

14. Вращение декартовой системы координат. 56

14.1. Направляющие косинусы. 56

14.2. Преобразование компонент векторов и координат. 57

14.3. Углы Эйлера. 58

Глава 4. РЕШЕНИЯ ВОЛНОВЫХ УРАВНЕНИЙ.. 60

15. Интегрирование неоднородного уравнения Гельмгольца и уравнения Даламбера 60

15.1. Функция Грина для уравнения Гельмгольца. 60

15.2. Выражение решения неоднородного уравнения Гельмгольца. 62

15.3. Выражение решения уравнения Даламбера. 64

15.4. Расходящиеся и сходящиеся волны. Условие излучения. 67

16. Уравнение Бесселя и цилиндрические функции. 70

16.1. Первоначальные сведения. 70

16.2. Асимптотические представления. 72

16.3. Степенные ряды; представления функций малого аргумента. 73

16.4. Функциональные соотношения. 74

16.5. Интегральное представление функций Бесселя. 75

16.6. Разложение по функциям Бесселя. 77

17. Решение однородного уравнения Гельмгольца методом разделения переменных 80

17.1. Декартовы координаты.. 80

17.2. Цилиндрические координаты. 81

Глава 5. КРАЕВЫЕ ЗАДАЧИ ЭЛЕКТРОДИНАМИКИ.. 85

18. Граничные задачи для уравнения Гельмгольца. Собственные функции и собственные значения. 85

18.1. Постановка задач. Применение прямоугольных координат. 85

18.2. Применение цилиндрических координат. 91

18.3. Заключительные замечания. 96

19. Ортогональные системы функций и ряды Фурье. 97

19.1. Некоторые свойства оператора Лапласа. 97

19.2. Ортогональные системы функций. 99

19.3. Ортогональные ряды. 101

20. Сведения из алгебры.. 104

20.1. Векторы и матрицы.. 104

20.2. Некоторые виды матриц. 106

20.3. О задачах линейной алгебры.. 108

21. Проекционные методы.. 110

21.1. Исходные представления. 110

21.2. Вариационные принципы и метод Ритца. 113

Список литературы.. 116

Контрольные задания. 117