Глава 5. краевые задачи электродинамики

Решения задач электродинамики, как уже упоминалось, определяется внутренними граничными (краевыми) задачами. Среди уравнений, для которых ставятся такие граничные задачи, особое место занимают векторные уравнения Гельмгольца относительно комплексных амплитуд напряженностей поля.

Исследование свободных полей в ограниченных объемах порождает задачи на собственные значения (см. пример в п.7.2). Совокупности решений задач такого рода для уравнения Гельмгольца образуют системы функций, обладающих важными свойствами. С одной стороны, эти системы функций, как вы увидите в курсе электродинамики, имеют ясное физическое содержание: они описывают различные типы колебаний и волн. С другой же стороны, имея подобную систему функций, можно довольно произвольную функцию разложить в ряд, который сходен с обычным рядом Фурье. В виде ряда с неопределенными коэффициентами можно представить и заранее неизвестное решение граничной задачи, а затем - найти эти коэффициенты. Такой подход является основным средством при нахождении решений внутренних задач электродинамики. Останавливаясь на этих вопросах, мы рассмотрим некоторые свойства ортогональных систем функций, порождаемых оператором Лапласа, и соответствующие ряды, а затем - общую идею проекционных методов, имеющих большое значение при построении алгоритмов для электродинамических задач, реализуемых с помощью вычислительной техники. Попутно приводятся некоторые вспомогательные сведения (в том числе из алгебры), используемые в курсе электродинамики.

18. Граничные задачи для уравнения Гельмгольца.
Собственные функции и собственные значения

18.1. Постановка задач. Применение прямоугольных координат. В п. 17 методом разделения переменных была найдена общая форма решения уравнения Гельмгольца в декартовых координатах. Возьмем теперь объем Vс ограничивающей его поверхностью S, и поставим следующую первую граничную задачу:

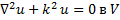
Рис. 18.1

Располагая общей формой решения (17.6), мы без труда найдём решение этой граничной задачи в случае, когда Vесть параллелепипед (рис. 18.1а). Формулировка (18.1) при этом принимает вид:

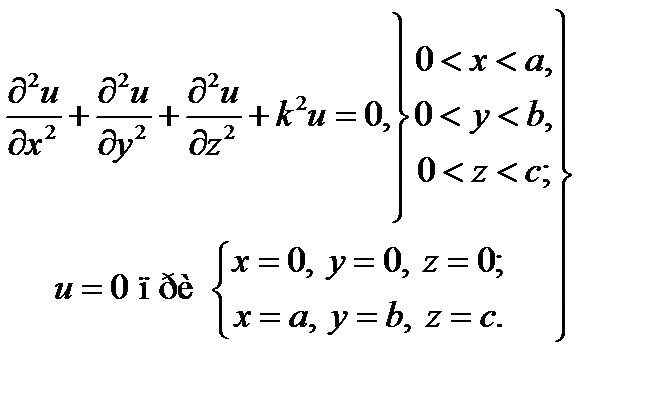(18.2)

Требуется найти функцию и(х, у, z)вида (17.6), обращающуюся в нуль на всех гранях параллелепипеда. Проще искать её в форме первой строчки (17.6):

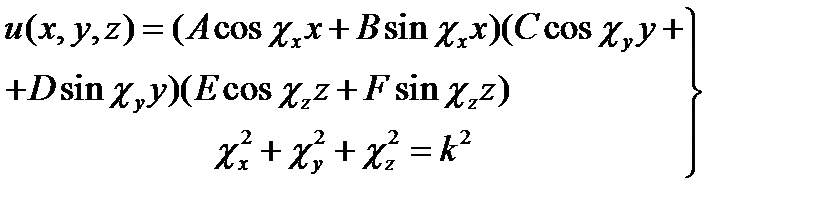(18.3)

Налагая граничное условие u(0, х, у) = 0, потребуем выполнения равенства

;

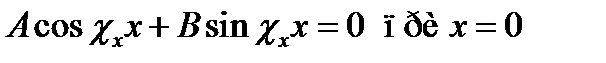(условие должно удовлетворяться при всех возможных значениях у и z).

Отсюда А = 0. Далее, требуя обращения в нуль и(х, 0, z) и и(х, у, 0), точно так же приходим к выводу, что С = 0 и Е = 0, а следовательно,

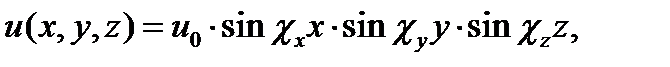, (18.4)

где и₀- постоянная, образовавшаяся как произведение неопределённых коэффициентов В, D и F.

Ввиду линейности и однородности уравнения Гельмгольца в (18.2) коэффициент и₀ так и останется неопределённым: решение и(х, у, z) допускает умножение на любую постоянную. Что же касается величин χ_х, χ_у и χ_z,то их определим, введя в рассмотрение ещё не использованные граничные условия из (18.2). Так как и(а, у, z) = 0 при всех возможных у и z, то, как видно из (18.4),

sinχ_xa = 0,

откуда следует, что аргумент синуса χ_xa равен нулю или кратен числу π: χ_ха = т π, т = 0, 1, 2, ... (отрицательные целые не дают ничего нового, изменяя лишь знак решения, который вообще говоря, произволен). Итак, найдено:

χ_х= т π/a, т = 0, 1, 2,… (18.5а)

Аналогично из граничных условий и(х, b, z) = 0 и и(х, у, с) = 0 получаем:

χ_y= n π/b, п = 0, 1,2, … (18.56)

и

χ_z= p π/c, p = 0, 1,2, … (18.5e)

При равном нулю т, п или р очевидно и(х, у, z) = 0. Но всякое сочетание трёх целых чисел т, п и р определит являющуюся решением (18.4) функцию

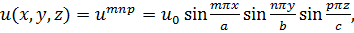(18.6)

причём согласно (18.3)

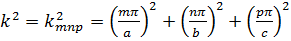(18.7)

есть то значение коэффициента k² в (18.2), при котором и^тпр является решением задачи.

Образующие бесконечную последовательность решения и^тпр называются собственными функциями задачи, а числа k_тпр - соответствующими им собственными значениями. Говорят, что граничная задача (18.2) есть задача на собственные значения.

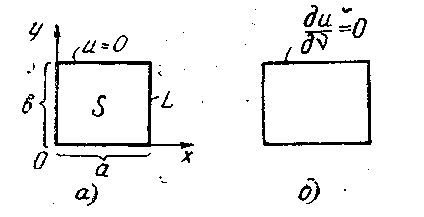
Рис. 18.2

Для двумерного уравнения Гельмгольца (17.7) аналогичная (18.2) первая граничная задача формулируется в виде:

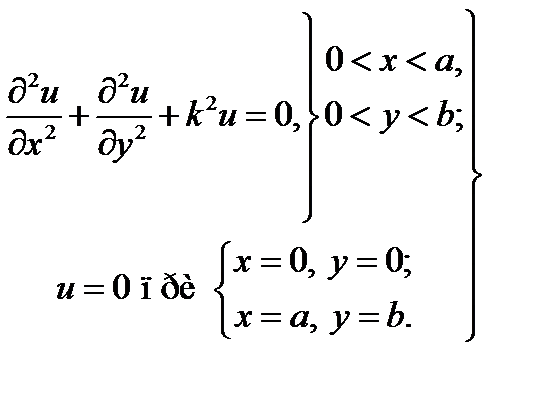_(18.8)

Отправляясь от общей формы решения (17.9), прежним способом находим, что она имеет собственные функции

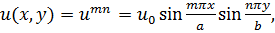(18.9)

при собственных значениях

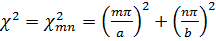. (18.10)

Решения определены в прямоугольной области S с контуром L (рис. 18.2а).

Поставим, далее, вторую граничную задачу для уравнения Гельмгольца

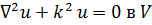
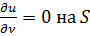(18.11)

т. е. для области V в виде параллелепипеда (рис. 18.1б):

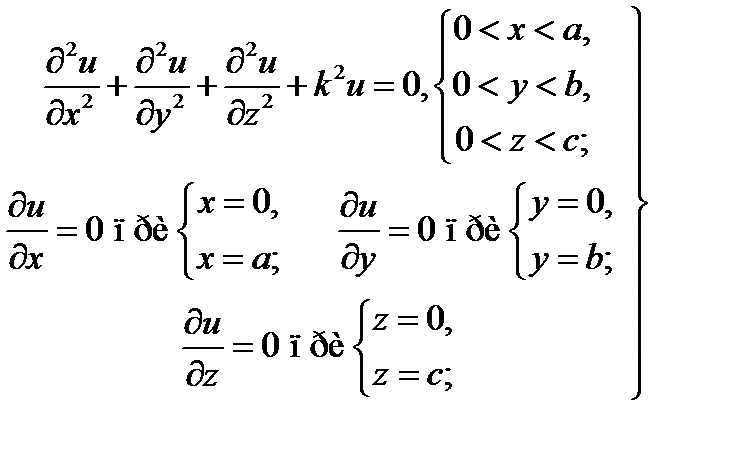(18.12)

Решение будем искать, как и ранее, исходя из его общей формы (18.3). На основании граничного условия ди/дх = 0 при х = 0 пишем:

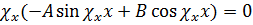при х = 0.

Отсюда B = 0. Аналогично приходим к выводу, что D = 0 и F = 0, а потому

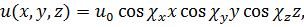(18.13)

где u₀ - постоянная, образовавшаяся как произведение неопределенных коэффициентов А, С и Е.

Граничные условия при х = а, у = b и z = с приводят к формулам, выражающим χ_х, χ_y и χ_z, которые совпадают с ранее полученными формулами (18.5а, б, в). Действительно, например, граничное условие ди/дх = 0 при х = а, как видно из (18.13), дает:

,

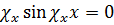a отсюда следует (18.5а).

Итак, собственные функции второй граничной задачи (18.12) имеют вид:

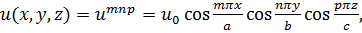(18.14)

а соответствующие им собственные значения k²_mnp по-прежнему даются формулой (18.7). Но в отличие от первой граничной задачи теперь функции и^0np, и^00p идругие с нулевыми индексами существуют (не равны тождественно нулю); при этом собственная функция и⁰⁰⁰ есть константа.

Вторая граничная задача для двумерного уравнения Гельмгольца (17.7)

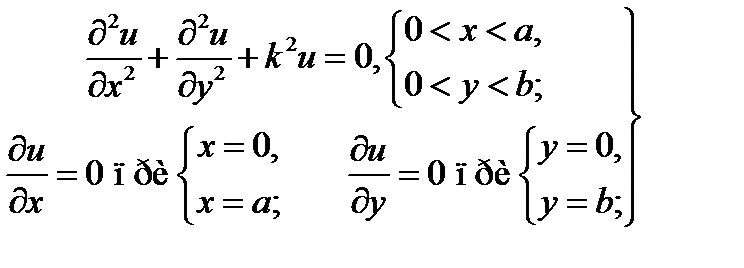(18.15)

(рис. 18,2 6) имеет, как нетрудно убедиться прежним способом, собственные функции

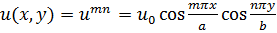(18.16)

при собственных значениях 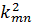вида (18.10). Собственные функции и^0п, и^т0 и u⁰⁰, не равны тождественно нулю, как в случае первой граничной задачи (18.8). Последняя из них есть константа.

В заключение отметим, что в п.7.2 была рассмотрена первая граничная задача для одномерного уравнения Гельмгольца.

18.2. Применение цилиндрических координат. Взяв уравнение Гельмгольца в цилиндрических координатах (17.10), поставим первую граничную задачу (18.1) для цилиндрической области V (рис. 18.3 а):

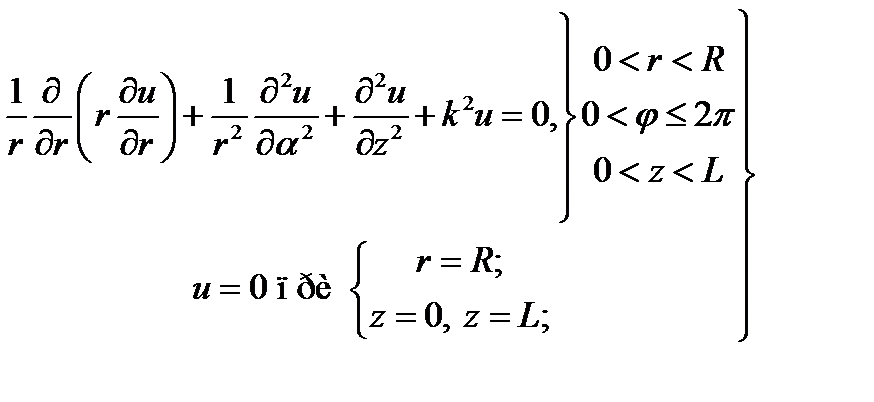(18.17)

и общую форму решения согласно (17.17) выберем в виде:

и(r, φ, z) = 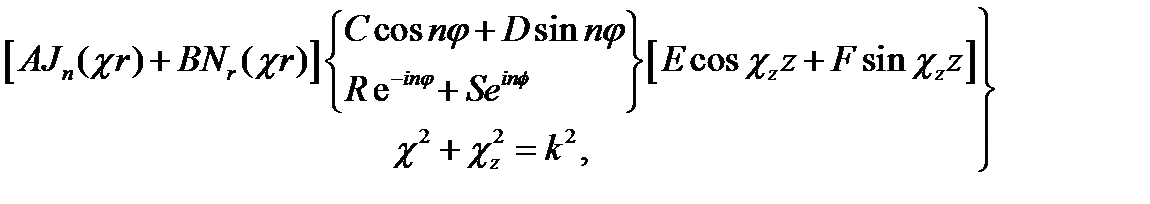(18.18)

т. е. оставляя выражение азимутальной зависимости в двух вариантах. Поскольку должно соблюдаться условие азимутальной периодичности (17.18), то п - нуль или целое: п = 0, 1, 2, ... (берём только положительные числа, так как изменение знака покрывается неопределенностью констант С, D и Q, Т).

Области V принадлежат точки оси цилиндра, а потому согласно (16.7), полагаем в (18.18) В = 0. Граничное условие на цилиндрической поверхности (r = R) требует выполнения равенства:

.

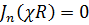Отсюда (п.16.7):

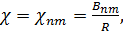(18.19)

где В_пт - корни уравнения (16.37).

Налагая граничные условия при z = 0 и z = L, как и ранее в п. 1, имеем: Е = 0, sinχ_zL= 0; последнее означает, что

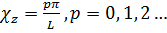(18.20)

На основании (18.18) теперь остаётся заключить, что решения граничной задачи (18.17) - это собственные функции

и(r, α, z) = и^птp =

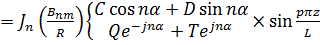(18.21)

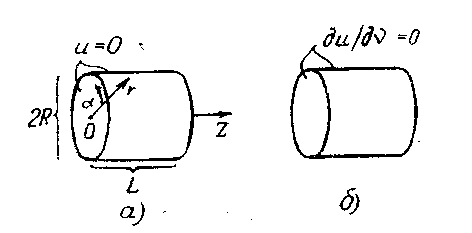
Рис. 18.3

(лишние постоянные коэффициенты опущены) при собственных значениях

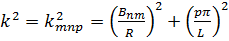(18.22)

Продолжая рассматривать цилиндрическую область, сформулируем вторую граничную задачу (18.11) для уравнения (17.10), рис. 18.3б:

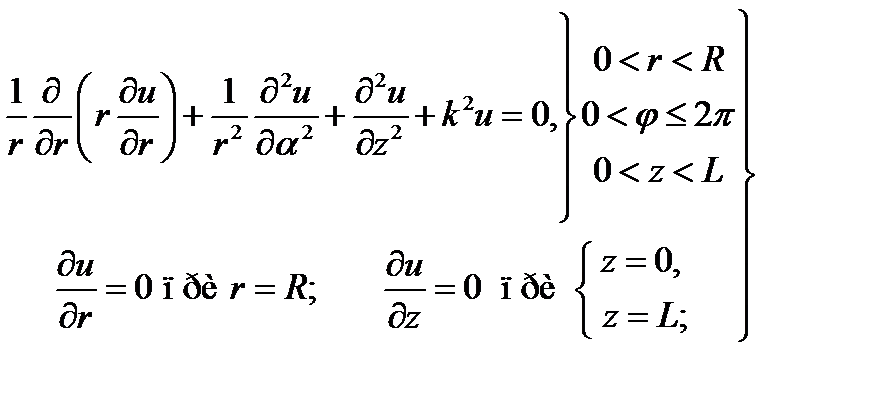(18.23)

Будем искать её решение, исходя из общей формы (18.19) и констатируя, что по-прежнему п = 0, 1, 2, ... ,и В = 0. Граничное условие на цилиндрической поверхности в данном случае влечёт равенство

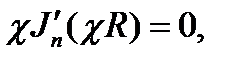
из которого следует (§ 16 п. 7):

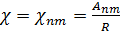(18.24)

где А_пт - корни уравнения (16.38).

Согласно граничным условиям при z = 0 и z = L (ср. п. 1), F= 0 и 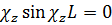, так что 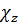определяется равенством (18.20).

Итак, вторая граничная задача (18.23) имеет собственные функции

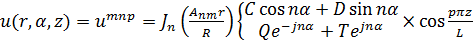(18.25)

при собственных значениях

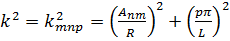(18.26)

Заметим, что в случае первой граничной задачи (18.17) собственные функций u^nm0 тождественно равны нулю; теперь же они существуют.

Перейдём к двумерным задачам. Первую граничную задачу для уравнения (17.19) поставим в разных областях S (рис 18.4а, б, в, г).

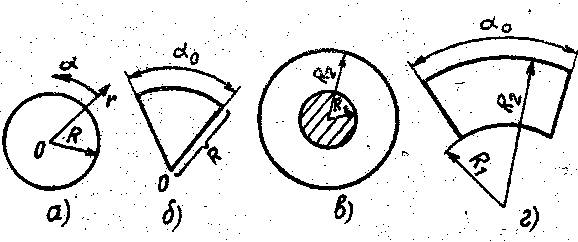
Рис 18.4

Соответственно этому,

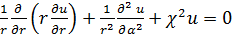: (18.27)

а) при 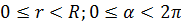(рис. 18.4а)

и = 0 при r = R; (18.27a)

б) при 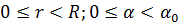(рис. 18.4б)

и = 0 при r = R; и = 0 при 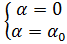(18.27б)

в) при 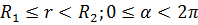(рис. 18.4 в)

и = 0 при 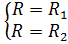; (18.27в)

г) при 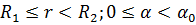(рис. 18.4г)

и = 0 при 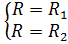; и = 0 при 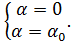(18.27г)

Исходя из общей формы решения (17.20)

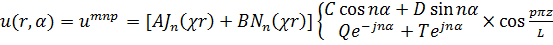,(18.28)

и повторяя предыдущие рассуждения, получим собственные функции и собственные значения задачи (18.27, 27а), рис. 18.4а:

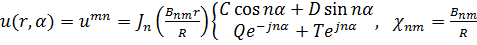(18.29)

В случае задачи (18.27, 27 6), рис. 18.4б, должно быть

.

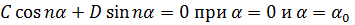Поэтому С = 0, и в отличие от предыдущего,

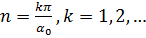(18.30)

т. е. п является целым, только если секториальная область задачи составляет целую часть полукруга. Собственные функции и собственные значения имеют вид:

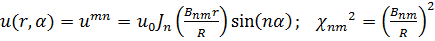. (18.31)

.

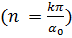В задаче (18.27, 27в), рис. 18.4в, исключены точки оси (r = 0), а потому В ≠ 0в(18.28). Налагая граничные условия (18.27в), пишем:

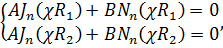
а отсюда 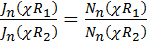(18.32)

Это не что иное как трансцендентное уравнение относительно χ = χ _пт Кроме того из записанных соотношений следует, что

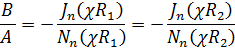
Поэтому собственные функции задачи имеют вид

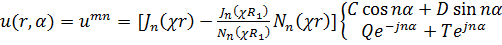, (18.33)

а собственные значения χ² = χ_пт² - это квадраты корней уравнения (18.32), входящих также в (18.33).

Далее, вы можете убедиться самостоятельно, что собственные функции задачи (18.27, 27г) имеют вид

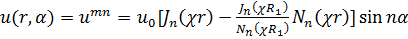, (18.34)

где n = kπ/α₀ (k = 1, 2, …), а χ = χ_пт - корни уравнения (18.33), в котором подразумевается то же n.

Вторая граничная задача для уравнения (18.27) формулируется со следующими условиями:

а) при 0 ≤ r < R; 0 ≤ α < 2π (рис. 18.4а)

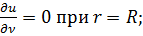(18.35)

б) при 0 ≤ r < R; 0 ≤ α < α₀ (рис. 18.4б)

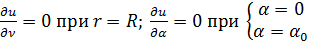(18.35б)

в) при R₁ < r < R₂;0 ≤ α < 2π (рис, 18.4в)

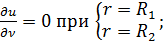(18.35в)

г) при R₁ < r < R₂;0 ≤ α < α₀ (рис. 18.4г)

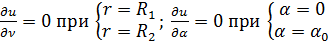(18.35г)

Опуская промежуточные выкладки, смысл которых ясен из предыдущего, выпишем лишь окончательные результаты для поставленных задач.

Собственные функции и собственные значения задачи (18.27,35а), рис. 18.4а, имеют вид:

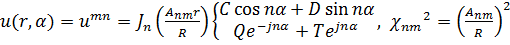(18.36)

Для задачи (18.27,35 б), рис. 38.4б

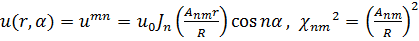(18.37)

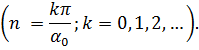
В случае (18.27,35в), рис. 18.4в

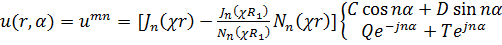, (18.38)

причем χ = χ_пт - корни уравнения

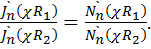(18.39)

Наконец, для задачи (18.27.35г), рис. 18.4г,

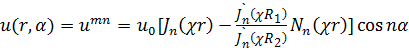, (18.40)

где n = kπ/α₀ (k =0, 1, 2, …), а χ = χ_пт - корни уравнения (18.39), с тем же n.

18.3. Заключительные замечания. Мы рассмотрели ряд задач на собственные значения для уравнения Гельмгольца. Прямоугольным и цилиндрическим координатам было отдано предпочтение потому, что описываемые в них области представляют наибольший интерес для дальнейшего; полученные результаты пригодятся, например, при изучении волноводов. Читатель может, воспользовавшись данными из § 17 п. 3, в качестве упражнения поставить и решить граничные задачи (18.1) и (18.11) также для областей, ограниченных сферическими поверхностями.

Предметом нашего внимания было скалярное уравнение Гельмгольца. Что касается векторного уравнения, то ограничимся пока лишь постановкой двух важных для электродинамики граничных задач, также являющихся задачами на собственные значения:

Первая граничная задача

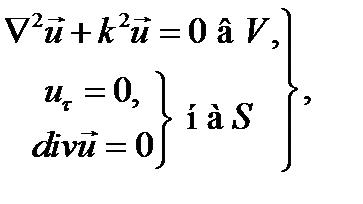(18.41)

Вторая граничная задача

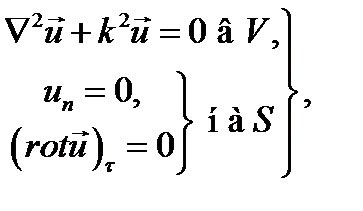(18-42)