Некоторые соотношения векторного анализа
5.1. Оператор Гамильтона. В векторном анализе широко используется так называемый оператор Гамильтона «набла»
 (5.2)
(5.2)
Это символическое обозначение дифференциальной операции, которую можно произвести как над скалярной, так и над векторной функцией. В первом случае имеем:

т. е.
 (5.3)
(5.3)
Что касается действия  на вектор, то здесь существенна векторная структура самого оператора, позволяющая понимать это действие двояко. Во-первых, очевидно,
на вектор, то здесь существенна векторная структура самого оператора, позволяющая понимать это действие двояко. Во-первых, очевидно,  можно строить по формальному правилу составления скалярного произведения двух векторов (1.4), принимая операторы дифференцирования д/дх, д/ду и д/дz за компоненты вектора. Это дает:
можно строить по формальному правилу составления скалярного произведения двух векторов (1.4), принимая операторы дифференцирования д/дх, д/ду и д/дz за компоненты вектора. Это дает:

Как видно,
 . (5.4)
. (5.4)
Но можно рассматривать и «векторное произведение» оператора  на вектор
на вектор 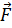 :
:

что даёт ротор вектора:
 . (5.5)
. (5.5)
Оператор Гамильтона является, таким образом, удобным средством представления операций векторного анализа. При выполнении различных действий его следует понимать как вектороподобный комплекс обычных дифференциальных операторов д/дх, д/ду и д/дz. Однако, обращаясь с  формально как с вектором, надо помнить, что не имеет смысла дописывание этого оператора справа (например,
формально как с вектором, надо помнить, что не имеет смысла дописывание этого оператора справа (например,  или
или  ), поскольку бессмысленны выражения типа
), поскольку бессмысленны выражения типа  в отличие от
в отличие от  .
.
Пользуясь формулами (3.7) и (2.5), нетрудно образовать дивергенцию градиента некоторой скалярной функции:
 (5.6)
(5.6)
Запишем это с использованием оператора Гамильтона:
 (5.6а)
(5.6а)
Оператор  (его обозначают также Δ) называется оператором Лапласа. Это один из важнейших операторов математической физики. Он применяется и к векторным функциям, при этом
(его обозначают также Δ) называется оператором Лапласа. Это один из важнейших операторов математической физики. Он применяется и к векторным функциям, при этом
 . (5.7)
. (5.7)
5.2. Тождества векторного анализа. В § 4 п. 3 были получены два важных тождества векторного анализа (4.4) и (4.5), т. е. равенства, справедливые для любых функций, к которым их применение осмысленно (в данном случае требуется существование частных производных второго порядка) и компонент 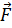 . Запишем ещё некоторые тождества, часто применяемые в теории электромагнетизма.
. Запишем ещё некоторые тождества, часто применяемые в теории электромагнетизма.
Следующие четыре тождества векторного анализа имеют значение правил дифференцирования произведения функций:
 , (5.8)
, (5.8)
 , (5.9)
, (5.9)
 (5.10)
(5.10)
 . (5.11)
. (5.11)
Вывод их весьма прост с использованием векторного дифференциального оператора «набла». При этом необходимо использовать обычные правила дифференцирования произведения. Например,

Здесь индексы операторов «набла» условно показывают, на который из двух сомножителей они действуют. В последующем эти индексы опущены за ненадобностью.
Ещё одно часто используемое тождество имеет вид:
 (5.12)
(5.12)
Его можно получить, в частности, из формулы (1.9) при помощи оператора Гамильтона, соблюдая правила применения последнего. Перепишем сначала (1.9) в виде:

(существен порядок сомножителей скалярных произведений). Полагая теперь  , имеем:
, имеем:
 ,
,
что совпадает с (5.12), если учесть (5.3) и (5.4).
С помощью оператора Гамильтона легко доказываются также другие полученные ранее тождества (4.4), (4.5):


Последнее равенство можно трактовать физически так: «вихрь не растекается».
5.3. Теорема Грина. Вернёмся к рассмотренной ранее теореме Остроградского-Гаусса. Положив  и учитывая, что согласно (5.9)
и учитывая, что согласно (5.9)
 ,
,
имеем из (3.8):
 (5.13)
(5.13)
Здесь применён оператор Гамильтона и учтено, что  Полученный результат выражает теорему Грина; равенство (5.13) называют также первой формулой Грина.
Полученный результат выражает теорему Грина; равенство (5.13) называют также первой формулой Грина.
Получим, далее, вторую формулу Грина. Для этого надо сначала переписать первую формулу Грина, поменяв в ней местами функции ψ и φ, а затем вычесть новое равенство из первоначального. В результате находим:

Поскольку полученные соотношения есть следствия теоремы Остроградского-Гаусса, то о границах применимости обеих формул Грина можно повторить всё сказанное выше в п. 1. В частности, векторные функции  и
и  должны быть однозначными; в противном случае требуется преобразование области интегрирования.
должны быть однозначными; в противном случае требуется преобразование области интегрирования.
