По курсу сопротивления материалов

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ

РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ

По курсу сопротивления материалов

Для студентов инженерного факультета заочного отделения, обучающихся по:

1) Направлениям подготовки23.03.03 «Эксплуатация транспортно-технологических машин и комплексов», 35.03.06 «Агроинженерия»;

2) Специальности 23.05.01 «Наземные транспортно-технические средства»

Чебоксары-2017

УДК 531.8

ББК 22.21

Рецензент:

Методические указания к выполнению расчетно-графической работы по курсу сопротивления материалов: Учебно-методическое пособие. /Сост. А.О. Васильев, У.В. Александрова.- Чебоксары: ФГБОУ ВО ЧГСХА, 2017. – 43 с.

В пособии приведены задания к расчетно-графической работе по сопротивлению материалов, показан пример ее выполнения. Кроме того, каждое задание сопровождается краткими указаниями в виде указаний к выполнению работы.

Сборник предназначен для обеспечения самостоятельной работы студентов очной формы обучения при изучении курса сопротивления материалов по:

1) Направлениям подготовки23.03.03 «Эксплуатация транспортно-технологических машин и комплексов», 35.03.06 «Агроинженерия»;

2) Специальности 23.05.01 «Наземные транспортно-технические средства».

Рекомендовано к изданию учебно-методическим советом ФГБОУ ВО ЧГСХА.

© ФГБОУ ВО ЧГСХА, 2017

© А.О. Васильев, У.В. Александрова, 2017

Общие методические указания

Основная цель выполнения расчетно-графических работ заключается в привитии навыков самостоятельного решения практических задач с одновременным закреплением теоретических знаний.

При рациональной организации выполнения расчетно-графических работ им предшествуют лекции и решение простых задач по соответствующей тематике.

Оформление расчетно-графической работы должно выполняться с соблюдением основных правил, установленных стандартами. К ним следует отнести:

-выполнение пояснительной записки на одной стороне листа формата А4 с рамкой по соответствующей форме;

-пояснение расчетов чертежами, схемами и рисунками, выпол­ненными в соответствии с ЕСКД;

-наличие ссылок на формулы, указание источника, из которого принимаются справочные данные, и т. п.;

-соблюдение правил записи и округления цифровых величин;

-указание размерностей;

-наличие титульного листа.

Методические указания для выполнения контрольных заданий.

Теоретические сведения к выполнению задач

Сведения к решению задачи 1

Растяжением или сжатием называется такой вид деформации, при котором в поперечном сечении стержня возникает один внутренний силовой фактор – продольная сила N.

Величина N равна алгебраической сумме проекций на продольную ось z всех внешних сил, действующих на отсеченную часть стержня

N=∑ F_KZ (3.1)

Так как величина продольных сил в разных сечениях стержня неодинакова, то строится эпюра продольных сил, т.е. график, показывающий изменения величины продольных сил в сечении стержня по его длине.

Под действием продольных сил в поперечном сечении стержня возникает нормальное напряжение σ, которое определяется по формуле:

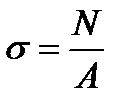, (3.2)

где А- площадь поперечного сечения стержня.

При решении первой задачи требуется умение строить эпюры продольных сил, нормальных напряжений и определять удлинение или укорочение стержня.

Последовательность построения эпюр продольных сил:

1. Разбиваем стержень на участки, ограниченные точками приложения сил (нумерацию участков ведём от незакрепленного конца ).

2. Используя метод сечений, определяем величину продольных сил в сечении каждого участка.

3. Выбираем масштаб и строим эпюру продольных сил, т.е. под изображением стержня проводим прямую, параллельную его оси, и от этой прямой проводим перпендикулярные отрезки, соответственно в выбранном масштабе продольным силам (положительное значение откладываем вверх, отрицательное – вниз.

Последовательность построения эпюр нормальных напряжений:

1. Разбиваем стержень на участки, ограниченные точками приложения сил и там, где меняется площадь сечения.

2. Строим эпюру нормальных сил.

3. По формуле (3.1) определяем нормальные напряжения на каждом участке.

4. По полученным значениям в масштабе строим эпюру нормальных напряжений.

Удлинение ( укорочение ) стержня определяется по формуле Гука

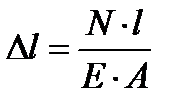, (3.3)

где Е – модуль Юнга(модуль упругости) ( для большинства конструкционных сталей E=2·10 ¹¹ Па),

l – Длина участка стержня, м.

Удлинение (укорочение) определяется на каждом участке стержня, а затем находят алгебраическую сумму полученных значений. Это будет ∆l стержня. Если ∆l положительна, то брус удлиняется, если ∆l отрицательна, то укорачивается.

При решении ряда задач необходимо ясно представлять смысл условия прочности при растяжении – сжатии, знать, что исходя из условия прочности, можно производить три вида расчётов:

а) проверочный, при котором проверяется выполнено ли условие прочности σ≤ [σ], где [σ] – предельно допускаемое нормальное напряжение, Па;

б) определение допускаемой нагрузки;

в) проектный, при котором определяются необходимые размеры поперечных сечений бруса, обеспечивающие заданную прочность.

Сведения к решению задачи 2

Статическими моментами относительно осей x и y плоской фигуры (рисунок 3.1) называются характеристики:

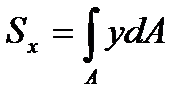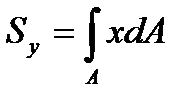, , (3.4)

где А – площадь фигуры,

х, у – координаты элементарной площадки dA.

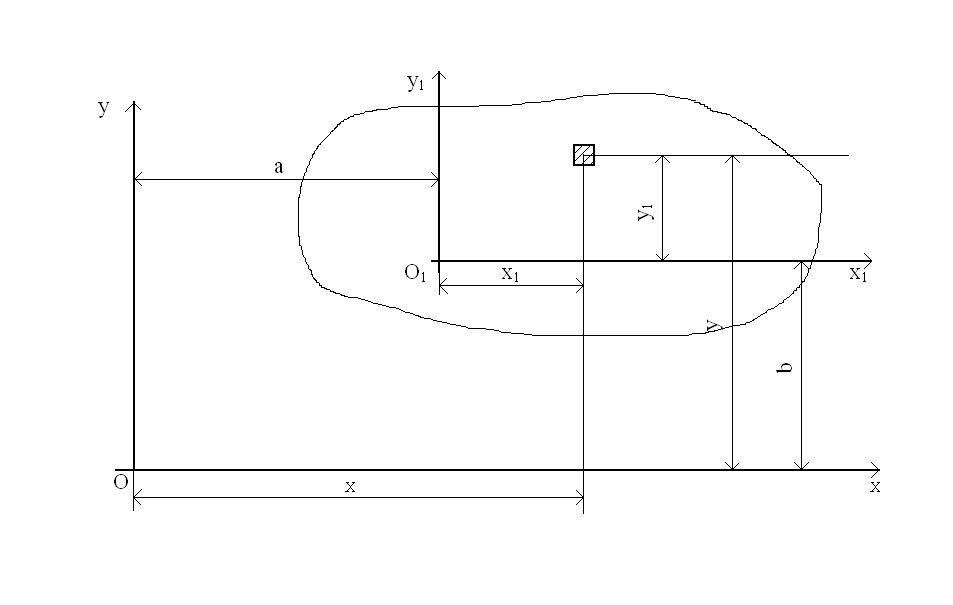
Рисунок 3.1 – К определению геометрических характеристик плоских фигур.

Единицей измерения статического момента являются единица длины в третьей степени, обычно [см³].

Осевыми моментами инерции плоской фигуры относительно осей х и у называются характеристики

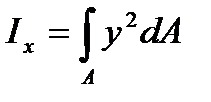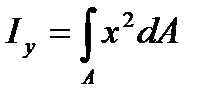, . (3.5)

Центробежным моментом инерции плоской фигуры называется характеристика

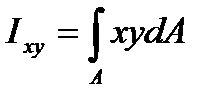. (3.6)

Полярным моментом инерции плоской фигуры называется характеристика

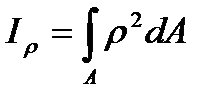. (3.7)

Моменты инерции измеряются в единицах длины в четвертой степени, обычно в [см⁴].

Осевые и полярный моменты инерции всегда положительны.

Центробежный момент инерции может быть положительным, отрицательным и равен нулю.

Если хотя бы одна из осей х или у является осью симметрии фигуры, то центробежный момент инерции .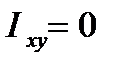

При параллельном переносе осей (рисунок 3.1) моменты инерции преобразуются:

,

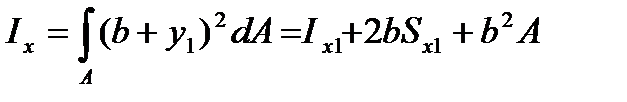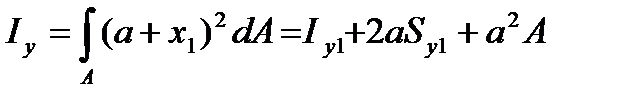, (3.8)

.

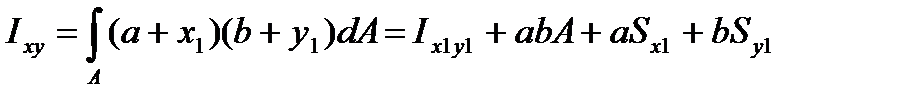Если точка 0₁- центр тяжести фигуры, то статические моменты S_х1 и S_у1 в (3.8) превращаются в нуль.

Главные оси инерции и главные моменты инерции.

Существует значение угла 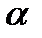наклона осей координат, при котором I_х1 и I_y1 принимают экстремальные значения. Он определяется общей формулой:

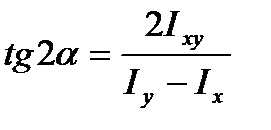. (3.10)

Эта формула определяет положение двух осей, относительно одной из которых осевой момент инерции максимален, а относительно другой - минимален.

Такие оси называются главными осями инерции фигуры. Моменты инерции относительно этих осей называются главными моментами инерции фигуры.

При этом центробежный момент инерции I_xy относительно главных осей инерции равен нулю.

Главные оси инерции, проходящие через центр тяжести сечения, называются главными центральными осями инерции. Ось симметрии – одна из главных центральных осей инерции.

После преобразований получим формулу для определения главных моментов инерции:

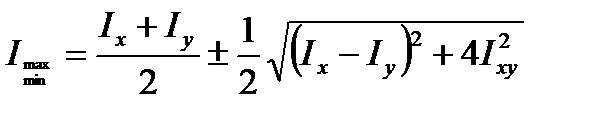. (3.11)

Радиусы инерции.

Характеристики

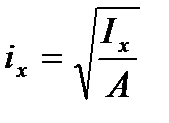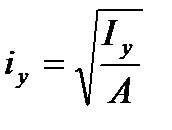, (3.12)

называются радиусами инерции плоского сечения.

Главным центральным осям инерции соответствуют главные радиусы инерции:

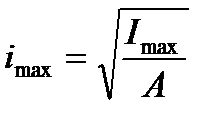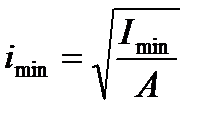, . (3.13)

При этом, какова бы ни была форма и величина плоского сечения и расположение ее масс, величины моментов инерции ее относительно различных осей, лежащих в плоскости фигуры и проходящих через заданную точку О , характеризуются некоторым эллипсом. Этот эллипс называется эллипсом инерции пластинки по отношению к точке О. Если точка О — центр тяжести пластинки, то этот эллипс называется ее центральным эллипсом инерции.

Эллипс инерции играет большую роль в механике, и особенно важное применение его имеет место в сопротивлении материалов. В сопротивлении материалов доказывается, что если мы имеем балку с каким-нибудь заданным сечением, то сопротивление ее изгибу будет пропорционально моменту инерции ее сечения относительно оси, проходящей через центр тяжести сечения и перпендикулярной к направлению изгибающей силы. Поясним это примером. Предположим, что мостик через ручей сделан из доски и доска прогибается под действием веса проходящего по ней пешехода. Если ту же доску (а не более толстую) положить «на ребро», она почти вовсе не прогнется, т. е. в положении «на ребро» доска прочнее. Это происходит от того, что у поперечного сечения доски, которое имеет форму довольно вытянутого прямоугольника, момент инерции I_x этого сечения относительно оси, лежащей в его плоскости, проходящей через его центр и перпендикулярной к его длинной стороне, больше, чем момент I_y относительно оси, проходящей параллельно его длинной стороне.

Если бы класть доску не в точности плашмя или на ребро, а косо, и даже если брать не доску, а брусок с любым сечением, то все же сопротивление изгибу будет пропорционально моменту инерции этого сечения относительно соответственной оси, лежащей в его плоскости и проходящей через его центр тяжести. Жесткость при изгибе балки, таким образом, характеризуется эллипсом инерции ее сечения.

Сведения к решению задачи 3

Деформация изгиба возникает в стержнях от действия нагрузки, направленной перпендикулярно оси стержня. Стержень, работающий на изгиб, называется балкой.

При изгибе в поперечных сечениях балки возникают две составляющих – поперечная сила Q_y и изгибающий момент M_x.

При построении эпюр Q_y и M_x в балке, она разбивается на участки, границами которых являются сечения, в которых приложены сосредоточенные силы или моменты, начинается либо кончается распределённая нагрузка. На каждом таком участке – свои Q_y и M_x.

Последовательность построения эпюр Q_y и M_x:

1. Определение опорных реакций из уравнений статики, их проверка.

2. Разбивка балки на участки.

3. Получение уравнений Q_y на первом участке.

4. Построение эпюры Q_y по значениям, вычисленным из уравнения.

5. Получение уравнения M_x на первом участке.

6. Построение эпюры M_x по значениям, вычисленным из уравнения.

7. Повторение пунктов 3-6 для остальных участков.

8. Проверка эпюр по общим закономерностям.

Для определения реакций опор необходимо:

Освободить балку от связей (опор) и изобразить действующие на неё заданные нагрузки. В данную расчетную схему включить неизвестные опорные реакции, векторы которых должны быть направлены перпендикулярно оси балки. Для неподвижной опоры следует дополнительно ввести опорную реакцию, вектор которой направлен вдоль оси балки. Направления векторов всех неизвестных опорных реакций на данном этапе расчета можно назначать произвольным образом.

Распределенную нагрузку необходимо заменить эквивалентной ей сосредоточенной силой, действующей в том же направлении и приложенной в центре тяжести эпюры распределенной нагрузки

Выбрать систему координат и составить уравнения равновесия. Начало координат удобнее совмещать с левым концом балки, за ось X принять ось балки. Представляется целесообразным составлять уравнения равновесия моментов относительно тех точек балки, в которых приложены неизвестные опорные реакции. При наличии внешней нагрузки, вызывающей горизонтальную составляющую у реакции в неподвижной опоре, необходимо добавить уравнение равновесия проекций действующих нагрузок, включая неизвестные опорные реакции, на горизонтальную ось балки.

Решить составленные уравнения равновесия. В случае отрицательных значений у вычисленных опорных реакций следует изменить направления соответствующих векторов на противоположные.

Проверить правильность полученных результатов по уравнению, которое не было использовано в ходе решения, путем подстановки в него вычисленных опорных реакций с учетом их уточненных направлений.

При записи выражений для Q_y и M_x следует придерживаться определенных правил:

• поперечная сила численно равна алгебраической сумме внешних сил, действующих по одну сторону от рассматриваемого сечения. Внешняя сила дает положительное слагаемое, если стремится повернуть оставшуюся часть балки относительно данного сечения по часовой стрелке. Следует мысленно установить шарнир в рассматриваемом сечении, относительно которого поворачивается отсеченная часть балки от действующих сил;

• изгибающий момент численно равен сумме моментов относительно рассматриваемого сечения от всех нагрузок, действующих по одну сторону от этого сечения. Момент от нагрузки считается положительным, если вызывает сжатие верхних волокон рассматриваемой части балки. Мысленно установить в этом сечении заделку и рассмотреть состояние верхних волокон отсеченной части балки в зависимости от данного вида нагрузки.

Графически правило знаков для поперечных сил Q_y и изгибающих моментов M_x в зависимости от движения к сечению показано на рисунке 3.2.

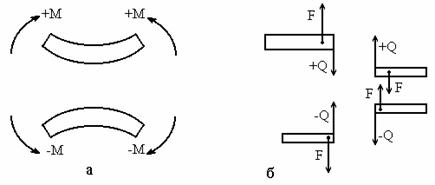
Рисунок 3.2 – Правило знаков: а) для изгибающих моментов; б) – для поперечных сил.

По вычисленным значениям поперечных сил и изгибающих моментов построить в масштабе соответствующие эпюры. Положительные значения откладывать от нулевой линии вверх, отрицательные – вниз. Полученные плоские фигуры заштриховать вертикальными линиями с указанием знаков.

Подбор сечения балки (проектный расчет) выполняется по методу допускаемых напряжений.

Особенностью расчета изгиба консольных балок является отсутствие необходимости определения опорных реакций. В этом случае определение поперечных сил Q_y и изгибающих моментов M_x целесообразно начинать от свободного торцевого сечения.

При поперечном изгибе в сечении бруса возникают и касательные напряжения. На основании закона парности касательных напряжений последние возникают также и в продольных сечениях, вызывая сдвиги отдельных волокон относительно друг друга.

Для определения напряжений 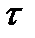надо знать закон их распределения по ширине балки. Для большинства поперечных сечений делается допущение, что напряжения 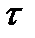распределены равномерно по ширине сечения, т.е. на любой прямой, параллельной оси x (гипотеза Журавского). Касательные напряжения при изгибе определяются по формуле

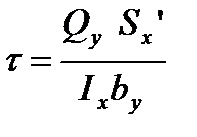, ( 3.14)

где Q_y – поперечная сила в сечении балки, Н.

S`_x – статический момент части балки, находящейся выше той точки, в которой определяются касательные напряжения, м³;

I_x – осевой момент инерции фигуры, м⁴.

b_y - ширина поперечного сечения балки в той точке, в которой определяются касательные напряжения, м.

Выражение (3.14) называют формулой Журавского, который впервые установил наличие касательных напряжений при изгибе.

Примеры решения задач

Пример решения задачи 1

Для заданного ступенчатого бруса:

1. Построить эпюру продольных сил.

2. Определить минимально допустимые размеры поперечного сечения, если 1 участок имеет круглое сечение, и 2 участок – прямоугольное сечение со сторонами b и h. Результаты принять в соответствии с сортаментом согласно ГОСТ.

3. Определить полную абсолютную деформацию бруса и построить эпюру перемещений.

4. Определить полную потенциальную энергию деформации всего бруса.

Исходные данные:

F1, кН	F2, кН	ℓ1, м	ℓ2, м

Указания:

Модуль упругости материала: Е=2·10⁵ МПа;

Предельно допускаемое напряжение растяжения [σ_p]=160 МПа;

Предельно допускаемое напряжение сжатия [σ_с]=120 МПа;

Соотношение сторон прямоугольного сечения второго участка:h/b=3;

Рисунок 3.3 – Эпюры продольных сил и перемещений в стержне.

1. Строим график (эпюру) продольных сил :

Построение эпюры ведем со свободной стороны стержня.

Первый участок: N₁=-F₁=-24 кН;

Второй участок: N₂=-F₁+F₂=-24+40=16 кН.

2. Определяем размеры поперечного сечения из условия прочности:

Условие прочности:

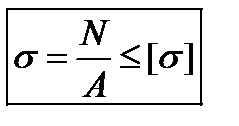
Первый участок сжат, так как продольная сила на этом участке эпюры имеет отрицательное значение. Поэтому для решения по условию прочности выбираем значение [σ_с].

Минимально допустимая площадь первого участка:

;

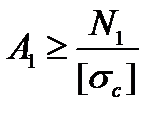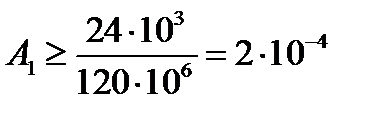м²=200 мм².

Поскольку сечение первого участка круглое, то его площадь равна

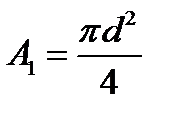, отсюда получаем минимально допустимый диаметр круглого изделия:

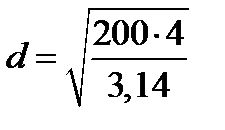=15,96 мм.

Согласно ГОСТ выбираем прокат круглого сечения с округлением в большую сторону: d=16 мм.

Тогда с учетом округления площадь первого участка

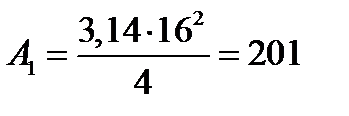мм².

Второй участок растянут, т.к. на этом участке продольная сила имеет отрицательное значение. Поэтому для решения по условию прочности выбираем значение [σ_р].

Минимально допускаемая площадь второго участка:

;

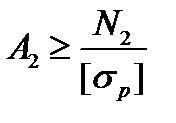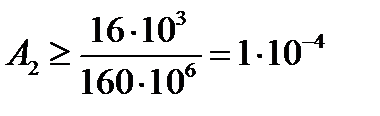м²=100 мм².

Поскольку сечение второго участка прямоугольное с соотношением сторон h/b=3, его площадь равна

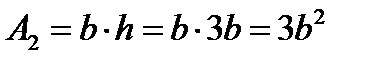, отсюда получаем минимально допустимую ширину прямоугольного изделия:

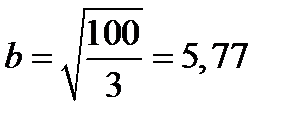мм.

Согласно ГОСТ выбираем полосу с округлением в большую сторону: b=6 мм и отрезаем на величину h=3b=18 мм.

Тогда с учетом округления площадь первого участка

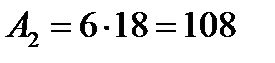мм².

3. Построим эпюру перемещений.

За начало отсчета выбираем неподвижную точку А с закрепленной стороны стержня. Удлинение (укорочение) стержня определяется по формуле Гука (3.3).

Перемещение точки А:

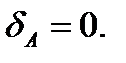
Перемещение точки В:

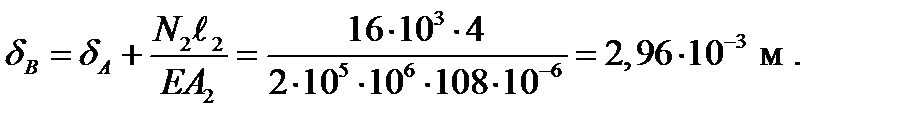
Перемещение точки С:

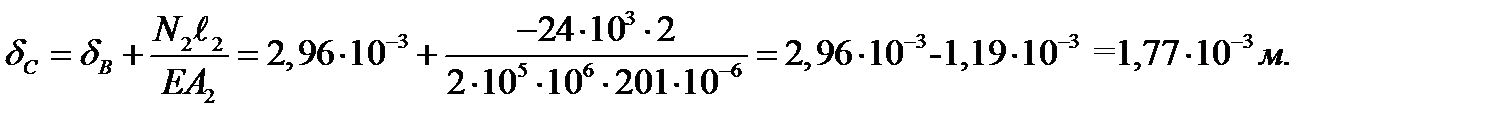
Перемещение точки С соответствует полной абсолютной деформации всего бруса.

4. Определяем полную потенциальную энергию деформации всего бруса.

Для этого считаем потенциальную энергию деформации на каждом участке:

;

;

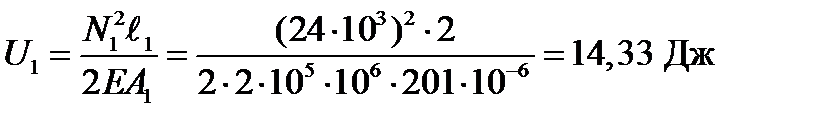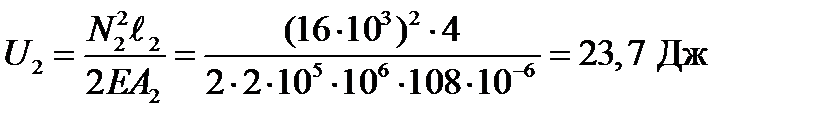Полная потенциальная энергия:

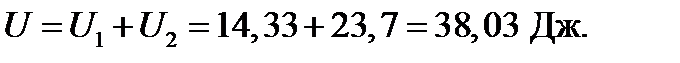
Пример решения задачи 2

1. По данным таблицы определить центр тяжести сечения.

2. Определить центральные моменты инерции: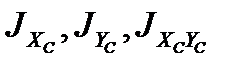

3. Вычислить главные моменты инерции 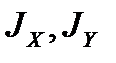, а также угол наклона главных осей инерции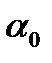

4. Вычислить главные радиусы инерции и построить эллипс инерции.

Исходные данные к примеру 2.

ГОСТ 8509-72 уголок равнополочный	ГОСТ 8510-72 уголок неравнополочный	Расстояние а, см
125×125×8	110×70×8

Составляем для удобства таблицу исходных данных, которую заполняем, используя соответствующий сортамент из справочников.

ГОСТ 8509-72 Уголок 1	ГОСТ 8510-72 Уголок 2	Расстояние а, см
125×125×8	110×70×8	2,0
b2=12,5 см	B1=11 см
	b1=7 см
t2 = 0,8 см	t1 = 0,8 см
А2 = 19,7 см2	А1 = 13,93 см2
Iу = Ix = 294,36 см4	Ix = 171,54 см4
	Iу = 54,64 см4
z0 = 3,36 см	х0 = 1,64 см
Imax = 467 см4	у0 = 3,61 см
Imin = 122 см4	tgα=0,4

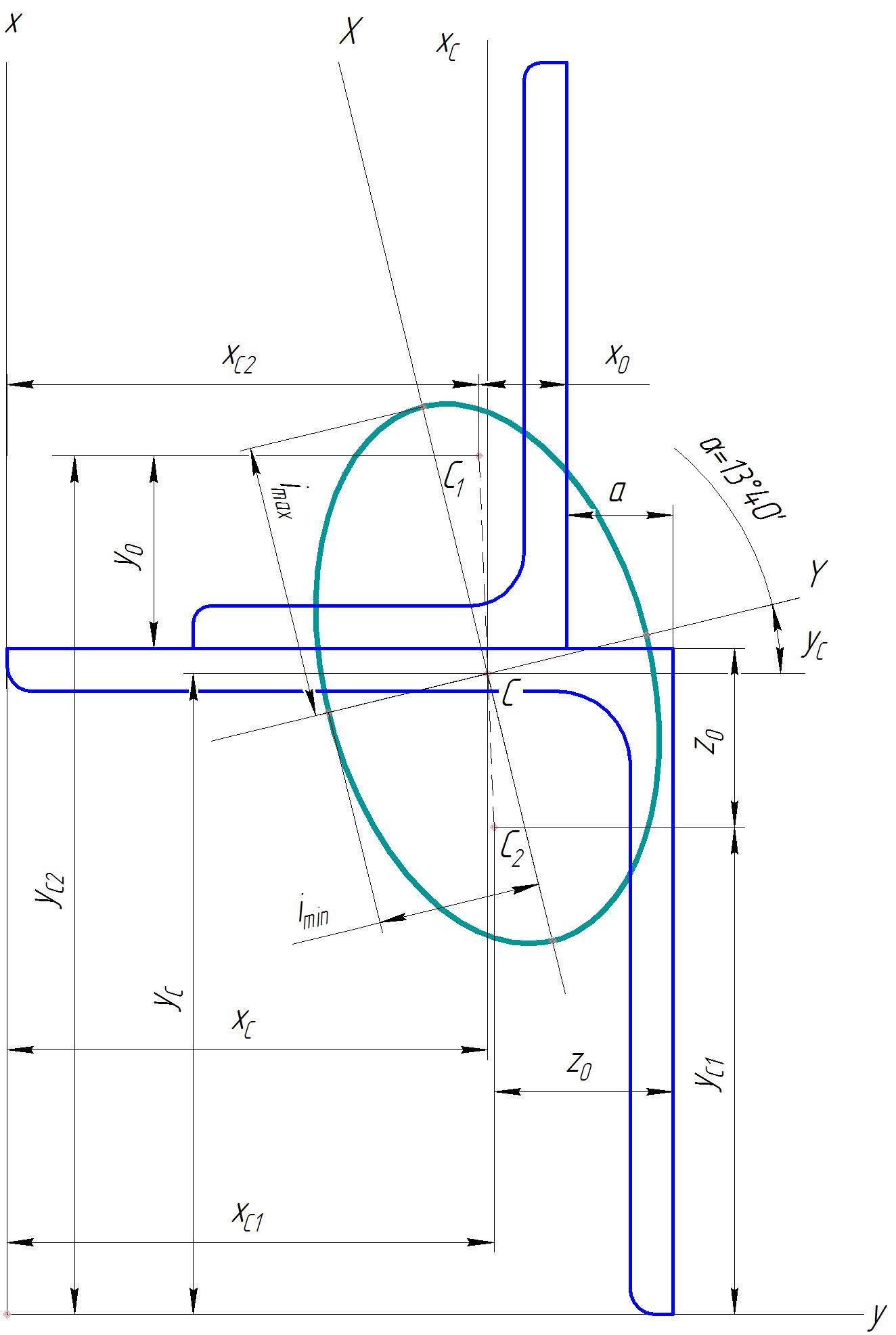
1.Определим координаты центра тяжести сечения. Для этого проведем координатные оси х и у касательно к контуру сечения, чтобы площадь всего сечения находилась в первой четверти системы координат. Пронумеруем составляющие сечение фигуры: 1 – равнополочный уголок, 2 – неравнополочный уголок.

С помощью таблиц сортамента ГОСТ 8509-86 и ГОСТ 8510-86, а также учитывая расположение уголков, определим положение центров тяжести C₁ и С₂ для каждой из фигур (глядя на схему):

Уголок 1:

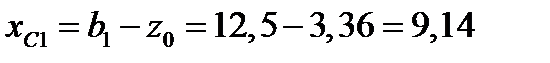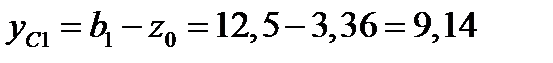см.

см.

Уголок 2:

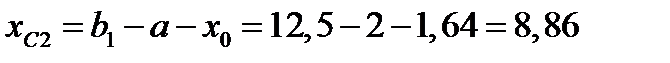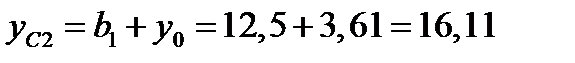см.

см.

Координаты центра тяжести всей фигуры

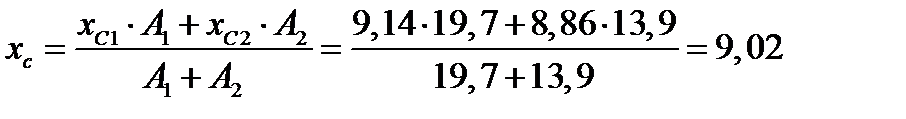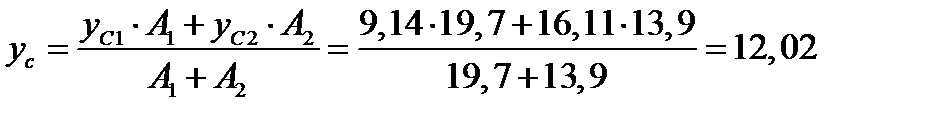см.

см.

Наносим точку С на схему.

2. Определяем центральные моменты инерции всей фигуры.

Для этого через точку С проводим центральные оси x_C и y_C и находим осевые и центробежный момент инерции сечения этих осей. При этом следует пользоваться таблицами сортамента, обращая внимание на расположение уголков.

Центральный и центробежный моменты инерции всей фигуры относительно осей x_C и y_C определяются согласно методике расчета соответствующих моментов инерции при переносе координатных осей.

Центральный момент инерции относительно оси x_C:

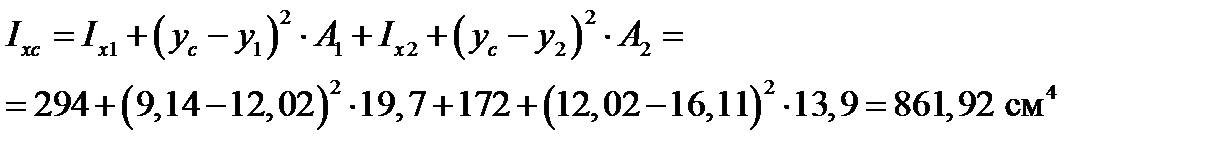
Центральный момент инерции относительно оси y_C:

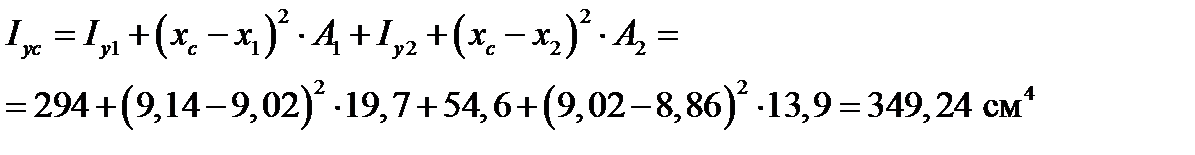
Центробежный момент инерции определяется по формуле:

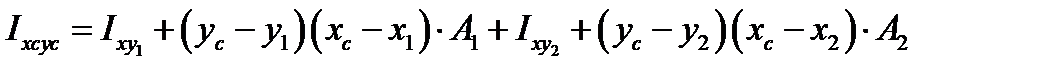
Однако эта формула содержит неизвестные величины 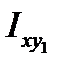и 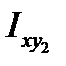, которые можно найти несколькими путями:

а) воспользоваться расширенными таблицами сортамента.

б) рассчитать по формулам, исходя из имеющихся значений по следующей методике с учетом правила знаков:

Если уголок расположен на схеме в соответствии с направлением 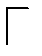или 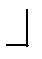, то ставится знак «+», а если уголок расположен в соответствии с направлением 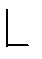или 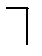, то ставится знак «-»

Для равнополочного уголка

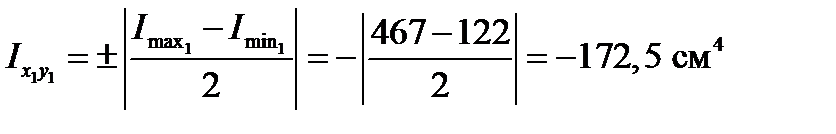
Для неравнополочного уголка

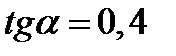- по таблице.

Отсюда ,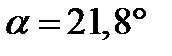

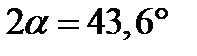, поэтому

.

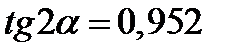
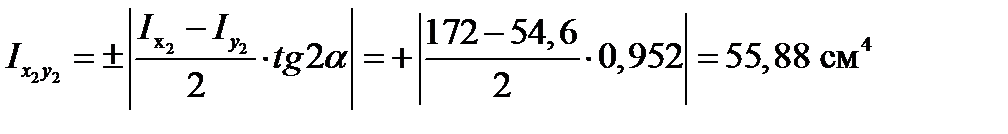Окончательно получаем:

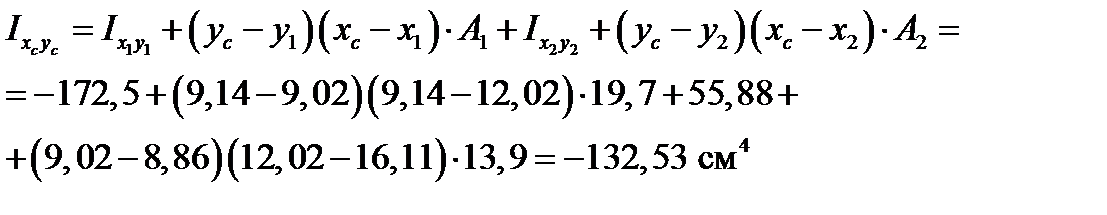
Следует помнить, что значения 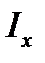и 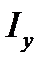принимают только положительные значения, а 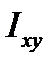может быть положительным, отрицательным и равным нулю.

3. Определяем главные моменты инерции всей фигуры.

Главными моментами инерции плоской фигуры являются те, которые принимают максимальное и минимальное значение относительно осей, проведенных под углом наклона 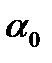. Значения главных моментов инерции всей фигуры определяется общей формулой:

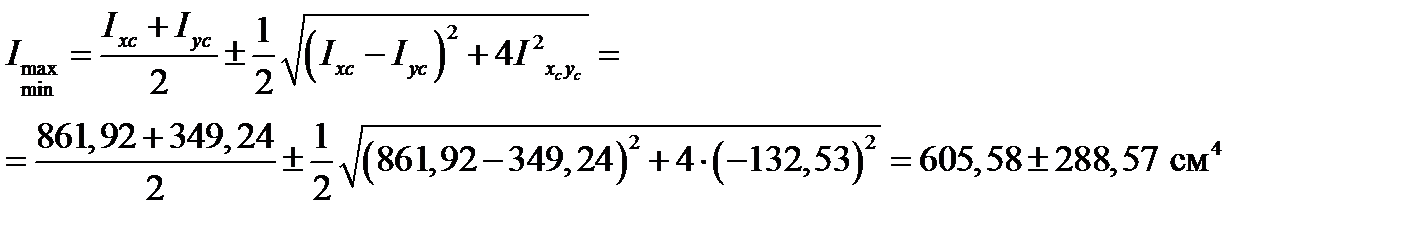
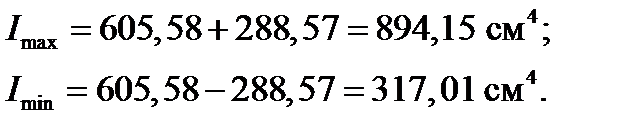
Проверка: ;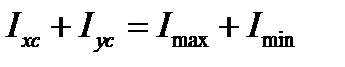

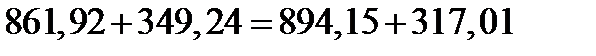
Угол наклона главных осей определяется по общей формуле:

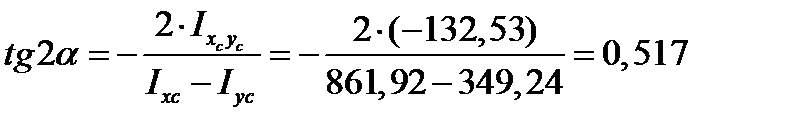
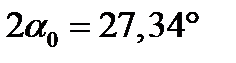
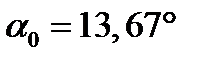
Поду углом 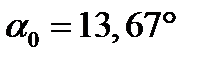через точку С проводим оси Х и Y – главные оси.

4. Определяем главные радиусы инерции и по полученным данным строим эллипс инерции. Длина полуосей эллипса инерции соответствует радиусам инерции всей фигуры. При этом, если 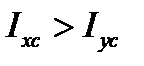, то бόльшая полуось эллипса 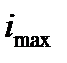откладывается на оси Y, а меньшая 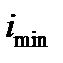на оси Х.

.

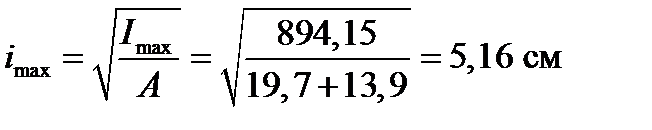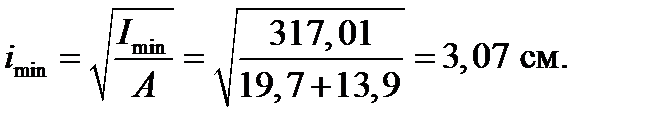
Пример решения задачи 3

Произвести расчет на прочность при изгибе. Для этого:

1. Построить эпюры поперечных сил Q_y и изгибающих моментов M_x.

2.Подобрать сечение двутавровой балки по нормальным напряжениям при [σ]= 160 MПa.

3.Для сечения балки, в котором изгибающий момент M_x достигает наибольшего значения, построить эпюры нормальных и касательных напряжений.

Данные к задаче:

m кНм	Р кН	g кН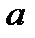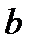/м		м	м	м
30	20	20	1,0	1,5	1,2

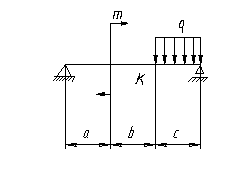
РЕШЕНИЕ:

1. Построим эпюры поперечных сил Q_y и изгибающих моментов М_х.

Для этого определяем силы реакции опор балки исходя из уравнений равновесия.

∑М_А = 0:

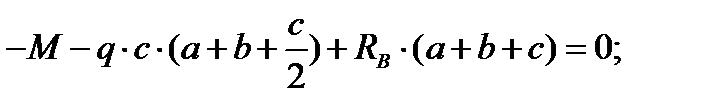
Отсюда

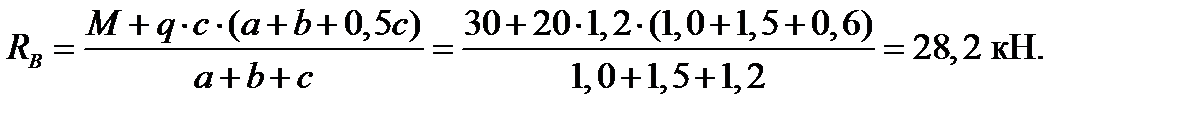
∑М_В = 0:

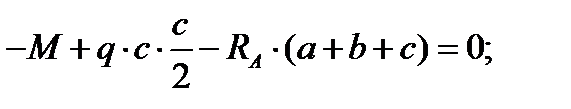
Отсюда

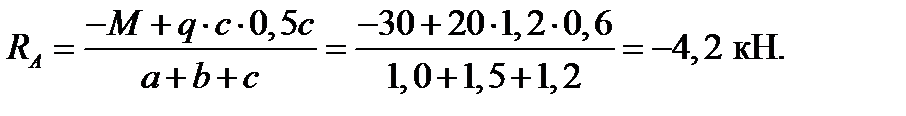
Проверка:

∑F_ky = 0:

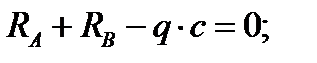
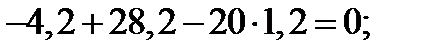- решение верное.

Разбиваем балку на участки.

Рассмотрим сечение 1 – 1, на расстоянии z₁, в котором:

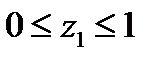
Поперечная сила в сечении 1-1:

Q_y = R_A = -4,2 кН.

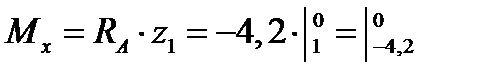
Рассмотрим сечение 2 – 2:

0 ‹ z₂ ‹ 1,5

Q_y = R_A =-4,2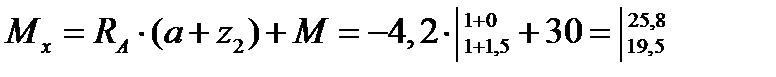кН.

кН;

Рассмотрим сечение 3 – 3:

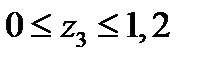
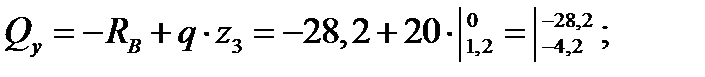
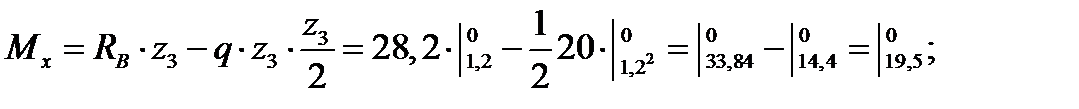
Полученные значения наносим на соответствующие эпюры в произвольно выбранном масштабе (Рисунок 3.1).

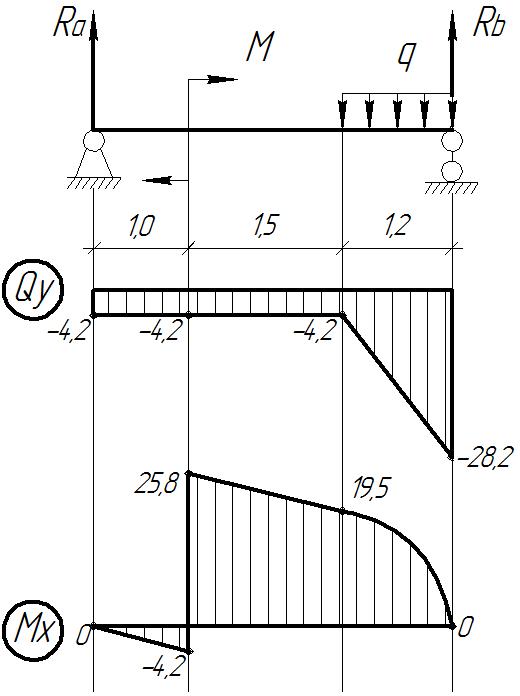
Рисунок 3.1 – Эпюра поперечных сил Q_y и изгибающих моментов M_x.

Из построенной эпюры M_x видно, что максимальное значение изгибающего момента М_х^max = 25,8 кН ∙ м; при этом Q_y = -4,2 кН.

2. Подбираем сечение двутавровой балки по нормальным напряжениям при [σ] = 160 МПа.

,

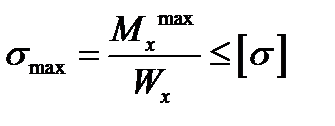где W_x – момент сопротивления двутавровой балки, см³. Его значение можно найти в соответствующей таблице сортамента.

;

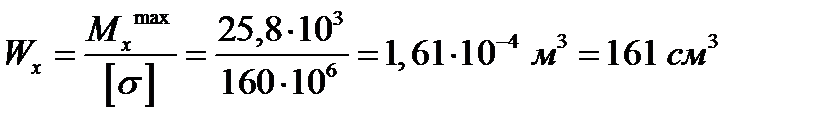Находим в таблице сортамента для двутавровых балок значение, ближайшее к получившемуся с округлением в бόльшую сторону.

Ему соответствует W_x = 184 см³ – что соответствует двутавровой балке №20.

Переписываем для удобства некоторые характеристики выбранного двутавра из таблицы:

h = 20 см = 0,2 м.

b = 10 см = 0,1 м.

s = 0,52 см = 0,52·10^-2 м.

t = 0,84 см = 0,84·10^-2 м.

S_x^max = 104 см² = 104·10^-6 м³.

I_x=1840 см⁴=1840·10^-8 м⁴.

Также в сечении двутавра можно выделить следующие величины:

S_x^ст – статический момент стенки половины двутавра, которую можно принять за прямоугольник;

S_xⁿ – статический момент полки, который равен:

.

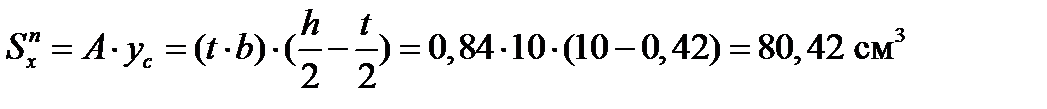3. Для сечения балки, в котором изгибающий момент M_x достигает наибольшего значения, построим эпюры нормальных и касательных напряжений.

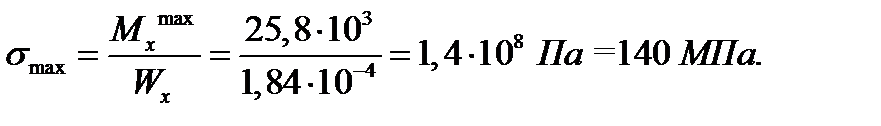‹ 160 МПа

.

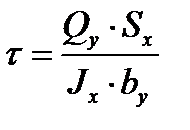
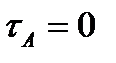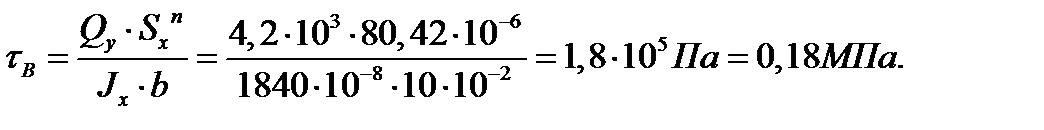
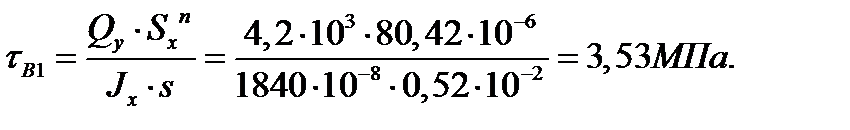
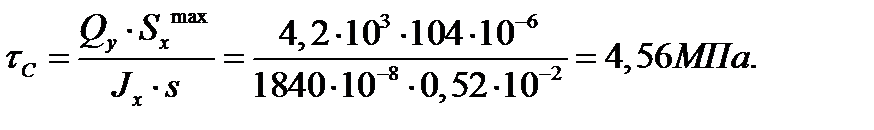
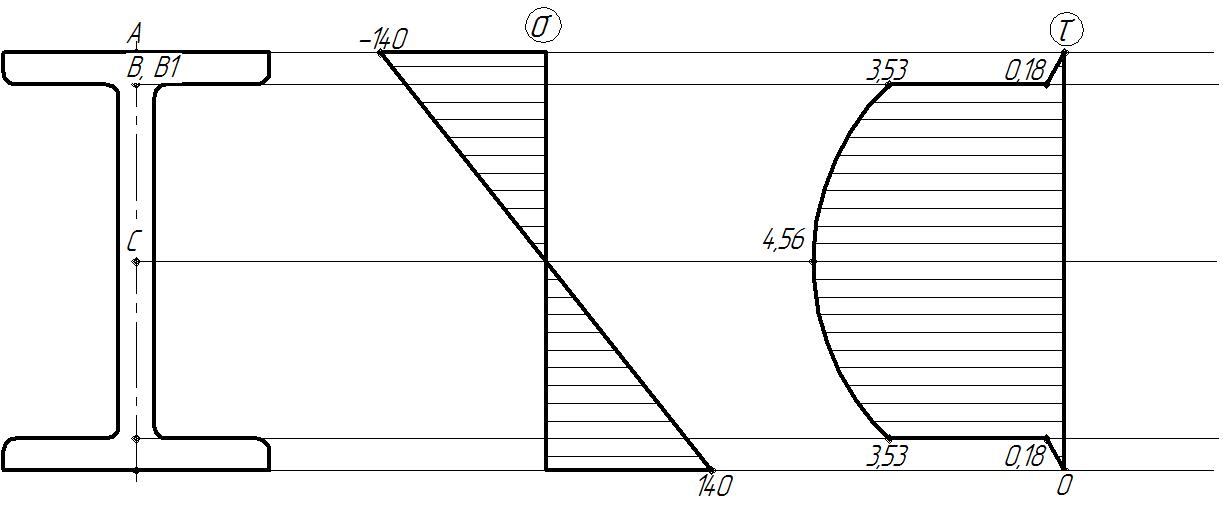
Рисунок 3.2 – Эпюра нормальных и касательных напряжений в поперечном сечении двутавровой балки.

Вопросы для самопроверки.

Список рекомендуемой литературы

Оглавление

Общие методические указания................................................................. 3

1. Общие методические рекомендации по изучению дисциплины............ 4

1.1. Цели и задачи курса.............................................................................. 4

1.2. Компетенции обучающегося, формируемые в результате освоения дисциплины 5

2. Контрольные задания.............................................................................. 6

3. Методические указания для выполнения контрольных заданий. Примеры решения задач................................................................................................................ 16

4. Вопросы для самопроверки.................................................................... 40

5. Список рекомендуемой литературы....................................................... 41

Методические указания

к выполнению расчетно-графических работ по курсу сопротивления материалов. (сост. А.О. Васильев, У.В. Александрова)

Учебно-методическое пособие

Формат 60 х 84/16. Бумага писчая. Печать оперативная.

Усл. печ. л. 3,4. Тираж 100 экз. Заказ №

Федеральное государственное бюджетное образовательное учреждение высшего образования «Чувашская государственная сельскохозяйственная академия»

Отпечатано в полиграфическом отделе ФГБОУ ВО ЧГСХА , 428003, г.Чебоксары, ул.К.Маркса, 29.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ

РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ

по курсу сопротивления материалов

Для студентов инженерного факультета заочного отделения, обучающихся по:

1) Направлениям подготовки23.03.03 «Эксплуатация транспортно-технологических машин и комплексов», 35.03.06 «Агроинженерия»;

2) Специальности 23.05.01 «Наземные транспортно-технические средства»

Чебоксары-2017

УДК 531.8

ББК 22.21

Рецензент:

Методические указания к выполнению расчетно-графической работы по курсу сопротивления материалов: Учебно-методическое пособие. /Сост. А.О. Васильев, У.В. Александрова.- Чебоксары: ФГБОУ ВО ЧГСХА, 2017. – 43 с.

В пособии приведены задания к расчетно-графической работе по сопротивлению материалов, показан пример ее выполнения. Кроме того, каждое задание сопровождается краткими указаниями в виде указаний к выполнению работы.

Сборник предназначен для обеспечения самостоятельной работы студентов очной формы обучения при изучении курса сопротивления материалов по:

1) Направлениям подготовки23.03.03 «Эксплуатация транспортно-технологических машин и комплексов», 35.03.06 «Агроинженерия»;

2) Специальности 23.05.01 «Наземные транспортно-технические средства».

Рекомендовано к изданию учебно-методическим советом ФГБОУ ВО ЧГСХА.

© ФГБОУ ВО ЧГСХА, 2017

© А.О. Васильев, У.В. Александрова, 2017

Общие методические указания

Основная цель выполнения расчетно-графических работ заключается в привитии навыков самостоятельного решения практических задач с одновременным закреплением теоретических знаний.

При рациональной организации выполнения расчетно-графических работ им предшествуют лекции и решение простых задач по соответствующей тематике.

Оформление расчетно-графической работы должно выполняться с соблюдением основных правил, установленных стандартами. К ним следует отнести:

-выполнение пояснительной записки на одной стороне листа формата А4 с рамкой по соответствующей форме;

-пояснение расчетов чертежами, схемами и рисунками, выпол­ненными в соответствии с ЕСКД;

-наличие ссылок на формулы, указание источника, из которого принимаются справочные данные, и т. п.;

-соблюдение правил записи и округления цифровых величин;

-указание размерностей;

-наличие титульного листа.