Проддольный поперечный и скручивающий удар. Понятие об усталостной прочности

В случае продольного растягивающего или сжимающего удара

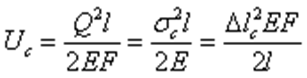
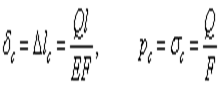
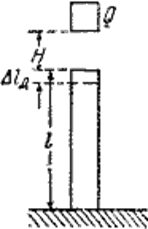
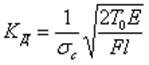
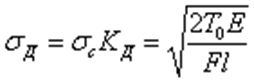
как при статической, так и при динамической нагрузке напряжение в сжатом стержне зависит от величины сжимающей силы и от площади поперечного сечения стержня.При изгибевеличина статической деформации 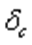, представляющей собой статический прогиб балки 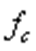с в месте удара, зависит от схемы нагружения и условий опирания балки. Так например, для балки пролетом l, шарнирно закрепленной по концам и испытывающей посредине пролета удар от падающего с высоты Н груза Q

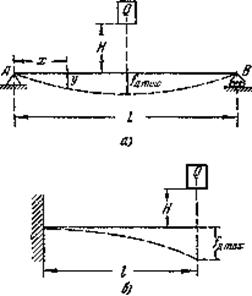
53. Циклические напряжения. Основные параметры цикла. Кривая усталости.Рассмотрим вначале случай одноосного напряженного состояния.Закон изменения главного напряжения о во времени представлен кривой, показанной нНаибольшее и наименьшее напряжения цикла обозначим через 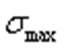и 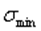. Их отношение называется коэффициентом цикла 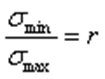В случае, когда 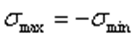, 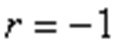и цикл называется симметричным Для испытаний в условиях несимметричных циклов используются либо специальные машины, либо же вводятся дополнительные приспособления. Так, например, можно на испытуемом образце установить пружину, создающую постоянное растяжение образца с напряжением 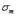. Во время испытания на это напряжение накладывается напряжение от изгиба, меняющееся по симметричному циклу.

54. Диаграмма предельных амплитуд. Факторы, влияющие на величину предела усталости. Расчёт на прочность при переменных напряжениях (диаграмма Серенсена-Кинасошвили).Диаграмма предельных амплитуд.

Диаграмма Хейга-Зодерберга

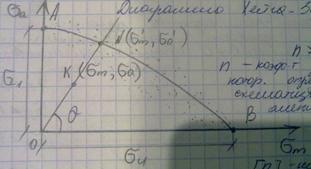
n >= [n] , n – коэффициент запаса, который определяется по схематизированной диаграмме амплитуд; [n] – нормативный коэффициент запаса (смотреть в справочник).

Циклы у которых максимальные напряжения равны пределу усталости называются предельными. 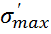= 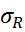, 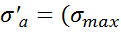- 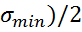– амплитуда цикла, 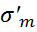=( 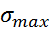+ 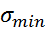)/2 - среднее напряжение; tgθ= 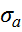/ 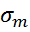= 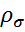- характеристика цикла, 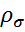= 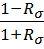, 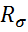-коэф асимметрии цикла, 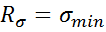/ 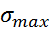, 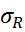- предел усталости цикла, n=ON/OK= 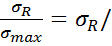( 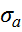+ 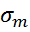). Диаграмму схематизированную строить удобно так как надо предельные σ.

Факторы, влияющие на величину предела усталости.

1.Эффективный коэффициент концентрации: 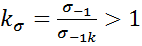- отношение предела усталости гладкого образца без концентратора к пределу усталости образца с концентратором.

2.Коэффициент поверхностной чувствительности: 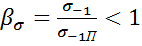- отношение предела усталости образца с рабочей поверхностью к пределу усталости полированного образца.

3.Масштабный коэффициент: 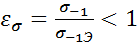- отношение предела усталости рабочей детали к пределу усталости этолонного образца 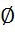6-12мм.

Расчёт на прочность при переменных напряжениях (диаграмма Серенсена-Кинасошвили).

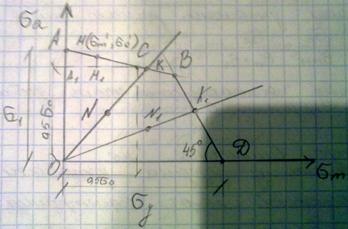
т. А( 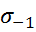) – симметричный цикл,

т. Д( )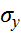

т. С( 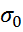) – отнулевой цикл.

ΔАСС₁∞ΔМСМ₁, АА₁/ММ₁=А₁С/М₁С, 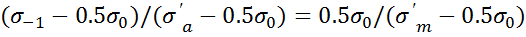, 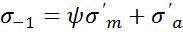- уравнение прямой, 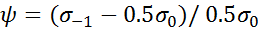- для идеального образца, 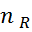- коэффициент запаса по усталостному разрушению,

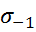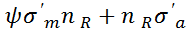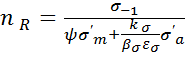= , . Для идеального цикла N можно записать: n=OK/ON , n=OK₁/ON₁ .

7. Статически неопределимые задачи при растяжении, сжатии: а) статически неопределимый брус; б)температурные напряжения; в)стержневые системы.

Стат. неопред. задачи имеют место, когда усилие и опорные реакции нельза определить только при помощи ур-я статики.Порядок расчёта:1) Статическая сторона задачи ( -записываем возможные ур-я статики; -опред-я степень стат. Неопределимости S=h-c, c – ур-е статики) 2)Геометр. сторона задачи (-строится план деформации сис-ы и нах-ся связь между деформацией). 3)Физическая сторона задачи (∆l – заменяем через усилие по з. Гука -∆l_i= 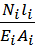) 4) Синтез (решаем совместно ур-я статики и деформации,(с учетом з. Гука) и находим неизв-е.Статически неопределимый брус

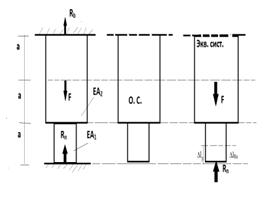
∑z=0 R_n+R_b=F S=2-1=1

Выбираем осн. сист.(для бруса)

Осн. система по S – это стат-и опред-й брус, полученный из заданного путём отбрасывания лишней связи. На основании принципе независимости действия сил получим: ∆l=∆l_F+∆l_Rn=0

∆l_F=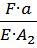

∆l_Rn=- 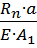- 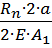= - = 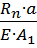R_n∙( ) =

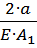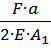
2R_n=F/2

R_n=F/4

Температурные напряжения

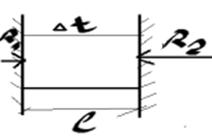R₁=R₂=R

∆l_t=α∙l∙∆t⁰

α – центр линейного расшир.

материала.

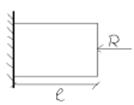
∆l_Rn = 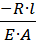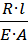= α∙l∙∆t⁰

∆l_Rn=∆l_Rt

∆l_Rt + ∆l_R =0 R= α∙∆t⁰∙E∙A

Ϭ=R/A= α∙E∙∆t⁰ Если есть зазор

∆l=∆