Каноническое разложение случайной функции в дискретном ряде точек

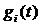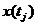Вид функции , который определен (5.42), приводит к мысли, что в качестве независимых случайных величин можно выбрать значения самой функции или их линейные комбинации. Зададим произвольную последовательность значений аргумента 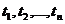и определим случайные величины по формуле

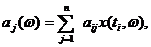(5.46)

где 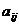- некоторые неизвестные, но не случайные коэффициенты. Коэффициент корреляции 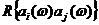определяется выражением

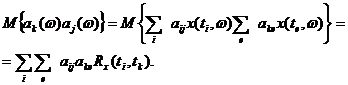(5.47)

Из формулы (5.40) следует, что 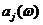и 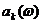не коррелированны и, следовательно, неизвестные коэффициенты должны удовлетворять условию

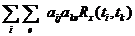=0 при 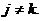(5.48)

Обозначим: 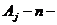мерный вектор- столбец с элементами 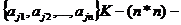мерную матрицу с элементами 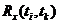. Выражение (5.48) может быть записано в матричных обозначениях, как 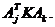Это выражение называется билинейной формой матрицы К в силу свойств корреляционной функции (см. п. п. 4.1) является симметрической и положительно определенной. Для таких матриц справедливы следующие свойства, которые мы приведем без доказательств [7].

Свойство 1.Все собственные числа симметрической матрицы с действительными элементами – действительные.

Свойство 2. Собственные векторы действительной симметрической матрицы, соответствующие различным собственным значениям, ортогональны между собой.

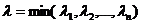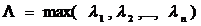Свойство 3. Пусть К- действительная симметрическая матрица и , где 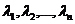- все собственные значения матрицы. Тогда для любого вектора z справедливо неравенство

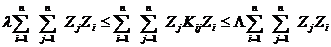. (5.49)

Свойство 4.Любая симметрическая положительно определенная матрица К может быть представлена в ви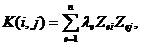де ,где 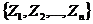ортонормированные собственные векторы, а 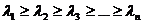- собственные числа матрицы К. В частности, .

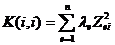В силу перечисленных свойств матрицы К, ее собственных векторов 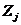и собственных чисел 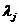ясно, что в (5.46) коэффициенты можно выбрать так, что 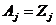. В этом случае легко убедиться в следующем:

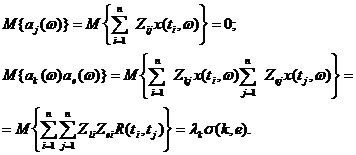(5.50)

Следовательно, при таком выборе 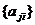дисперсии случайных коэффициентов 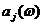равны 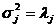. Получим для координатной функции

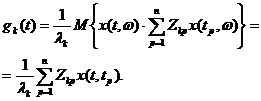(5.51)

В силу независимости коэффициентов 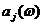легко разложить суммарную погрешность представления случайной функции в точках 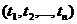на компоненты. Имеем 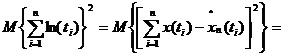(5.52)

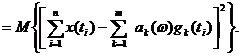
Возведем в квадрат выражение под знаком суммы:

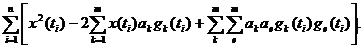(5.53)

Подставим 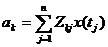во второй член (5.53) и получим:

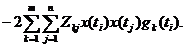(5.54)

Математическое ожидание от (5.54) равняется с учетом (5.51):

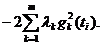(5.55)

Возьмем теперь математическое ожидание от (5.53). Учитывая (5.55), получим

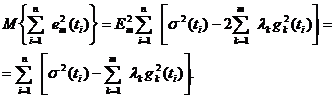(5.56)

В последнем выражении по определению 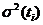= 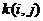и в силу свойства 4 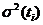= 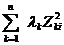. Второй член (5.56) легко приводится к виду 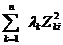. Окончательно получим, используя ортонормированность векторов :

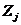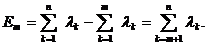(5.57)

Таким образом, видно, погрешность представления случайной функции x(t) в дискретных точках 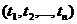полностью определяется собственными числами корреляционной матрицы К. В частности, 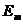= 0, если взять число функций, равных числу узлов, и 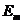> 0 в случае m < n. Равенство (5.57) позволяет проверить точность представления случайной функции рядом (5.43). Напомним , что речь идет о точности представления функции 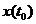только в узлах 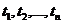. В общем случае погрешность (5.57) вычислить значительно сложнее [6].