Моменты конечномерных распределений случайных функций

Пусть 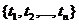- некоторый набор значений аргумента 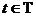. Этому набору соответствует система случайных величин .

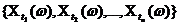Пусть при каждом 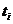функция распределения 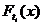дифференцируема, т. е. существуют соответствующие плотности вероятности 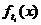. В данном случае исчерпывающей характеристикой этой системы является совместная плотность вероятности 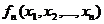, где для простоты обозначено 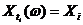. Очевидно, что если набор точек 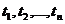исчерпывает (в случае дискретного 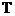) множество 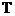, ансамбль случайных функций полностью описывается совместной плотностью вероятности 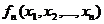. Значительно более сложно получить исчерпывающее представление случайной функции, если множество 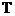содержит бесконечное число элементов. В этом случае любой конечный набор точек 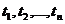является лишь некоторым подмножеством .

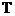Определение 1.2.

Семейство всех совместных распределений для n=1,2,… и всех возможных наборов значений 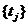называется семейством конечномерных распределений случайного процесса.

Семейство конечномерных распределений является одним из основных понятий теории случайных функций и в значительной степени определяет многие существенные их свойства.

К сожалению, имеются значительные практические трудности в реальном использовании этих семейств для конкретных случайных функций. Существует два общепринятых способа преодоления этих трудностей. Суть первого способа – рассмотрение только тех процессов, в которых любая плотность вероятности n-го порядка имеет определенную структуру может быть получена на основе плотностей вероятностей низшего порядка.

Второй способ заключается в преднамеренном ограничении допустимых операций над случайными функциями, которые могут быть изучены без фактически полного представления (задания) случайной функции. Для таких операций достаточно лишь частичное задание случайной функции. В данном случае вместо многомерных законов распределений ограничиваются рассмотрением соответствующих числовых параметров этих законов.

В качестве числовых параметров конечномерных распределений можно выбирать различные величины, однако наиболее удобными являются начальные и центральные моменты различных порядков. Напомним на примере двумерного случайного вектора 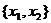с плотностью вероятности 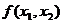, что смешанным начальным моментом порядка 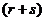называется математическое ожидание произведения 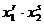, т. е.

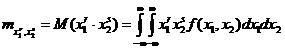, где символ M(z) означает интегрирование с весом 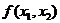выражения, стоящего в скобках.

Если в (1.1.) r=1, s=0, то 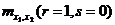равняется математическому ожиданию

.

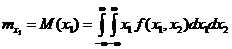Для двумерного вектора определен также центральный смешанный момент

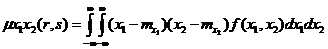. (1.2)

Для случайных величин 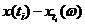определим аналогично одномерные начальные и центральные моменты. Введем следующие определения.

Определение 1.3.

Величина

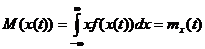(1.3)

называется математическим ожиданием случайной функции. Она является уже не случайной функцией аргумента t.

Величина

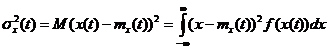(1.4) называется дисперсией случайной функции. Как и математическое ожидание, 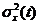представляет собой неслучайную функцию аргумента t.

С помощью формулы (1.2) определим для случайных величин 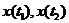смешанный, центральный момент второго порядка.

Определение 1.4.

Неслучайная функция двух аргументов

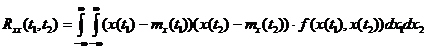(1.5)

называется корреляционной функцией.

Есл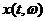и и 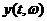- две случайные функции, то для них аналогично (1.5) определена взаимная корреляционная функция

.

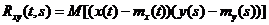Более подробно корреляционные функции будут рассмотрены в разд. 4.