Общие свойства случайных фнкций и случайных

ВЕРОЯТНОСТНЫЕ ПРОЦЕССЫ

В АСУ

Учебное пособие

по дисциплине Теория вероятностей, математическая статистика и случайные процессы.

для студентов специальности 22020 « Автоматизированные системы обработки информации и управления»

Москва 2005

А Н Н О Т А Ц И Я

В учебном пособии рассматриваются общие свойства случайных функций и случайных процессов. Изучаются дискретные Марковские процессы и цепи, характерные для задач анализа и синтеза АСУ. Изучаются пуассоновские процессы в системах массового обслуживания. Определяются линейные операции над случайными процессыми с непрерывным временем.

Описываются методы представления случайных процессов на конечном интервале времени в виде ряда Корунена – Лоэва.

Учебное пособие предназначено для студентов

Специальности 0646.

Ил. 6, табл. I, список лит. – 7 назв.

ВВЕДЕНИЕ

Современные автоматизированные системы управления характеризуются большим количеством взаимосвязанных и взаимодействующих элементов, иерархической структурой, наличием интенсивных потоков информации, сложностью выполняемых функций для достижения целей функционирования. Функционирование реальной автоматизированной системы сопряжено с воздействием большого числа случайных факторов, среди которых можно выделить, например, ошибки измерительных приборов в АСУТП, выходы из строя отдельных элементов и узлов, сбои вычислительных устройств, задержки или искажения при передаче информации от внешних источников, случайных колебаний интенсивности потоков заданий пользователей АСУ и др. Случайные воздействия, как правило, приводят к отклонениям от нормальных режимов функционирования и снижают эффективность и качество работы автоматизированной системы управления. Поэтому в задачах анализа и синтеза АСУ учет влияния случайных факторов играет большую роль.

В общем случае процесс управления включает в себя получение исходной информации о системе и окружающей среде, прогнозирование поведения системы в зависимости от различных условий функционирования, наконец, выбор управляющего воздействия, обеспечивающего оптимальное поведение системы. Из-за воздействия случайных факторов прогноз поведения системы носит вероятностный характер и описывается совместными законами распределения вектора состояний системы. Следовательно, для выработки управляющего воздействия необходимо владеть вероятностными методами описания и исследования поведения сложных систем.

В настоящее время вероятностные методы исследования сложных систем получили существенное развитие и широко применяются инженерами при решении разнообразных задач анализа и синтеза сложных систем. Именно поэтому в учебном пособии рассмотрены лишь методы, получившие наиболее широкое применение в практике решения инженерных задач в АСУ.

В I части учебного пособия описываются общие свойства случайных функций и случайных процессов. Изучаются марковские процессы и цепи. Рассматриваются пуассоновские процессы. Изучаются вопросы представления случайных процессов на конечном интервале времени.

II часть учебного пособия будет посвящена задачам оптимальной фильтрации и прогнозирования стационарных, случайных процессов.

В III части будут рассмотрены вопросы статического анализа случайных процессов и временных рядов. Учебное пособие предполагает знание основ теории вероятностей в объеме учебной программы по «Высшей математике» для студентов специальности 0646, что соответствует первым трем частям учебного пособия [1].

ОБЩИЕ СВОЙСТВА СЛУЧАЙНЫХ ФНКЦИЙ И СЛУЧАЙНЫХ

ПРОЦЕСОВ

1.1 Определение случайных функций

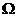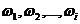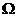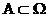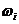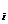При изучении случайных величин удобным приемом, облегчающим анализ, является введение некоторого абстрактного множества с элементами . Само множество называется пространством элементарных событий, а некоторые его подмножества - событиями. Каждому элементарному событию соответствует выборочное значение случайной величины x . 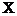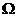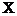Саму случайную величину нужно рассматривать теперь как некоторую функцию, отображающую точки в [1].

Каждому подмножеству 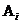из 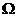ставится в соответствии некоторое число 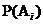, называемое вероятностью события 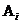и определяются правила (аксиомы) действий с событиями и вероятностями. Такой подход к изучению случайных величин обладает большой общностью и позволяет рассматривать различные типы случайных явлений с единых позиций

При анализе случайных функций, развивая подобный подход, можно считать, что итогом опыта является выборочная функция, определенная на множестве значений 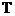некоторого аргумента (параметра) t. Такая математическая модель случайной функции может быть проиллюстрирована, как это показано на рис. 1. на рисунке видно, что каждая точка в выборочном пространстве 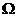отображается в функцию аргумента t. Очевидно, что случайную функцию при данной трактовке можно рассматривать как функцию двух аргументов 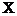(t, ).

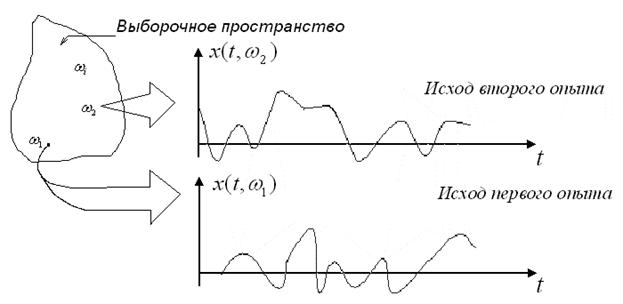
Рис. 1. Выборочное пространство

Преимущество такой трактовки случайных функции - рассматривая различные виды множеств 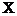, , 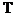, 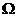можно получать случайные функции различной природы. В наиболее распространенном случае параметр t интерпретируется как время, а множество 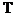составляет отрезок вещественной оси или всю вещественную ось. Если при этом 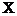является осью действительных чисел, случайная функция 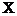(t, ) называется случайным процессом с непрерывным временем.

В качестве определения случайной функции можно взять следующее:

Определение 1.1.

Случайной функцией 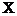(t, ) называется функция двух аргументов

t 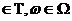со значениями из множества .

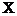Из определения случайной функции следует, что для фиксированного t

функция 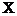(t, 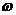) есть случайная величина 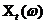с выборочными значениями 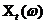, а для фиксированного 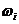- это функция 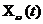аргумента t , которая называется реализацией (выборочной функцией, траекторией). Набор функций 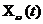, связанных с точками в пространства 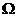, называется ансамблем.

Так как при каждом фиксированном 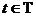значение случайной функции 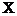(t, 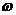) является обычной случайной величиной, то полной характеристикой этого значения является закон распределения 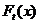. Этот закон распределения зависит, разумеется, от значений параметра t и не зависит от 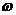. Он характеризует ансамбль при фиксированном t. Знание распределения вероятностей 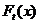является достаточным лишь для самых простейших задач, анализа случайных функций и не позволяет изучать ансамбль функций при любых значениях аргумента t. Для решения задач, в которых необходимо рассматривать значения 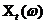при разных t, необходимо рассматривать совместный закон распределения случайных величин .

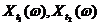Определение 1.2.

Семейство всех совместных распределений для n=1,2,… и всех возможных наборов значений 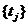называется семейством конечномерных распределений случайного процесса.

Семейство конечномерных распределений является одним из основных понятий теории случайных функций и в значительной степени определяет многие существенные их свойства.

К сожалению, имеются значительные практические трудности в реальном использовании этих семейств для конкретных случайных функций. Существует два общепринятых способа преодоления этих трудностей. Суть первого способа – рассмотрение только тех процессов, в которых любая плотность вероятности n-го порядка имеет определенную структуру может быть получена на основе плотностей вероятностей низшего порядка.

Второй способ заключается в преднамеренном ограничении допустимых операций над случайными функциями, которые могут быть изучены без фактически полного представления (задания) случайной функции. Для таких операций достаточно лишь частичное задание случайной функции. В данном случае вместо многомерных законов распределений ограничиваются рассмотрением соответствующих числовых параметров этих законов.

В качестве числовых параметров конечномерных распределений можно выбирать различные величины, однако наиболее удобными являются начальные и центральные моменты различных порядков. Напомним на примере двумерного случайного вектора 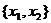с плотностью вероятности 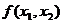, что смешанным начальным моментом порядка 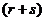называется математическое ожидание произведения 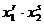, т. е.

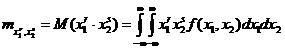, где символ M(z) означает интегрирование с весом 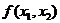выражения, стоящего в скобках.

Если в (1.1.) r=1, s=0, то 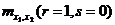равняется математическому ожиданию

.

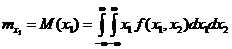Для двумерного вектора определен также центральный смешанный момент

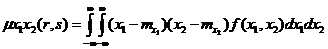. (1.2)

Для случайных величин 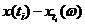определим аналогично одномерные начальные и центральные моменты. Введем следующие определения.

Определение 1.3.

Величина

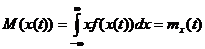(1.3)

называется математическим ожиданием случайной функции. Она является уже не случайной функцией аргумента t.

Величина

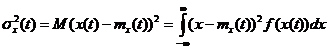(1.4) называется дисперсией случайной функции. Как и математическое ожидание, 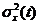представляет собой неслучайную функцию аргумента t.

С помощью формулы (1.2) определим для случайных величин 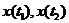смешанный, центральный момент второго порядка.

Определение 1.4.

Неслучайная функция двух аргументов

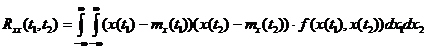(1.5)

называется корреляционной функцией.

Есл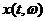и и 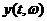- две случайные функции, то для них аналогично (1.5) определена взаимная корреляционная функция

.

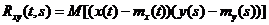Более подробно корреляционные функции будут рассмотрены в разд. 4.

Стационарные процессы

Определение 1.5.

Случайный процесс 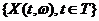называется стационарным, если совместное распределение случайных величин 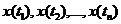совпадает с распределением случайных величин 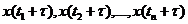для всех 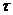, таких, что 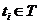и .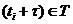

Если равны только первые и вторые моменты распределения, то процесс называется стационарным в широком смысле слова, или слабостационарным процессом.

Случайный процесс с ограниченной дисперсией называется случайным процессом второго порядка.

Нормальные процессы

Случайный процесс называется нормальным или гауссовым, если совместное распределение случайных величин 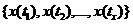является нормальным для каждого n и любых 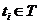, i=1,2,…,R. Нормальные процессы с дискретными аргументами t полностью определяются:

средними значениями

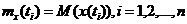
и корреляциями

.

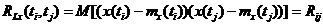Если вести вектор 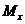и матрицу К

,

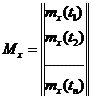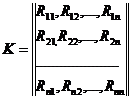
и допустить, что К - невырожденная матрица, что совместное распределение 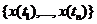можно описать плотностью вероятности

,

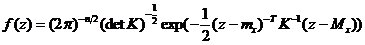где z - n-мерный вектор;

det - детерминант матрицы К;

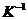- обратная матрица [2].

Каждое совместное распределение такого случайного процесса полностью определяется, таким образом, вектором средних значений 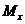и матрицей коэффициентов корреляции К.

Определение 1.6.

Стационарный случайный процесс 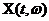называется эргодическим случайным процессом, если для любой функции g(x) от случайной величины x(t) соотношение

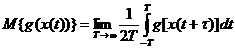(1.7)

выполняется для всех выборочных реализаций, за возможным исключением множества реализаций нулевой вероятности [2].

Последнее добавление в определении эргодического свойства нужно понимать в том смысле, что могут существовать исключительные реализации, для которых средние по времени, найденные по таким реализациям, не могут дать типичных для всего ансамбля результатов. Однако, если вероятность случайного выбора такой исключительной реализации равна нулю, то существование указанных реализаций практически можно не принимать во внимание. Наиболее часто эргодическое свойство случайного процесса используется для определения моментов распределений.

Для эргодических случайных процессов наряду с формулами (1.3) – (1.5) справедливы формулы соответствующих моментов, полученных по одной реализации:

Математического ожидания случайного процесса

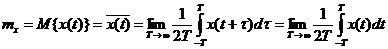; (1.8)

дисперсии случайного процесса

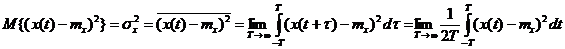; (1.9)

корреляционной функции

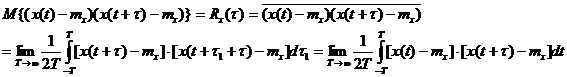(1.10)

В этих соответствиях прямая черта сверху означает операцию усреднения по времени. Явное определение этой операции для каждого из рассмотренных случаев приводится слева от помещенного выражения. В каждом их соотношений при выводе использовано то обстоятельство, что предел интеграла

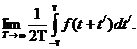
можно записать в виде

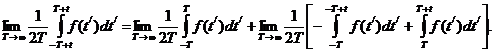
Последний член этого выражения в пределе стремится к нулю и поэтому может быть отброшен.

Соотношения (1.8)-(1.10) удобны для вычислений, так как при условиях, когда эргодическая гипотеза может быть обоснованно принята, они позволяют для оценивания соответствующих характеристик использовать одну выборочную реализацию [2].

Определение 1.7.

Случайный процесс 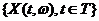называется сингулярным (линейно-сингулярным), если существует случайный оператор L такой, что вероятность

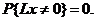
Простым примером сингулярного процесса является процесс

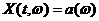для всех t, где a-случайная переменная.

Более сложным примером является процесс

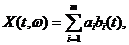
где 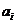-случайные переменные, а 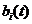-известные неслучайные функции времени.

Сингулярные процессы широко используются в задачах имитационного моделирования вероятностных систем, где с помощью их приближаются реальные процессы.

Определение 1.8.

Случайный процесс 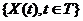называется процессом с независимыми или ортогональными приращениями, если случайные величины

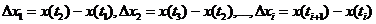взаимно независимы.

Процесс с независимыми приращениями определяется распределением случайной величины 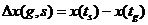для произвольных s, g и распределением 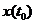. Если распределение 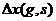зависит только от (s-g),то 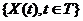называется процессом со стационарными приращениями. Если имеет нормальное распределение, то называется процессом с независимыми нормальными приращениями.

Особенно интересным является винеровский процесс, или процесс броуновского движения [2]. Он имеет большое значение для разработки теории случайных процессов. Типичная выборочная функция этого процесса представлена на рис.2.

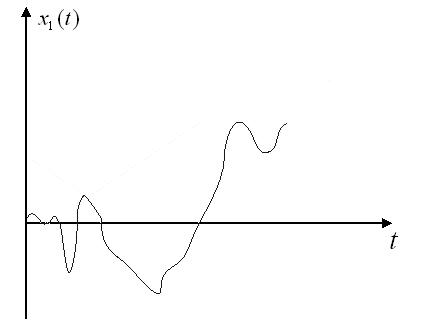
Рис. 2. Выборочная функция винеровского процесса

Винеровский процесс определен для и обладает следующими свойствами:

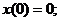
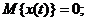
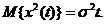(1.11)

Плотность вероятности x(t) имеет вид

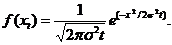
Поскольку винеровский процесс нормальный, он характеризуется полностью математическим ожиданием и корреляционной функцией, имеющих следующий вид:

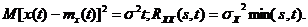
Марковские процессы

Определение 1.9.

Случайный процесс 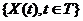называется Марковским процессом, если условные вероятности удовлетворяют равенству

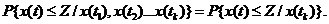(1.12)

Равенство (1.12) означает, что для прогнозирования значения 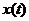нет необходимости знать всю предысторию процесса. Достаточно знать лишь значение .

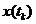Функция распределения величины 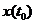называется начальной функцией распределения. Функция

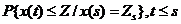(1.13)

называется функцией распределения вероятностей перехода.

Пусть 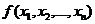- плотность вероятности случайных величин 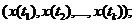используя свойство (1.12), её можно записать в виде

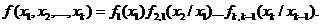(1.14)

применяя формулу полной вероятноcти [1], выражение (1.14) можно привести к виду

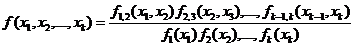(1.15)

Если 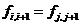, то Марковский процесс полностью определяется двумя функциями: функцией распределения и вероятностью перехода (1.12).

Марковские случайные процессы, особенно с дискретными значениями 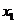, являются исключительно важными для вероятностных задач анализа и синтеза АСУ. Они подробно будут рассмотрены в раз. 2.

Примеры дискретных случайных процессов

Исключительно важную роль в задачах анализа и синтеза автоматизированных систем управления играют дискретные случайные процессы.

Дело в том, что в большинстве случаев процесс функционирования АСУ и ее элементов удобно представлять как последовательность выполнения некоторого набора действий (операций по подготовке данных и вводу, выполнение программ, передача данных и т.д.). Эти процессы рассматриваются во времени и одной из основных задач анализа и синтеза АСУ является исследование их временных характеристик, таких, как интервалы времени простоя устройств, времени выполнения программ, изменение производительности вычислительных систем и т. п. Для реальных АСУ типично наличие элементов случайности при инициировании запросов пользователей, в состоянии компонентов комплекс технических средств АСУ, в длительности выполнения программ, связанных с поиском и сортировкой, и т. д. Все эти обстоятельства вынуждают рассматривать процесс функционирования комплекса технических средств АСУ как случайный.

Пример 1. Простейшей моделью вычислительной системы пакетной обработки является модель [ 4 ].

Прочитанные перфокарты с заданиями через буфер ввода оперативной памяти записываются на магнитный диск, где ожидают очереди на выполнение. Выполнение задания (точнее – результаты выполнения заданий) выводятся на магнитный диск и затем через буфер вывода – на печатающее устройство.

В данной системе возможно возникновение очередей: в устройстве ввода с перфокарт, входных заданий на магнитном диске, выходных заданий на магнитном диске.

Предположим, что число заданий, поступающих в течение n – го периода, является случайной величиной, функция распределения которой не зависит от номера периода и имеет вид

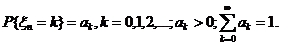(2.1.)

Предположим, что случайные величины 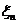независимы. Состояние системы в n – й момент времени определяется как число заданий, ждущих обслуживания к началу n – го периода. Если система находится в состоянии ???, то по прошествии одного периода она перейдет в состояние

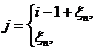если: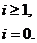

при условии, что за период будет выполнено ровно одно задание.

Очевидно, что если в среднем число заданий, поступающих во вводную очередь на МД, будет превышать число заданий, выводимых из ОП, очередь будет неограниченно возрастать. Очевидно также, что состояние вычислительной системы характеризуются числом 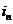и вероятностью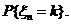

Пример 2. Этот пример связан с задачами управления запасами и снабжением, решаемых в АСУП.

Рассмотрим систему, в которую поступает некоторый товар или некоторое сырье, с целью постоянного удовлетворения спроса. Предположим, что пополнение запаса осуществляется в моменты времени t₁, t₂, ….., а суммарный спрос 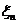на товар в интервале времени 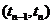представляет собой случайную величину с распределением

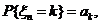к=0, 1, 2, …,

одинаковым для всех интервалов, причем 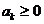и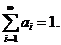

Уровень запаса фиксируется в начале каждого периода. Стратегия пополнения запаса такова: если имеющееся количество товара не превышает некоторого критического уровня s*, то производится немедленное пополнение запаса до уровня s > s*. Если же имеющееся количество товара больше s*, то пополнение не производится. Пусть x _n обозначает уровень запаса непосредственно перед моментом t _n. Пространство состояний процесса {x _n } складывается из возможных значений уровня запаса { x _n , x _n+1, x _n+2, …}.

Согласно описанному правилу уровня запаса двух последовательных периодов связаны соотношениями:

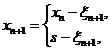если: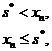

где 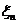– суммарный спрос за n – й период. Если предположить, что случайные величины 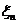независимы, то уровни запаса 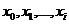образуют марковский процесс с дискретными состояниями.

Цепи Маркова

В примере 2 мы встретились с марковским процессом, пространство состояний которого является дискретным. Рассмотрим такие процессы подробнее.

Определение 2.1.

Марковский случайный процесс 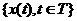называется марковской цепью {x _n}, если множество значений X является конечным или счетным, а аргумент T принимает значения { 0 , ±1_, ±2, …, ± n }.

Пространство состояний процесса удобно отождествлять с множеством неотрицательных целых чисел ( 0, 1, 2, …) и считать, что 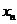находится в состоянии i , если .

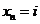Вероятность случайной величины x _n+1 оказаться в состоянии j , если известно, что 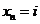обозначается формулой

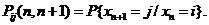
Эта вероятность называется переходной вероятностью за один шаг.

Если переходные вероятности 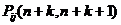не зависят от k = 0, ±1, ±2 … , то говорят, что марковский процесс обладает стационарными переходными вероятностями.

Пользуясь дискретностью множества Х и независимостью 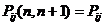от времени, можно записать в виде квадратной матрицы вероятности переходов

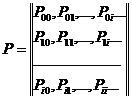
Определение 2.2

Матрица Р называется матрицей переходных вероятностей марковской цепи. Каждая строка этой матрицы представляет собой условное распределение случайной величины x _n+1 при условии, что 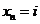, !!= 0, 1, 2,…. .

Очевидно, что элементы и строки матрицы обладают свойствами

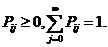
Обычно в вероятностных задачах анализа АСУ множество значений Х конечно и тогда матрица Р – конечная квадратная матрица.

Для стационарной марковской цепи выборочная траектория {x _n } представляет собой последовательность номеров ( или каких либо символов ), соответствующих состояниям, в которых процесс находится в моменты времени n = 1, 2, .….

Как правило, марковскую цепь рассматривают, начиная с некоторого момента времени t, причем полагая : t = 0. Обозначим 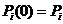- безусловную вероятность того, что в момент времени n = 0 процесс находится в состоянии 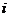. Тогда

Для стационарных марковских процессов справедлива следующая теорема.

Теорема 2.1. Для стационарной марковской цепи вероятность

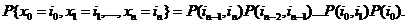(2.2) Для доказательства заметим, что по определению условной вероятности имеем

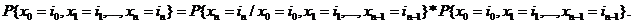
(2.3)

Но по определению марковского процесса

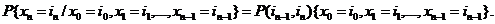(2.4)

Подставляя (2.3) в (2.4), получим :

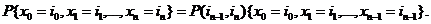
Продолжая по индукции, получим равенство (2.2).

2.2.2. Матрица вероятностей перехода за n шагов.

Одной из важнейших характеристик марковской цепи является матрица переходных вероятностей за n шагов 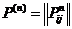, каждый элемент которой обозначает вероятность того, что процесс перейдет из состояния 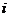в состояние за n шагов.

Независимость поведения от предыстории позволяет выразить вероятность 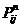через 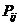, как это видно из следующей теоремы.

Теорема 2.2. Если 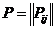- матрица одношаговых переходных вероятностей марковской цепи, то

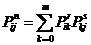(2.5)

Для любой фиксированной пары неотрицательных чисел

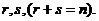
Для доказательства рассмотрим событие, состоящее в переходе из состояния 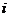в состояние за два шага ( n = 2 ). Это событие может произойти любым из следующих взаимно исключающих друг друга путей: на первом шаге – переход в некоторое промежуточное состояние k (k= 0, 1, 2 ….), затем на втором шаге, переход из состояния k в состояние . Так как процесс марковский, то вероятность второго перехода равна 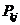, а первого 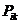. Отсюда в силу формулы полной вероятности получим

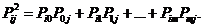
Для случая n > 2, повторяя рассуждения, приходим к такому же выводу. Формуле ( 2.5 ) можно придать рекуррентный вид.

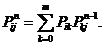
Другой удобной формой для представления 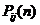является формула

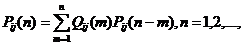(2.6)

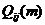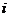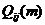где - вероятность перехода из в точно за m шагов ( т.е. без попадания в до m – го шага). Величина равняется, очевидно,

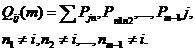(2.7)

Обозначим 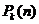- вероятность (полную) оказаться в момент времени n в состоянии с номером K. Тогда, как это видно из (2.5),

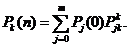(2.8)

Важнейшей задачей анализа марковских цепей является исследование асимптотического поведения вероятностей 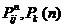при n → .

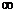Для проведения такого исследования введем классификацию состояний марковских цепей.

2.3. Классификация состояний марковских цепей

Введем следующие определения.

Определение 2.3.

Состояние s_n достижимо из состояния 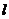, если существует такое n ≥ 0, что

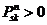, т.е. если вероятность попасть из состояния в состояние K – неотрицательное.

Определение 2.4.

Множество состояний С называется замкнутым, если любое состояние вне С не может быть достигнуто из С.

Определение 2.5.

Цепь называется неприводимой, если в ней нет никаких замкнутых множеств, кроме множества всех состояний, или, иными словами: цепь является неприводимой тогда и только тогда, когда любое ее состояние может быть достигнуто из любого другого состояния.

Рассмотрим теперь произвольное, но фиксированное состояние и предположим, что в момент О система находится в . Всякий раз, когда система возвращается в состояние , восстанавливается первоначальное положение. Время возвращения 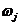является, очевидно, случайной величиной. Каждое состояние характеризуется своим распределением времени первого возвращения { }.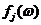

Величины 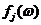можно вычислить, зная 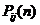и используя следующие соотношения:

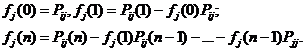(2.9)

Сумма 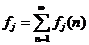представляет собой вероятность того, что, исходя из , система когда-нибудь вернется в .

Определение 2.6.

Состояние называется возвратимым, если 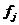= 1. Среднее время возвращения равно

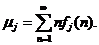
Состояние называется нулевым состоянием, если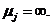

Если в начальный момент система находится в состоянии 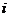, то время ожидания первого достижения имеет распределение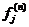

где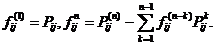

Состояние 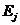невозвратимо, если 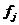<1. В случае если 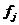= 1, но среднее время возвращения 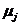бесконечно, состояние называется возвратным нулевым состоянием.

Определение 2.7.

Состояние называется периодическим с периодом t > 1, если 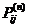= 0 для любого n некратного t и t - наименьшее целое число, обладающее этим свойством.