Обязательный минимум содержания
СОДЕРЖАНИЕ
| Стр. | |
| Введение 1. История развития начального математического образования в России с 1918 года по настоящее время 2. Федеральный компонент государственного стандарта: начальная школа (математика) 3. Современные программы математического образования младших школьников 3.1. Содержательно – методическая характеристика математического блока программы "Школа России" 3.2. Содержательно – методическая характеристика математического блока программы "Гармония" 3.3. Содержательно – методическая характеристика математического блока программы "Школа 2000…" 3.4. Содержательно – методическая характеристика математического блока программы "Школа 2100" 3.5. Содержательно – методическая характеристика математического блока программы "Начальная школа XXI века" 3.6. Содержательно – методическая характеристика математического блока программы "Перспективная начальная школа" 3.7. Содержательно – методическая характеристика математического блока развивающей системы Л.В. Занкова 3.8. Содержательно – методическая характеристика математического блока системы обучения Д.Б.Эльконина – В.В. Давыдова Список литературы |
ВВЕДЕНИЕ
Математика сегодня – это одна из жизненно важных областей знания современного человечества, необходимая для существования в цивилизованном обществе. Широкое использование техники, в том числе и компьютерной, требует от индивида определенного минимума математических знаний и представлений.
Существуют различные взгляды на объем и качество этого необходимого для социализации минимума. Проблема создания оптимального курса математики для общеобразовательной школы до сих пор остается актуальной.
На сегодняшний день существует более 15 программ по математике для начальных классов. Что в них общего? Чем они отличаются? Какую из них выбрать? На эти и некоторые другие вопросы помогут найти ответы данные методические рекомендации, состоящие из введения, трех глав, списка литературы.
В первой главе представлен краткий обзор истории развития начального математического образования в России с 1918 года по настоящее время, раскрываются понятия "традиционная" и "альтернативная" системы обучения.
Во второй главе приводится фрагмент Федерального компонента государственного стандарта: начальная школа (математика). Описываются цели изучения математики в начальной школе, обязательный минимум содержания основных образовательных программ, требования к уровню подготовки оканчивающих начальную школу.
В третьей главе дается содержательно – методическая характеристика математических блоков наиболее распространенных в Омском регионе программ для младших школьников, среди которых "Школа России", "Гармония", "Школа 2000…", "Школа 2100", "Начальная школа XXI века", "Перспективная начальная школа", развивающей системы Л.В. Занкова, системы обучения Д.Б. Эльконина – В.В. Давыдова.
Пособие адресовано студентам факультетов педагогики и психологии детства педагогических вузов, учителям начальных классов, родителям младших школьников, преподавателям и слушателям факультетов повышения квалификации работников образования.
1. Этапы математического образования в России с 1918 года по настоящее время
Этап: 1918 – 1931 гг.
В начале революции была проведена большая организационная работа по перестройке школы на основе общих положений о единой трудовой школе. Математика (как и другие учебные дисциплины) в комплексной системе утратила значение самостоятельного учебного предмета и выполняла служебную роль в процессе общественно-политического воспитания молодежи.
Этап: 1931 – 1968 гг.
В 1931 г. ЦК ВКП (б) издал постановление "О начальной и средней школе", в котором, отмечалось, что "…обучение по комплексной системе не дает достаточного объема общеобразовательных знаний и неудовлетворительно решает задачу подготовки для техникумов и высшей школы грамотных людей, хорошо владеющих основами наук".
Начался период перехода на предметную систему обучения. Была разработана программа по математике (действовала в течение почти сорока лет), характерной особенностью которой была строгая система расположения учебного материала, обеспечивающая постепенное нарастание сложности. Вслед за программой появились и стабильные учебники. Основное содержание составлял материал для формирования у детей вычислительных навыков и умений решать арифметические задачи. Сведения теоретического характера (в форме правил и определений) занимали крайне ограниченное место. Только в 1960г. в программу для 4 класса были включены некоторые вопросы теории.
В 50-е годы с особой остротой встал вопрос о связи обучения и развития в процессе преподавания математики. В связи с этим в 60-х годах широко развернулась экспериментально-исследовательская работа (Л.В.Занков, В.В Давыдов, Д.Б. Эльконин и др.).
Разработан проект новой программы по математике для 1-3 классов (Н.А. Менчинская, М.И. Моро, М.А. Бантова, А.С. Пчелко, А.М. Пышкало), которая была подвергнута длительной опытной проверке.
Этап: 1969 – 1983 гг.
1969 г. проект вышеуказанной программы был утвержден Министерством просвещения РСФСР в качестве стабильного начального курса.
С начала 80-х годов начались исследования в области возможного обучения детей 6 - летнего возраста.
В 1983г. программа претерпела некоторые изменения: часть геометрического и алгебраического материала была изъята с целью увеличения внимания формированию вычислительных навыков.
4 этап: с 1983 до настоящего времени.
С 1986 года началось одновременное обучение детей и 6 и 7 лет. Были созданы новые программы и учебники для 6-ти летних.
В 1993 года началась массовая экспериментальная апробация систем Эльконина – Давыдова и Занкова. С 1996 года обе системы обучения были внедрены в практику работы школы как вариативные.
В настоящее время для младших школьников существует более 15 программ по математике. Перечислим наиболее распространенные из них (табл. 1):
Таблица 1
| № | Система обучения | Название программы | Авторские коллективы |
| 1. | "Школа России" | Математика | М.И. Моро, Ю.М. Колягин, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова, С.В. Степанова |
| 2. | "Гармония" | Математика | Н.Б. Истомина, И.Б. Нефедова |
| 3. | "Школа 2000…" | Математика | Л.Г. Петерсон |
| 4. | "Школа 2100" | Моя математика | Т.Е. Демидова, С.А. Козлова, А.П. Тонких |
| 5. | "Начальная школа XXI века" | Математика | В.Н. Рудницкая, Т.В. Юдачева |
| 6. | "Перспективная начальная школа" | Математика | А.Л. Чекин, Е.П. Юдина, Н.К. Булычева |
| 7. | Система обучения Л.В. Занкова | Математика | И.И. Аргинская, Е.И. Ивановская, Е.П. Бененсон, Л.С. Итина |
| 8. | Система обучения Д.Б.Эльконина – В.В. Давыдова | Математика | Э.И. Александрова |
Следует отметить, что вышеуказанные программы относятся как к традиционной, так и альтернативным системам обучения.
Зачастую "традиционной" называют программу "Школа России". Это связано с тем, что в течение длительного времени (с 1968 года) она была единственной для обучения математике в начальной школе. "Альтернативными" в 90-х годах XX века стали называть опубликованные учебники других авторов, среди которых были книги Н.Б. Истоминой, Л.Г. Петерсон, И.И. Аргинской и др.
В то же время, следует отметить, что подобная классификация не является истинной. Как отмечает А.М. Пышкало, традиционный курс математики для начальных классов характеризуется определенной последовательностью изучаемых базисных понятий (рис. 1):
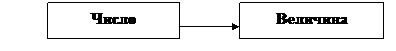
Рис. 1
Данная последовательность характерна не только для программы М.И. Моро, М.А. Бантовой и др., но и Н.Б. Истоминой; С.И. Волковой, Н.Н. Столяровой «Развитие познавательных способностей учащихся на уроках математики»; С.И. Волковой, О.Л. Пчелкиной «Математика и конструирование»; И.И. Аргинской; П.М. Эрдниева.
Альтернативными в таком случае называются системы, в которых принят другой порядок изучения математических понятий (рис. 2, 3, 4):
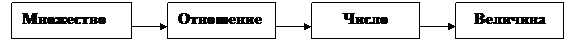
1)
Рис. 2
Программы К.И. Нешкова, Ю.Н. Макарычева, А.М. Пышкало; В.Н. Рудницкой; А.И. Маркушевича; Н.Г. Салминой, В.А. Тарасова.
2) 
Рис. 3
Программа: Л.Г. Петерсон.
|
|

Рис. 4
Программы по системе обучения Д.Б. Эльконина – В.В. Давыдова; Л.М. Фридмана.
Несмотря на различия в подходах изучения материала, содержание всех программ по математике должно соответствовать обязательному минимуму содержания образования государственного стандарта (Приказ Минобразования России от 05.03.2004г. № 1089).
2. Федеральный компонент государственного стандарта: начальная школа (математика)
Изучение математики на ступени начального общего образования направлено на достижение следующих целей:
· развитиеобразного и логического мышления, воображения; формирование предметных умений и навыков, необходимых для успешного решения учебных и практических задач, продолжения образования;
· освоениеоснов математических знаний, формирование первоначальных представлений о математике;
· воспитаниеинтереса к математике, стремления использовать математические знания в повседневной жизни.
Числа и вычисления
Счет предметов. Название, последовательность и запись чисел от 0 до 1000000. Классы и разряды. Отношения «равно», «больше», «меньше» для чисел, их запись с помощью знаков =, <,>.
Сложение и вычитание чисел, использование соответствующих терминов. Таблица сложения. Отношения «больше на…», «меньше на…».
Умножение и деление чисел, использование соответствующих терминов. Таблица умножения. Отношения «больше в…», «меньше в…». Деление с остатком.
Арифметические действия с нулем.
Определение порядка выполнения действий в числовых выражениях. Нахождение значений числовых выражений со скобками и без них.
Перестановка слагаемых в сумме. Перестановка множителей в произведении. Группировка слагаемых в сумме. Группировка множителей в произведении. Умножение суммы на число и числа на сумму. Деление суммы на число.
Устные и письменные вычисления с натуральными числами. Использование свойств арифметических действий при выполнении вычислений. Нахождение неизвестного компонента арифметических действий. Способы проверки правильности вычислений.
Сравнение и упорядочение объектов по разным признакам: длине, массе, вместимости. Единицы длины (миллиметр, сантиметр, дециметр, метр, километр), массы (грамм, килограмм, центнер, тонна), вместимости (литр), времени (секунда, минута, час, сутки, неделя, месяц, год, век).
Установление зависимостей между величинами, характеризующими процессы: движения (пройденный путь, время, скорость); работы (объем всей работы, время, производительность труда); «купли-продажи» (количество товара, его цена и стоимость). Построение простейших логических выражений типа "…и/или…", "если…, то…", "не только, но и…".
Решение текстовых задач арифметическим способом (с опорой на схемы, таблицы, краткие записи и другие модели).
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ
Знать / понимать
· последовательность чисел в пределах 100000;
· таблицу сложения и вычитания однозначных чисел;
· таблицу умножения и деления однозначных чисел;
· правила порядка выполнения действий в числовых выражениях;
Уметь
· читать, записывать и сравнивать числа в пределах 1000000;
· представлять многозначное число в виде суммы разрядных слагаемых;
· пользоваться изученной математической терминологией;
· выполнять устно арифметические действия над числами в пределах 100 и с большими числами в случаях, легко сводимых к действиям в пределах 100;
· выполнять деление с остатком в пределах 100;
· выполнять письменные вычисления (сложение и вычитание многозначных чисел, умножение и деление многозначных чисел на однозначное и двузначное число);
· выполнять вычисления с нулем;
· вычислять значение числового выражения, содержащего 2-3 действия (со скобками и без них);
· проверять правильность выполненных вычислений;
· решать текстовые задачи арифметическим способом (не более 2 действий);
· чертить с помощью линейки отрезок заданной длины, измерять длину заданного отрезка;
· распознавать изученные геометрические фигуры и изображать их на бумаге с разлиновкой в клетку (с помощью линейки и от руки);
· вычислять периметр и площадь прямоугольника (квадрата);
· сравнивать величины по их числовым значениям, выражать данные величины в различных единицах;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
· ориентировки в окружающем пространстве (планирование маршрута, выбор пути передвижения и др.);
· сравнения и упорядочения объектов по разным признакам: длине, площади, массе, вместимости;
· определения времени по часам (в часах и минутах);
· решения задач, связанных с бытовыми жизненными ситуациями (покупка, измерение, взвешивание и др.);
· оценки размеров предметов;
· самостоятельной конструкторской деятельности (с учетом возможностей применения разных геометрических фигур).
3. Современные программы математического образования младших школьников
Современное начальное математическое образование является частью системы среднего образования и в то же время своеобразной самостоятельной ступенью обучения. Новое содержание математического образования ориентировано на формирование культуры и самостоятельности мышления младших школьников, элементов учебной деятельности средствами и методами математики. В ходе обучения дети должны овладеть общими способами действий, осуществляя пошаговый контроль и самооценку выполненной деятельности с целью установления соответствия своих действий намеченному плану.
В последние годы в связи с изменением целей начального образования и вытекающим из этого обновлением содержания и методов преподавания всех образовательных областей появилась вариативность на уровне образовательных систем и учебных курсов. Учителям начальной школы предлагается ряд обновленных программ по математике, оснащенных учебно-методическими комплектами. Приказом Минобразования России от 05.03.2004г. № 1089 утвержден обязательный минимум содержания начального общего образования (стандарт), в котором в числе других определено содержание образовательной области "Математика". Авторы всех вариативных программ для начальной школы обеспечивают выполнение обязательного минимума содержания, расширяя и углубляя его.
В четырехлетней начальной школе на изучение образовательной области "Математика" в Базисном учебном плане общеобразовательных учреждений Российской Федерации (приказ Минобразования России от 09.03.2004г. №1312) в инвариантной (обязательной) части во всех классах выделено по 4 часа в неделю.
Во всех разработанных для младших школьников программах по математике учтены возрастные особенности и возможности детей (наглядно-действенный характер мышления, непроизвольность внимания, эмоциональность и т.п.). В учебно-методических комплектах широко используются дидактические и сюжетно-ролевые игры, практические упражнения, занимательные задания и т.д. При изложении учебного материала учитываются принцип наглядности и практическая направленность обучения.
3.1. Содержательно – методическая характеристика математического блока программы "Школа России"
Авторы:М.И. Моро, Ю.М. Колягин, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова, С.В. Степанова.
Особенности программы
Данный начальный курс математики интегрированный: в нем объедены арифметический, алгебраический и геометрический материал. Основу составляют представления о натуральном числе и нуле, четырех арифметических действиях с целыми неотрицательными числами и важнейших их свойствах, а также основанное на этих знаниях осознанное и прочное усвоение приемов устных и письменных вычислений. Важное место занимает ознакомление с величинами и их измерением.
Курс построен концентрически, что позволяет соблюсти постепенность в нарастании трудности учебного материала и создает хорошие условия для совершенствования формируемых знаний, умений и навыков.
Ведущие принципы обучения:
· учет возрастных особенностей учащихся;
· органическое сочетание обучения и воспитания;
· усвоение знаний и развитие познавательных способностей;
· практическая направленность преподавания;
· индивидуальный подход к учащимся.
Практическая направленность методики выражена в следующих положениях:
1. Сознательное усвоение детьми различных приемов вычислений обеспечивается за счет использования рационально подобранных средств наглядности и моделирования с их помощью тех операций, которые лежат в основе рассматриваемого приема. Предусмотрен постепенный переход к обоснованию вычислительных приемов на основе изученных теоретических положений (переместительное свойство сложения, связь между сложением и вычитанием, сочетательное свойство сложения и др.).
2. В программе заложен механизм формирования у детей сознательных и прочных навыков устных и письменных вычислений, доведения до автоматизма знания табличных случаев действий. Этому способствует хорошо распределенная во времени, оптимальная насыщенная система упражнений, а также ограничение действий над числами пределами миллиона, отказ от изучения ряда относительно сложных для детей этого возраста вопросов, не имеющих принципиального значения для продолжения математического образования.
3. Алгоритмизация курса выражена в усилении роли алгоритмов при рассмотрении таких вопросов, как письменные вычисления, правила выполнения действий в числовых выражениях, проверка действий и т.п. Введены новые алгоритмы, усовершенствованы традиционные.
4. Рассмотрение теоретических вопросов курса опирается на жизненный опыт ребенка, практические работы, различные средства наглядности, подведение детей на основе собственных наблюдений к индуктивным выводам, сразу же находящим применение в учебной практике.
5. Система упражнений, направленных на выработку навыков, предусматривает их применение в разнообразных условиях. Тренировочные упражнения рационально распределены во времени. Значительно усилено внимание к практическим упражнениям с раздаточным материалом, к использованию схематических рисунков, а также предусмотрена вариативность в приемах выполнения действий, в решении задач.
6. На первых порах обучения важное значение имеет игровая деятельность детей на уроках математики. В программе приведен примерный перечень дидактических игр и игровых упражнений.
Нумерация чисел
Формирование понятия о натуральном числе начинается с первых уроков и проводится на основе практических действий с различными группами предметов. Такой подход дает возможность использовать ранее накопленный детьми опыт, их первоначальные знания о числе и счете. Позволяет с самого начала вести обучение в тесной связи с жизнью.
В 1 классе на примере чисел первого десятка выясняется, как образуется каждое следующее число в натуральном ряду, устанавливается соотношение между любым числом ряда и всеми предшествующими или последующими числами, учащиеся знакомятся с различными способами сравнения чисел (сначала на основе сравнения соответствующих групп предметов, а затем по месту, которое занимают сравниваемые числа в ряду). Младшие школьники должны усвоить названия, последовательность и обозначение чисел от 1до 20. Происходит знакомство с числом 0.Особое внимание уделяется десятичному составу чисел от 11 до 20, чтению и записи чисел второго десятка.
Во 2 классе учащиеся знакомятся с новой счетной единицей – десяток, узнают, что десятками можно считать также как и единицами. Рассматривается образование и название чисел от 1 до 100, их десятичный состав, запись и чтение, сравнение. Вводятся понятия однозначного и двузначного числа.
3 класс. Образование и названия трехзначных чисел. Порядок следования при счете. Запись и чтение трехзначных чисел. Представление трехзначного числа в виде суммы разрядных слагаемых. Сравнение чисел. Увеличение и уменьшение числа в 10, 100 раз.
В 4 классе вводится новая счетная единица – тысяча. Происходит знакомство не только с разрядами, но и классами: класс единиц, класс тысяч, класс миллионов и т.д. Дети учатся читать, записывать, сравнивать многозначные числа, представлять их в виде суммы разрядных слагаемых. Рассматриваются случаи увеличения (уменьшения) числа в 10, 100, 1000 раз. Понятие «числовой луч».
Арифметический материал
Уверенное овладение детьми навыками устных и письменных вычислений является одной из основных задач начального обучения математике, так как это необходимо для продолжения обучения и позволяет решать любую вычислительную задачу без использования специальных средств.
В 1 классе в теме "Десяток" учащиеся должны запомнить таблицу сложения в пределах 10 и соответствующие случаи вычитания, а также случаи сложения и вычитания с числом 0. Рассматриваются приемы вычислений: при сложении – прибавление числа по частям, перестановка чисел; при вычитании – вычитание числа по частям и вычитание на основе знания соответствующего случая сложения.
При изучении второго десятка рассматриваются случаи сложения и вычитания вида 10+7, 17-7, 16-10 (основаны на нумерации), а также сложение двух однозначных чисел, сумма которых больше, чем 10, с использованием изученных приемов вычислений.
Центральной задачей при изучении раздела "Числа от 1 до 100" является изучение табличного сложения и вычитания, умножения и деления.
Внетабличное сложение и вычитание, умножение однозначных чисел и соответствующие случаи деления рассматриваются в теме "Числа от 1 до 100", которая изучается в 3 классе. Причем рассматриваются как устные, так и письменные приемы вычислений.
К окончанию 4 класса учащиеся должны усвоить все предусмотренные программой приемы вычислений (как устные, так и письменные) на множестве многозначных чисел.
Алгебраический материал
При изучении сложения и вычитания в пределах 10 дети знакомятся с названиями действий, их компонентов и результатов, терминами "равенство" и "неравенство". В дальнейшем, во 2 классе, вводятся термины "выражение", "значение выражения". Вместо привычного "решение примеров" в речи учителя и учащихся должно звучать: "Найдем значение выражения", "Сравним выражения" и т.п.
Помимо терминологии дети усваивают и некоторые элементы математической символики: знаки действий (плюс, минус), знаки отношений (больше, меньше, равно); они учатся читать и записывать простейшие математические выражения вида 5+4 (сумма чисел 5 и 4), 7-2 (разность чисел семь и два), а также более сложные выражения вида 6+(6-2).
В программе предусмотрено ознакомление с некоторыми свойствами арифметических действий и основанными на них приемами вычислений. Так в теме "Числа от 1 до 10" дети знакомятся с переместительным свойством суммы, учатся пользоваться приемом перестановки слагаемых в тех случаях, когда его применение облегчает вычисления (2+7, 1+6). На основе практических действий с предметами учащиеся знакомятся с тем, что прибавить или вычесть число можно по частям (6+3=6+2+1, 6-3=6-2-1). Таким образом, они практически знакомятся с сочетательным свойством суммы, которое во 2 классе будет специально рассмотрено и сформулировано.
К элементам алгебраической пропедевтики относится ознакомление детей с таким важным математическим понятием, как понятие переменной. Уже в теме "Числа 1-10", после введения названий компонентов и результатов сложения и вычитания, учащимся предлагаются задания, в которых, например, значения слагаемых заданы в табличной форме и требуется найти суммы и заполнить соответствующие клетки таблицы. В дальнейшем вводится буквенное обозначение переменной. Дети учатся находить значение буквенных выражений при заданных числовых значениях входящих в них букв.
Постепенно, начиная с решения подбором так называемых примеров с окошком вида □+3=7, учащиеся знакомятся с простейшими уравнениями (х·8=56, х+9=19 и т.п.), у них формируется понятие о том, что значит решить уравнение. В теме "Числа от 1 до 100" программой предусмотрено решение уравнений на основе знания взаимосвязей между компонентами и результатами действий. В 4 классе усложняется и структура решаемых уравнений (х·8=246-86). Это способствует формированию у детей понятий "равенство", "левая и правая части равенства".
Введение буквенных выражений используется и при формировании некоторых обобщений. Так, например, в формулах вида: 1·а=а, х·1=х, 0·с=0 и т.п. фиксируются общие положения, важные для понимания смысла действий.
Геометрический материал
Геометрический материал предусмотрен программой для каждого класса.
1 класс: Уточняются пространственные представления младших школьников: вверху, внизу (выше, ниже), слева, справа (левее, правее), перед, за, между, рядом. Идет знакомство с геометрическими фигурами: точка, линии (кривая, прямая, отрезок, ломаная), многоугольник (углы, вершины, стороны многоугольника).
2 класс: Углы прямые и непрямые. Прямоугольник (квадрат). Свойство противоположных сторон прямоугольника. Свойство диагоналей прямоугольника (квадрата).
3 класс: Обозначение геометрических фигур буквами. Круг. Окружность. Центр, радиус, диаметр окружности (круга). Виды треугольников: равносторонни, равнобедренные.
4 класс: Луч. Виды углов: прямой, острый, тупой. Виды треугольников: прямоугольный, остроугольный, тупоугольный.
При формировании представлений о фигурах большое значение придается проведению практических упражнений:
· связанных с построением, учащиеся должны научиться строить на клетчатой и нелинованной бумаге прямой угол, прямоугольник (квадрат) произвольного и заданного размера, строить заданный отрезок;
· вычерчивание и преобразование одних фигур в другие;
· на рассмотрение некоторых свойств изучаемых фигур, например, свойства противоположных сторон прямоугольника, диагоналей прямоугольника и квадрата);
· направленных на развитие геометрической зоркости – умение узнавать геометрические фигуры на сложном чертеже, составлять заданные геометрические фигуры из частей и др.
Работа над геометрическим материалом по возможности увязывается с изучением арифметических вопросов (геометрические фигуры и их элементы используются в качестве объектов счета предметов), величин (нахождение площади и периметра прямоугольника), с процессом формирования представлений о долях величины (отрезки, многоугольники, круг используются в качестве наглядной основы), при решении текстовых задач (схематический чертеж).
Величины и их измерение
При формировании представлений о величинах (длине, массе, площади и др.) учитель опирается на опыт ребенка, уточняет и расширяет его. Так, при ознакомлении с понятием длины сначала используют такие приемы, как сравнение "на глаз", затем прием наложения, на следующем этапе вводятся различные мерки. В ходе выполнения таких заданий учащиеся подводятся к самостоятельному выводу о необходимости введения единых общепринятых единиц измерения каждой величины. Дети знакомятся с измерительными инструментами.
1 класс: В концентре "Десяток" учащиеся знакомятся с длиной отрезка, единицей измерения – сантиметр. Организуется работа по формированию временных представлений: сначала, потом, до, после, раньше, позже. При изучении чисел от 11 до 20 полученные знания закрепляются, вводится новая единица измерения – дециметр. Устанавливаются соотношения между ними. Кроме того, происходит знакомство с часом, дети учатся определять время по часам с точностью до часа. Изучение массы и объема начинается с введения единиц измерения – килограмм и литр.
2 класс: Полученные в 1 классе знания закрепляются и уточняются на новом числовом множестве – числа от 1 до 100. Вводится понятие – длина ломаной. Рассматриваются единицы измерения и соотношения между ними: длины – сантиметр, дециметр, миллиметр; времени – час, минута (определение времени по часам с точностью до минуты).
Кроме того, учащиеся знакомятся с периметром многоугольника.
3 класс: Площадь. Единицы площади: квадратный сантиметр, квадратный дециметр. Соотношение между ними. Площадь прямоугольника (квадрата).
Единицы времени: год, месяц, сутки.
Единица длины – метр. Соотношения метра и миллиметра, сантиметра, дециметра.
Единица массы – грамм. Соотношение грамма и килограмма.
Ознакомление с единицами измерения величин и их соотношениями проводится в течение всех лет обучения в начальной школе.
Одной из основных задач четвертого года обучения становится пополнение и обобщение этих знаний. Необходимо рассмотреть соотношение между единицами каждой величины.
Единицы длины: миллиметр, сантиметр, дециметр, километр.
Единицы площади: квадратный миллиметр, квадратный сантиметр, квадратный дециметр, квадратный метр, квадратный километр, ар, гектар.
Единицы массы: грамм, килограмм, центнер, тонна.
Единицы времени: секунда, минута, час, сутки, месяц, год, век.
Эти соотношения усваиваются учащимися при выполнении различных заданий и разучивании соответствующих таблиц. Программой предусмотрено также изучение приемов сложения и вычитания значений одной и той же величины, а также умножение и деление значений величины на однозначное число.
Дроби и доли
Изучение темы начинается в 3 классе, где учащиеся знакомятся с понятием доли. Учатся их сравнивать с использованием наглядности. Решают задачи на нахождение доли числа и числа по его доле. Полученные знания закрепляются в 4 классе, где учащимся предлагается "Материал для углубления знаний о долях".
Текстовые задачи
Важнейшей особенностью начального курса математики является то, что рассматриваемые в нем основные понятия, отношения, взаимосвязи, закономерности раскрываются на системе соответствующих конкретных и чаще всего сюжетных текстовых задач. Например, решение простых текстовых сюжетных задач (решаемые одним действием) способствует более осознанному усвоению детьми:
· смысла самих действий;
· отношений "больше – меньше" (на сколько единиц и в несколько раз), "столько же";
· взаимосвязи между компонентами и результатами действий»;
· связи между пропорциональными величинами (цена, количество, стоимость; скорость, время, расстояние и т.п.).
При обучении математике важно научить детей самостоятельно находить путь решения предлагаемых программой задач, применять общие подходы к их решению.
Требования программы к умениям учащихся решать задачу:
1. Дети должны уметь анализировать содержание задачи, объясняя:
· что известно и что неизвестно в задаче,
· что можно узнать по данному условию,
· что нужно знать для ответа на вопрос задачи,
· какие арифметические действия и в какой последовательности должны быть выполнены для получения ответа на вопрос задачи.
2. Должны обосновывать выбор каждого действия и пояснять полученные результаты.
3. В 1 классе записывать решение задачи только по действиям, а в дальнейшем составлять по условию задачи выражение.
4. Вычислять значение составленного выражения.
5. Должны уметь устно давать полный ответ на вопрос задачи и проверять правильность ее решения.
Следует отметить, что учащиеся знакомятся не только с понятием "текстовая задача", но и с различными ее видами. Процесс изучения данного материала равномерно распределен в течение всех четырех лет обучения.
1 класс. Понятие "задача". Компоненты задачи: условие, вопрос. Решение задач в 1 действие, раскрывающие конкретный смысл действий сложения и вычитания; на нахождение числа, которое на несколько единиц больше (меньше) данного.
2 класс. Понятия "обратная задача", "задача с недостающими данными". Простые задачи на нахождение неизвестного слагаемого, уменьшаемого, вычитаемого; раскрывающие конкретный смысл умножения и деления. Решение задач в 2 действия на сложение и вычитание, составление выражений. Рассматриваются различные способы решения задач. Использование моделей и схем на этапе поиска плана решения задачи.
3 класс. Решение задач в 1-3 действия на сложение и вычитание, умножение и деление в течение года. Задачи с пропорциональными величинами (цена, количество, стоимость; масса 1 пакета, количество, масса всех пакетов и т.п.).
4 класс. Решение задач в 2-4 действия. Задачи с пропорциональными величинами. Задачи на движение (встречное движение, движение в противоположных направлениях).
В процессе работы над задачами дети упражняются в самостоятельном составлении задач по различным заданиям учителя. Числовой и сюжетный материал для этого берется как из учебника, так и из окружающей жизни. Работе над задачей можно придать творческий характер: если изменить вопрос задачи; изменить ее условие при сохранении вопроса; поставить дополнительный вопрос; снять вопрос, предложив учащимся самим определить, что можно узнать из условия задачи.
Особенности учебника
В учебниках достаточно рационально расположен основной учебный материал: в наиболее выгодные условия поставлены центральные темы курса каждого класса (вводятся в начале и закрепляются в течение всего учебного года). В конце каждого года обучения в ознакомительном плане вводится учебный материал, подготавливающий к усвоению основных вопросов курса следующего класса. Все это помогает детям прочно и сознательно овладевать математическими знаниями, умениями и навыками.
Развитие интереса к предмету реализуется в учебниках через методическую систему, предполагающую доступность курса для каждого ученика. Материал преподносится в занимательной форме, используются дидактические игры. Широко представлены упражнения, носящие комплексный характер, т.е. требующие применения знаний из различных разделов курса. Они стимулируют развитие познавательных способностей учащихся. Дана система разнообразных постепенно усложняющихся упражнений, связанных с решением текстовых задач, содержание которых определяется требованиями программы. Наряду с решением готовых задач предусмотрены творческие задания на самостоятельное составление задач, на преобразование решенной задачи и др.
К концу начального обуч<
