Влияние характера закрепления сжатого стержня на его устойчивость.

Формой потери потери устойчивости сжатого стержня при выводе формулы Эйлера является полуволна синусоиды:

Y=fsin (5) (5)

В тех расчетных случаях когда условия опирания стержня от выше рассмотренного случая по предложению русск. Ученого Ф.С.Ясинского было введено понятие приведенной длины стержня т.е. условной длины приведенной к полуволне синусоиды:

=µ (6)

ln- приведенная длина

е- фактическая

µ- коэф. Приведения

последняя конструкция устойчивее по сравнению с 1 в 16 раз и тогда окончательно форм. Эйлера принимает вид:

Fкр= (7)

ПРЕДЕЛЫ ПРИМЕНИМОСТИ ФОРМУЛЫ ЕЙЛЕРА

Классификация стальных стержней

F= формула позволяет определить величину критических напряжений

σ_кр =

-минимальн радиус инерции поперечн сечения стержня, то

σ_кр =

λ -безразличный параметр, называемый гибкостью стержня, в зависимости от λ стержни подразделяют на 3 класса

I-стержни малой гибкости или жесткие стержни

II-стержни средней гибкости

III-стержни высокой гибкости или гибкие стержни

Формула Эйлера получена на основе диф. ур изогнутой оси стержня, базирующегося на закономерности Гука.

Формула Эйлера применяется только для тех стержней у кот. величина критических напряжений не превышает предела пропорциональности, т.е. только для гибких стержней

σ_кр≤σ_ц

Стержни I-го класса, т.е. жесткие, достигают предельного состояния без проявления потери устойчивости, т.е.они рассчитываются на обычное осевое сжатие, гибкость(пред)<40

σ_кр≤σ_пред =

Устойчивость стержней среднего класса 2- стержни средней гибкости, экспериментально исследовалось независимым швейцарским учен. Гетмаером и Ясинским.

Ими получены следующие закономерности критич.напр. пластич. материалов

a,b,c –параметры, полученные на основе эксперимент. данных.

ПРАКТИЧЕСКИЙ МЕТОД РАСЧЕТА СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ

Условия устойчивости сжатого стержня аналогично условию прочн. при осевом сжатии

σ=

σ= -условие устойчивоси сжатого стержня

коэффициент снижен. доп-х напр-й за счет гибкости стержня, т.е. коэфф. продольного изгиба является табл. величиной и зависит от гибкости стержня и материала.

Усл-е позволяет решать все 3 типа задач

1.Проверочная задача

σ

2.Проектировочная,на подбор сечения сжатого стержня.

A≥ т.к. поперечное сечение отыскав, а зависит от ,а следовательно ти от размера поперечного сечения. Задача решается способом иперации(последов-х приближений)

В начале первого приближения примен 0.5,находим А,определяем σ и если оно существенно отличается от допускаемой величины,второе и т.д. приближения

3.Определение несущей способности сжатой стойки

В формуле Эйлере определим устойчивость парамметров явл-ся величиной Imin

рацион сечение из 2-х швел.

38. Общий метод расчета элементов конструкций при сложном сопротивлении.

Варианты расчета простых статически неопределимых балок

Существует несколько способов расчета простых балок:

1.Сравнение линейных перемещений.

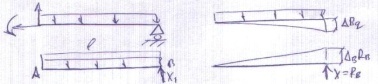
ΔВ=ΔВq+ΔBRB=0(1) доп. уравнение деформаций

Слагаемые в(1) могут быть найдены исп-я готовые таблицы или универсальные уравнения. Применительно к рас-му предмету:

ΔBq=-qe⁴/8EIx; ΔBRB=RBe³ /3EIx;

ΔB=-qe⁴/8EIx +RBe³/3EIx =0 =>RB=3qe/8

2. Сравнение угловых перемещений.

Можно отбросить связь, препятствующая повороту опорного сечения А и записать

ΔA=ΔAq+ΔAMA=0(2)

Также ур-е деформации слагаемое означает углы поворота.

3.Составление замкнутой системы ур-я.

3 ур-я статики+ унивес. ур-е

yB=0.

43. Метод сил для расчета сложных СНС.

Метод при котором за неизвестное принимаются сосредоточенные моменты наз-ся методом сил. Он явл-ся наиболее распространенным и ис-ся для любых упругих систем (балки, рамы,эстакады итд.).

Например: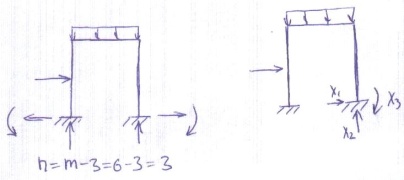

К трем ур-ям статики для решения данной СНС добавится 3 уравнения, выражающие рав-во 0 перемещений по направлениям всех отброшенных связей т.е. опорное сечение и не перемещаются им в горизонтальном или в вертикальном перемещениях и не переворачиваются.

X1 Δ1=0

X2 Δ2=0 (1)

X3 Δ3=0

Каждое уравнение системы(1) можно записать в развернутом виде:

Δ1=Δ11+Δ12+Δ13+Δ1f=0 (2)

Первый символ указывает направление; 2-й воз-е.

Δ1f-перемещение опорного сечения А в направлении действия X, вызванное внешней нагрузкой

(2) можно выразить через единичные перемещения и искомое неизвестное (это первые три слагаемых)

Δ11=δ11-x1 и тогда система примет закончен. вид.

δ11 x1+ δ12 x2+ δ13 x3+ Δ1f=0

δ21 x1+ δ22 x2+ δ23 x3+ Δ2f=0 (3)-система кумс.

δ31 x1+ δ32 x2+ δ33 x3+ Δ3f=0

Канонические ур-я метода сил-КУМС.

Число ур-й равно степени статической неопределимости.