Проверка прочности балок при изгибе по касательным и главным напряжениям.
Проверка по касательным выполняется для опасного сечения балки, где поперечная сила по модулю принимает наибольшую величину. Условие прочности при этом имеет вид:
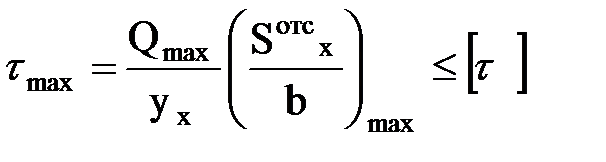 , используя это условие прочности решается два типа задач:
, используя это условие прочности решается два типа задач:
1) Проверочная задача 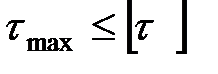
2) Проектировочная задача НЕ РЕШАЕТСЯ, т.к. размеры сечения определены из условия прочности по нормальным напряжениям.
3) Определение несущей способности балки Qmax 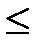 ….
….
Учитывая , что в поперечных сечениях балки одновременно возникают и касательные и нормальные напряжения необходимо дополнительно проверить прочность балки по главным напр.,используя при этом III теорию прочности для Пл.С.
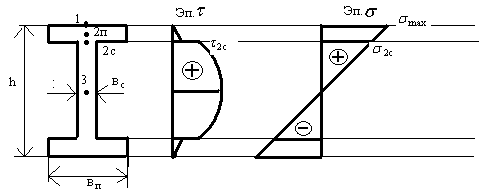 Для сплошных сечений типа прямоугольник и ему подобные, величина
Для сплошных сечений типа прямоугольник и ему подобные, величина 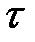 много меньше, чем
много меньше, чем 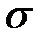 и поэтому такие сечения по главным напр. НЕ проверяются. Для сечений типа двутавр, проверка ОБЯЗАТЕЛЬНА и производится для точки 2С, в которой и норм. и касат. напряжения большие по величине.
и поэтому такие сечения по главным напр. НЕ проверяются. Для сечений типа двутавр, проверка ОБЯЗАТЕЛЬНА и производится для точки 2С, в которой и норм. и касат. напряжения большие по величине.
Проверку по главным напряжениям выполняем, используя след. условие прочности:
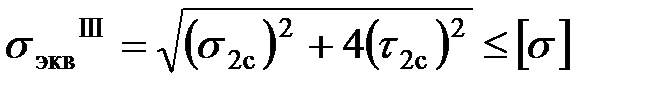
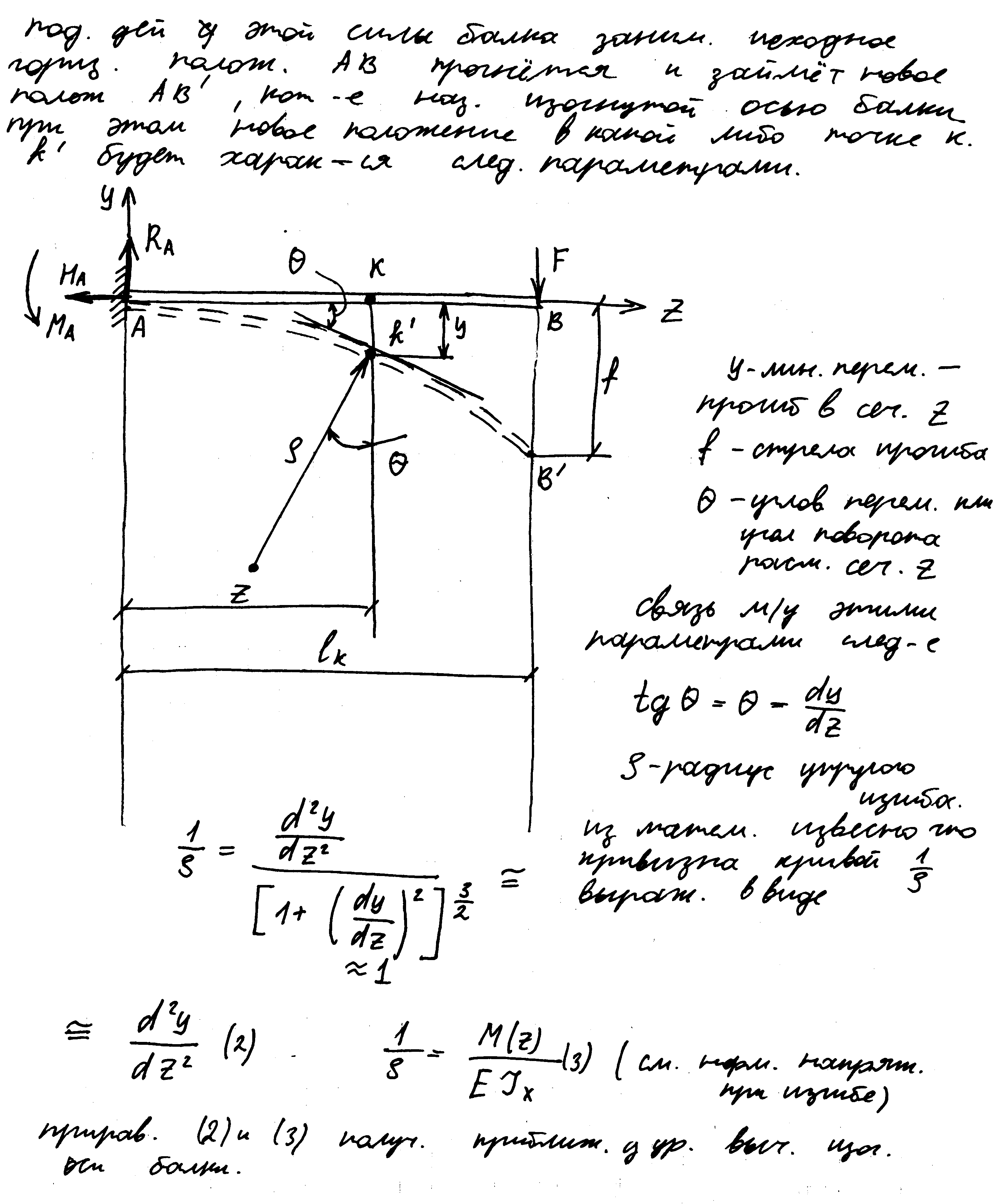
Определение перемещений при изгибе. Условие жесткости. Дифференциальное уравнение изогнутой оси балки.


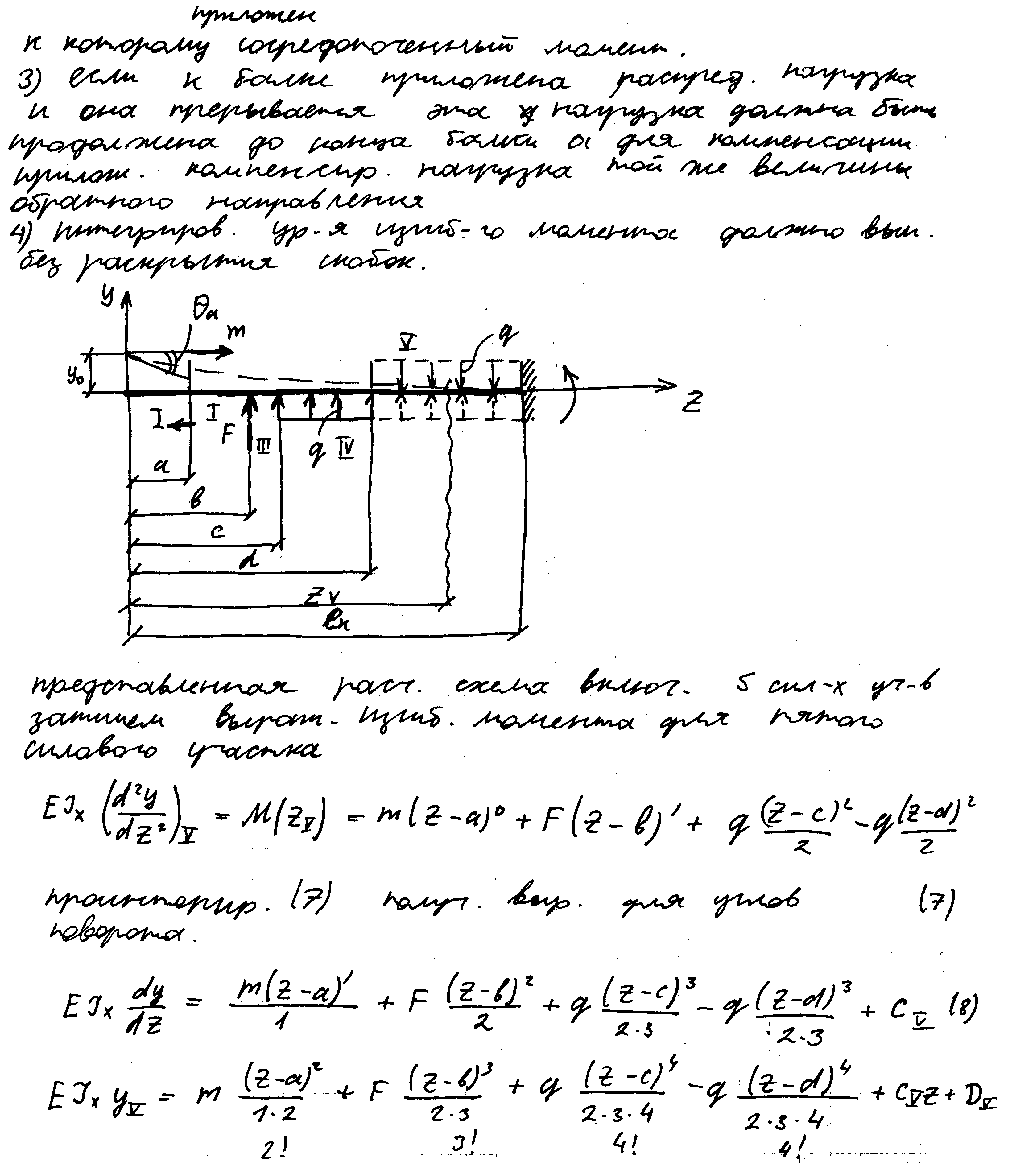
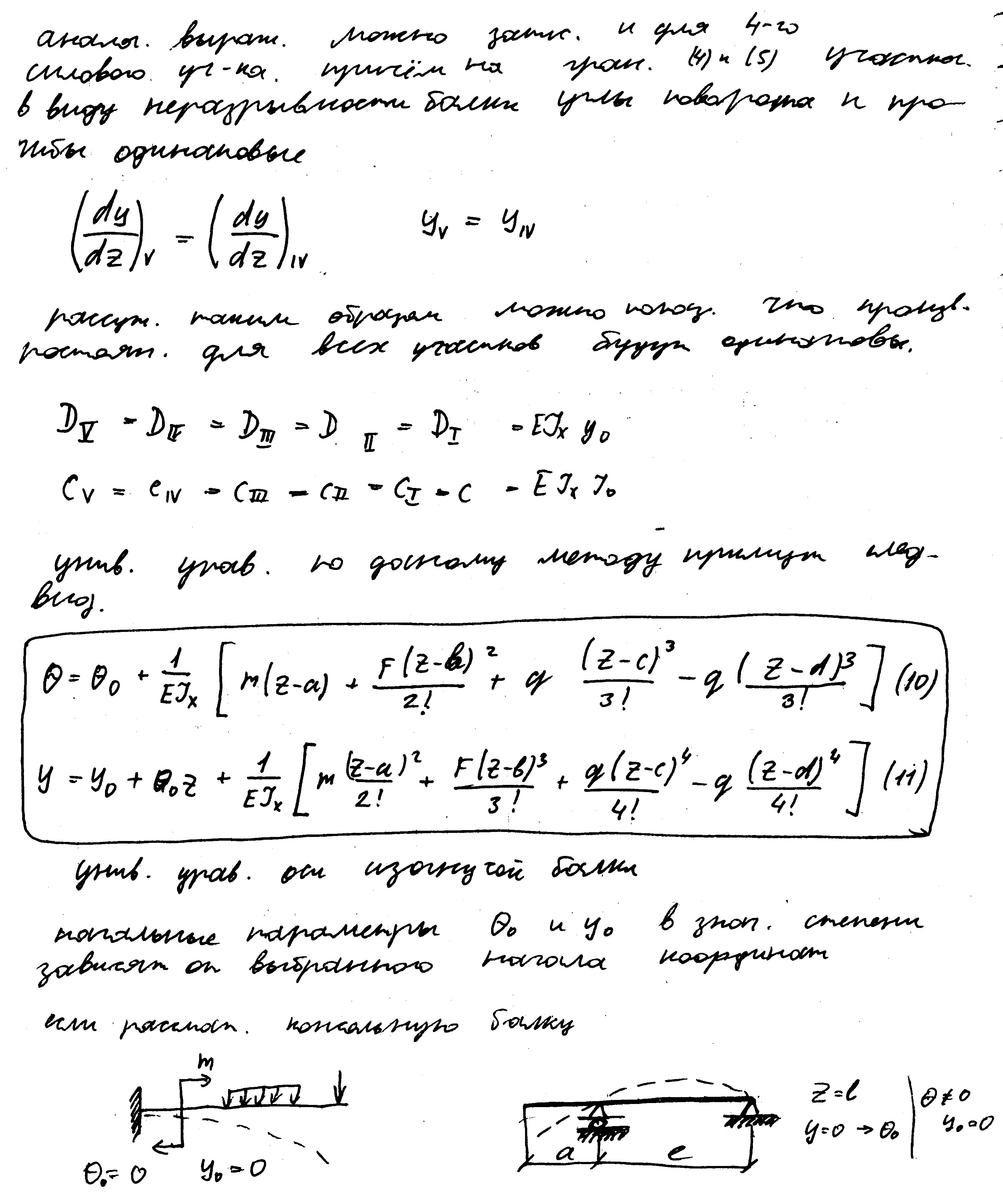
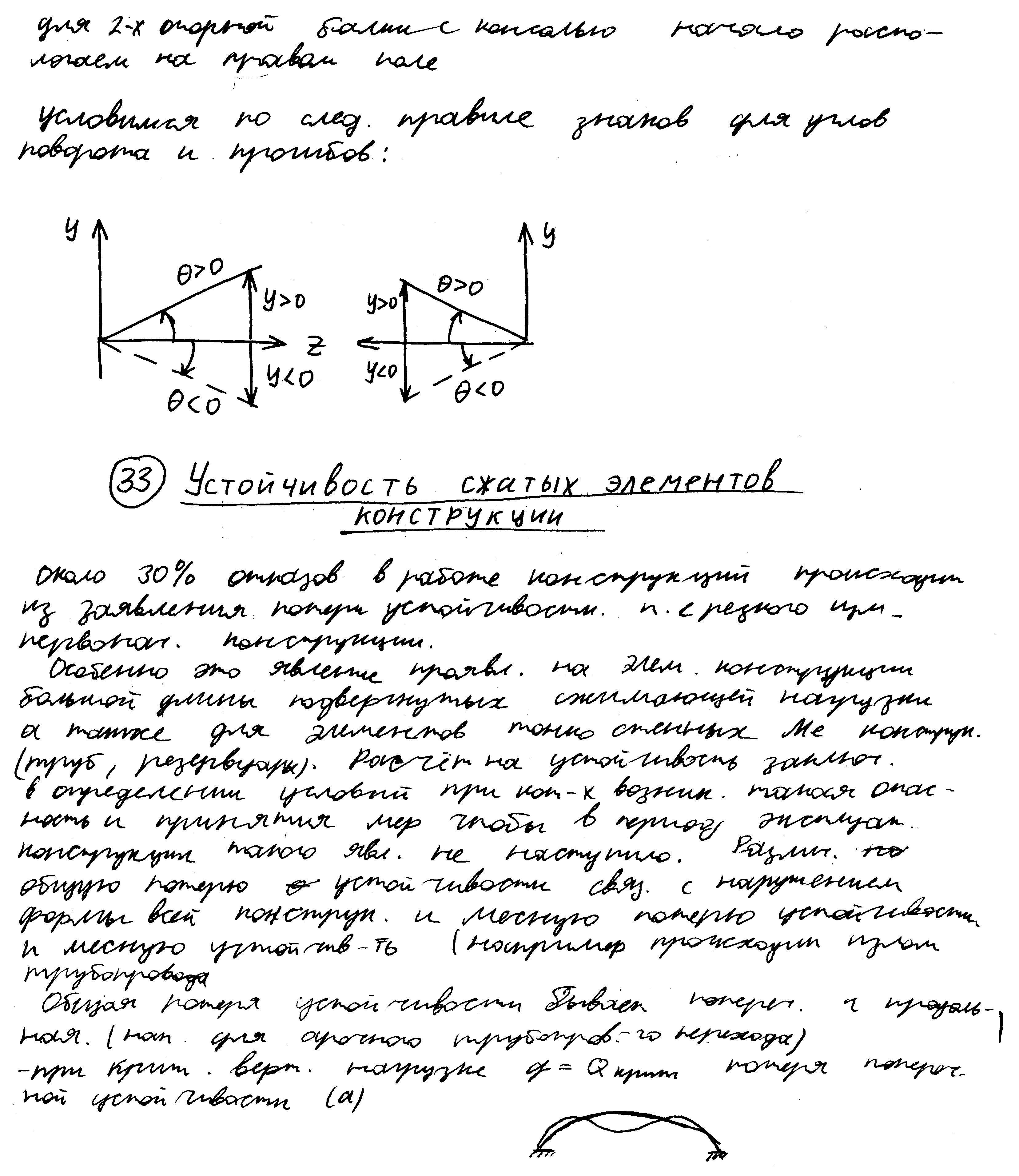
Касательные напряжения при поперечном изгибе.
При поперечном изгибе балок кроме изгибающего момента в поперечных сечениях возникает и 2-й внутренний силовой фактор поперечная сила, которая вызывает появление касательных напряжений, как в плоскости самого поперечного сечения ,так и по закону парности напряжения в продольных волокнах, вызывая их сдвиг, именно эти напряжения явились причиной разрушения нескольких деревянных мостов на ж/д
Санкт - Петербург- Москва.
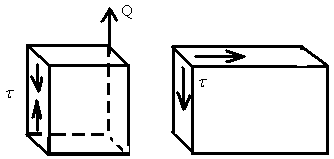
В 1855г. Д.И. Журавский получил следующую зависимость для определения касательных напряжений при поперечном изгибе балок.
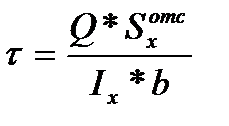
Q- поперечная сила (берём с эпюры Q с соответствующим знаком).
S 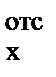 - статический момент отсечённой части сечения на уровне определяемых касательных напряжений.
- статический момент отсечённой части сечения на уровне определяемых касательных напряжений.
I 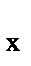 -момент инерции всего поперечного сечения балки.
-момент инерции всего поперечного сечения балки.
b- ширина балки.
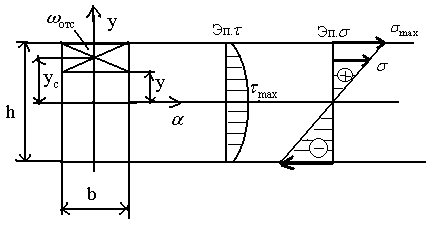
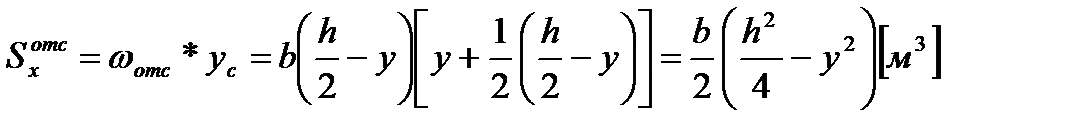
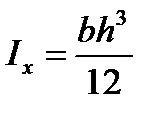
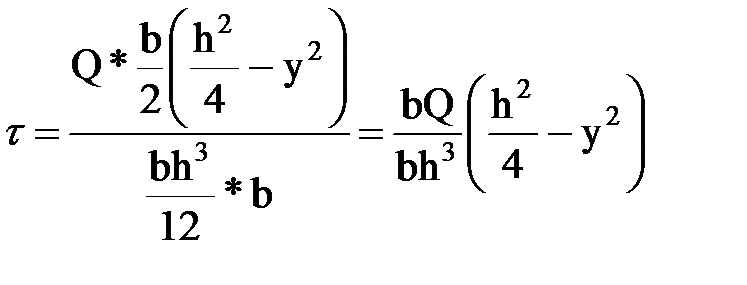
-параболический закон изменения 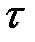 по высоте балки.
по высоте балки.
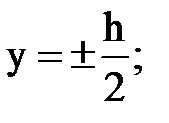
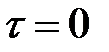
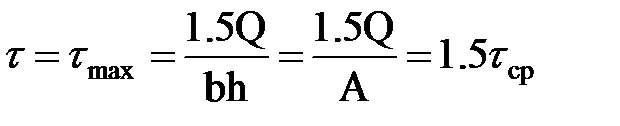
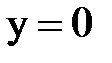
Рассмотрим использование формулы Журавского на примере прямоугольного сечения с размерами b и h. Требуется определить величину касательных напряжений на удалении оси y от оси x.
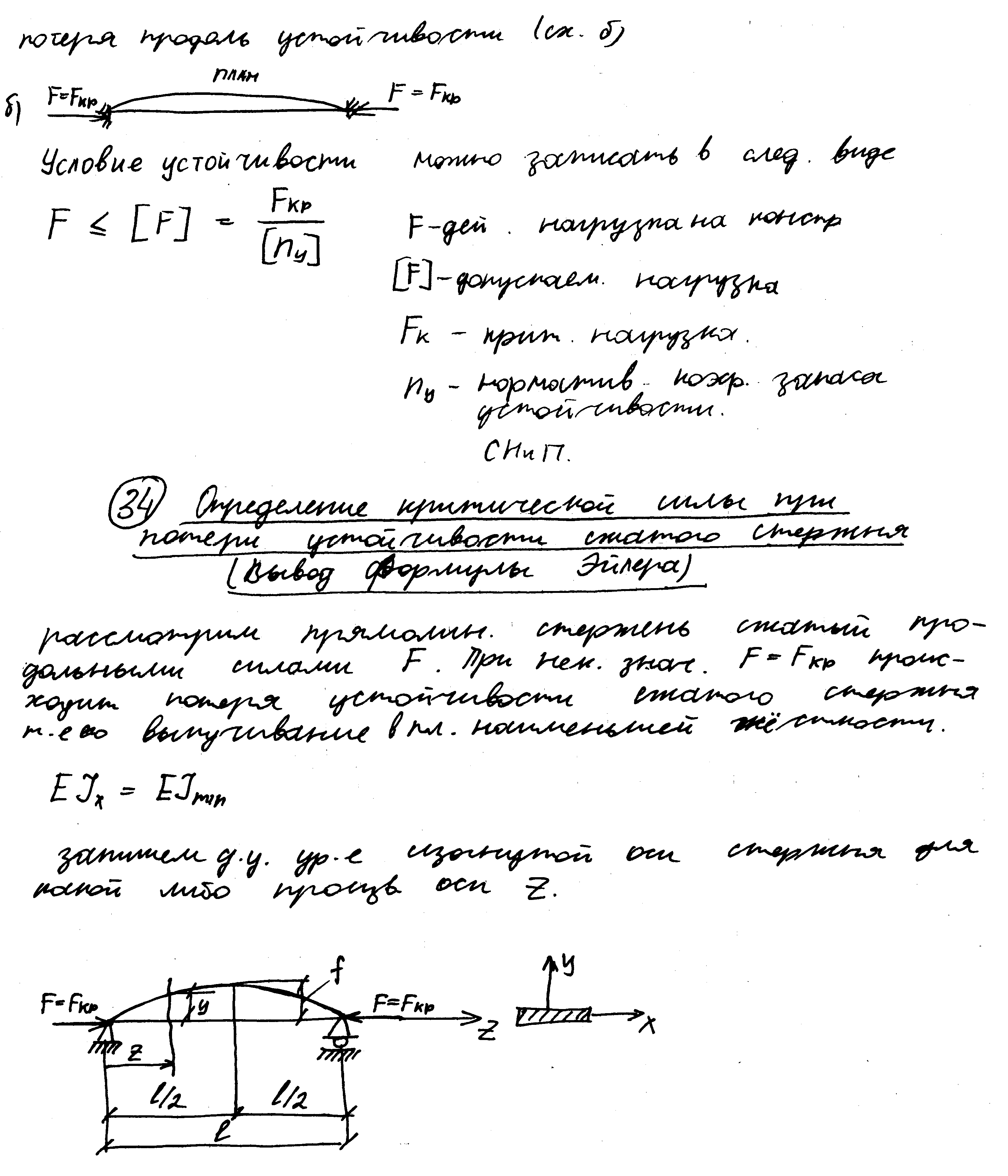
34.Определение критической силы при потере устойчивости сжатого стержня(вывод формулы Эйлера).Пусть стержень длиной L шарнирно опертый сжат продольными силами F.При некотором значении F=Fкр плоскости наим. Жесткости EJmin происходит выпучивание стержня т.е. он теряет продольную устойчивость.
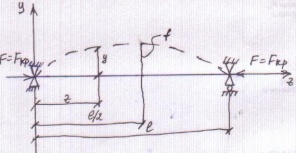
Запишем диф.уравнение изогнутой оси стержня для произвольной оси Z.
EJmin 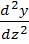 =
= 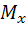 (z)=-Fкр.J
(z)=-Fкр.J
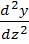 +
+ 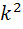 y=0 (2)
y=0 (2)
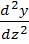 +
+ 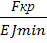 y=0
y=0
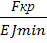 =
= 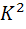
Однородн. диф. Уравнение 2 порядка.Решение уравнения (2) ищем в виде:
y=C1*sinkz + C2*coskz
1) z=0, y=0, C2=0
2) z=L, y=0; 0=C1*sinkz
C1≠0 т.к. стержень изогнутый
sinkL=0, kL=(1…n) π=nπ
3)K= 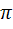 n
n
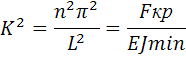
Fкр= 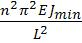 (3)
(3) 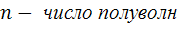
n-1
Fкр= 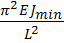 (4) – формула Эйлера получена в 1744г
(4) – формула Эйлера получена в 1744г
