Понятие о напряжениях, деформациях и перемещениях.

Рабочие гипотезы СОПРОМАТА

ОТВЕТ: В отличие от термеха, базирующегося на модели абс. твердого тела, в сопромате принята своя расчетная модель-модель идеализированного деформируемого тела. А для упрощения расчетов принимаются следующие допущения или гипотезы: 1) Материал тела имеет сплошное строение. 2) материал однороден, т.е. во всех точках свойства одинаковы. 3) материал изотропен, т.е. по всем направлениям свойства одинаковы. 4) до приложения внешних сил начальные напряжения в материале отсутствуют. 5) при решении реальных задач целесообразно использовать принцип суперпозиции, или принцип независимости действия сил, т.е. воздействие на конструкцию группы сил равно сумме воздействий от каждой силы в отдельности и не зависит от последовательности приложения этих сил.

ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ И МЕТОД ИХ ОПРЕДЕЛЕНИЯ.

ОТВЕТ: Под действием внешних сил на брус возникают внутренние силы или внутренние силовые факторы, для определения которых в сопромате принят единый расчетный метод – метод сечений. 1) разрезаем мысленно брус в исследуемом сечении на 2 части I и II. 2) Отбрасываем одну из частей. 3) Заменяем действие отбрасываемой части II на часть I внутренними силовыми факторами(в общем случае их 6). Q_x Q_y – поперечные силы, N_z – продольная сила, M_x M_y – изгибающие моменты, M_z – крутящий момент. 4) Уравновешиваем оставшуюся часть бруса и с помощью уравнений равновесия термеха находим искомые силовые факторы.

ПОНЯТИЕ О НАПРЯЖЕНИЯХ, ДЕФОРМАЦИЯХ И ПЕРЕМЕЩЕНИЯХ.

ОТВЕТ: Мерой интенсивности действия внутренних сил в окрестности точки рассматриваемого поперечного сечения являются напряжения, определяемые отношением силы к единице площади [Па]. Если в поп. сечении выделить элемент DА, к которому будет приложена сила DР, то DР/DА=р_m – среднее полное напряжение в рассматриваемой точке поперечного сечения. 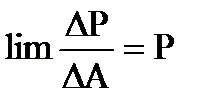- полное истинное напряжение. Вектор 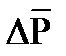раскладывают на 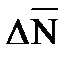и . 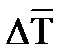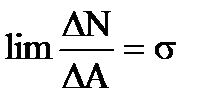- нормальное напряжение – вызывает разрушения путем отрыва. 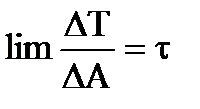- касательное напряжение – вызывает разрушение путем сдвига. Перемещения и деформации – понятия, характеризующие изменение размеров и формы исследуемого тела. При этом перемещения являются следствием деформации.

Напряжения и деформации при кручении вала круглого поперечного сечения.

Определение деформаций.

При кручении как было отмечено выше лин. деформаций не происходит,и под действием касат. напряжений 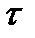происходит перенос сетки(квадраты становятся ромбами, при этом max величины переноса - абсолютный 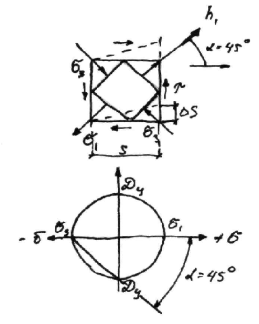сдвиг, а отношение 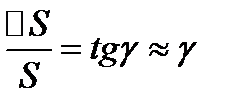- относит. 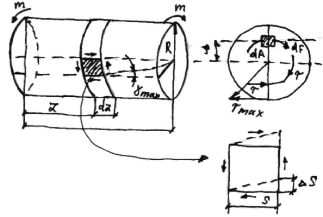сдвиг.

По аналогии с растяжением сжатием:

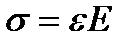( ) З-Н Гука применительно к кручению: 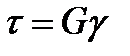(1) G – модуль упругости II рода

Связь м/у модулями II рода: 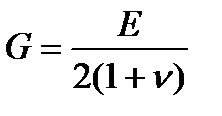, для стали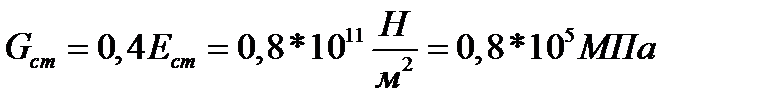

Определение перемещений при изгибе. Условие жесткости. Дифференциальное уравнение изогнутой оси балки.

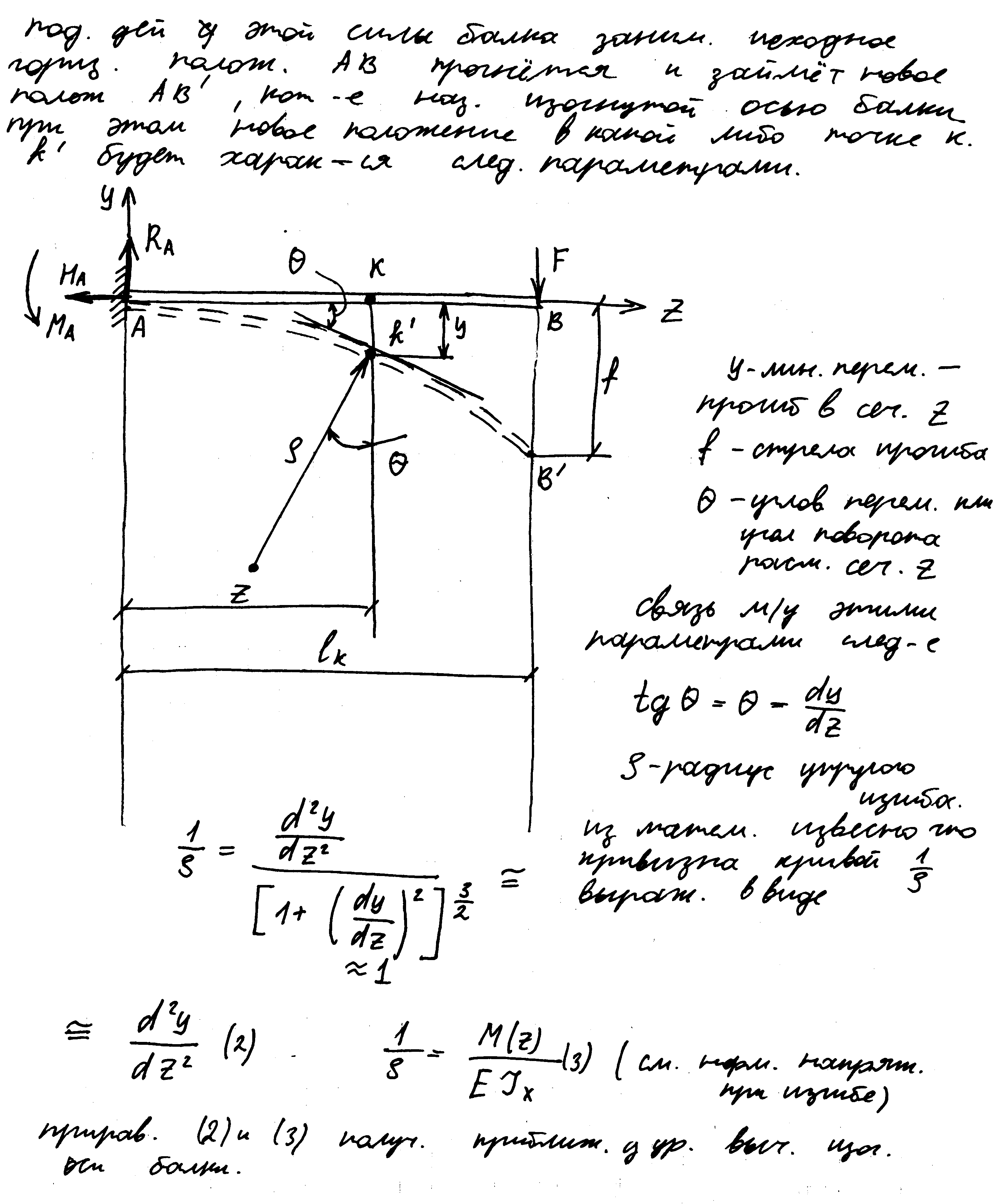
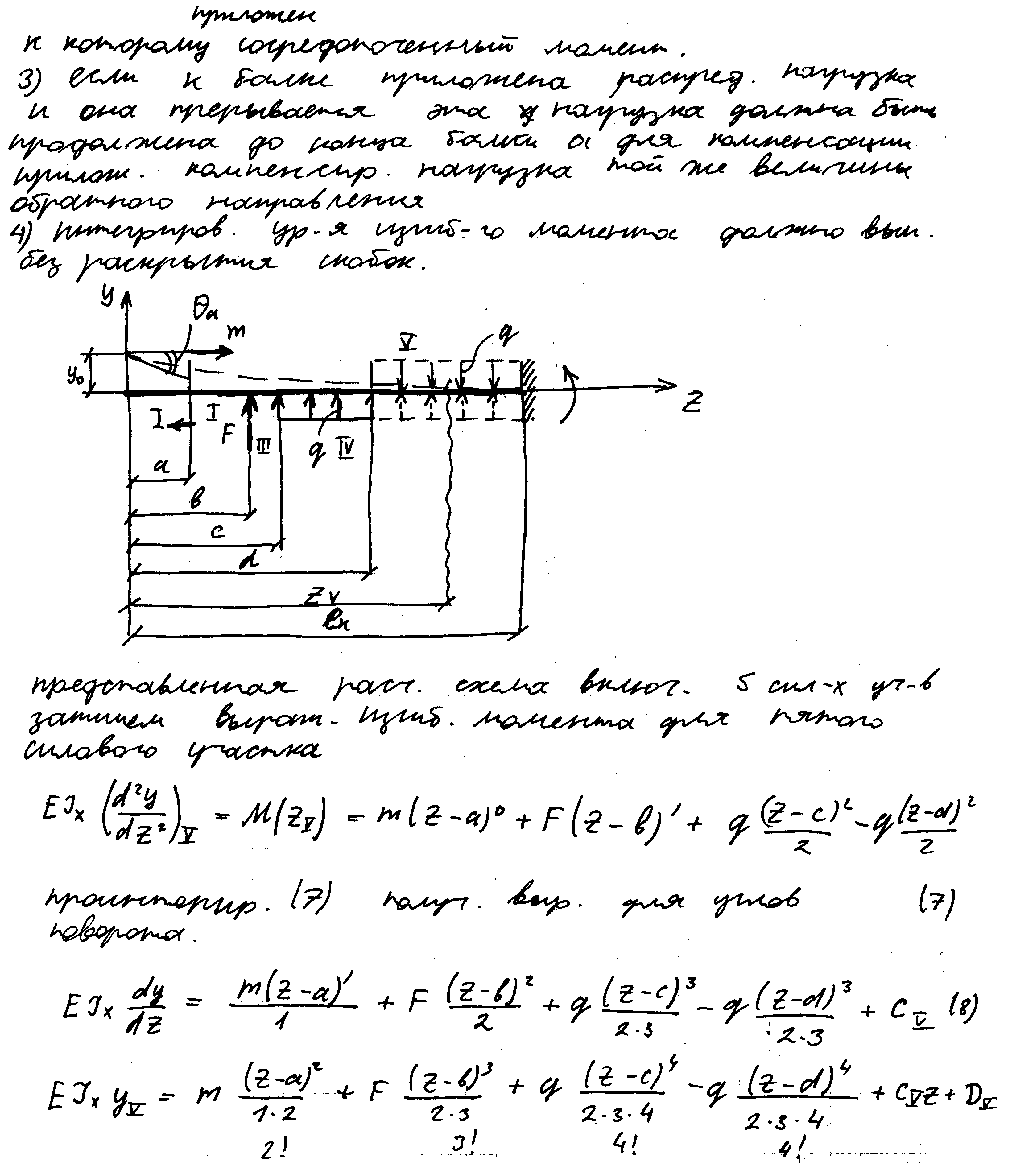
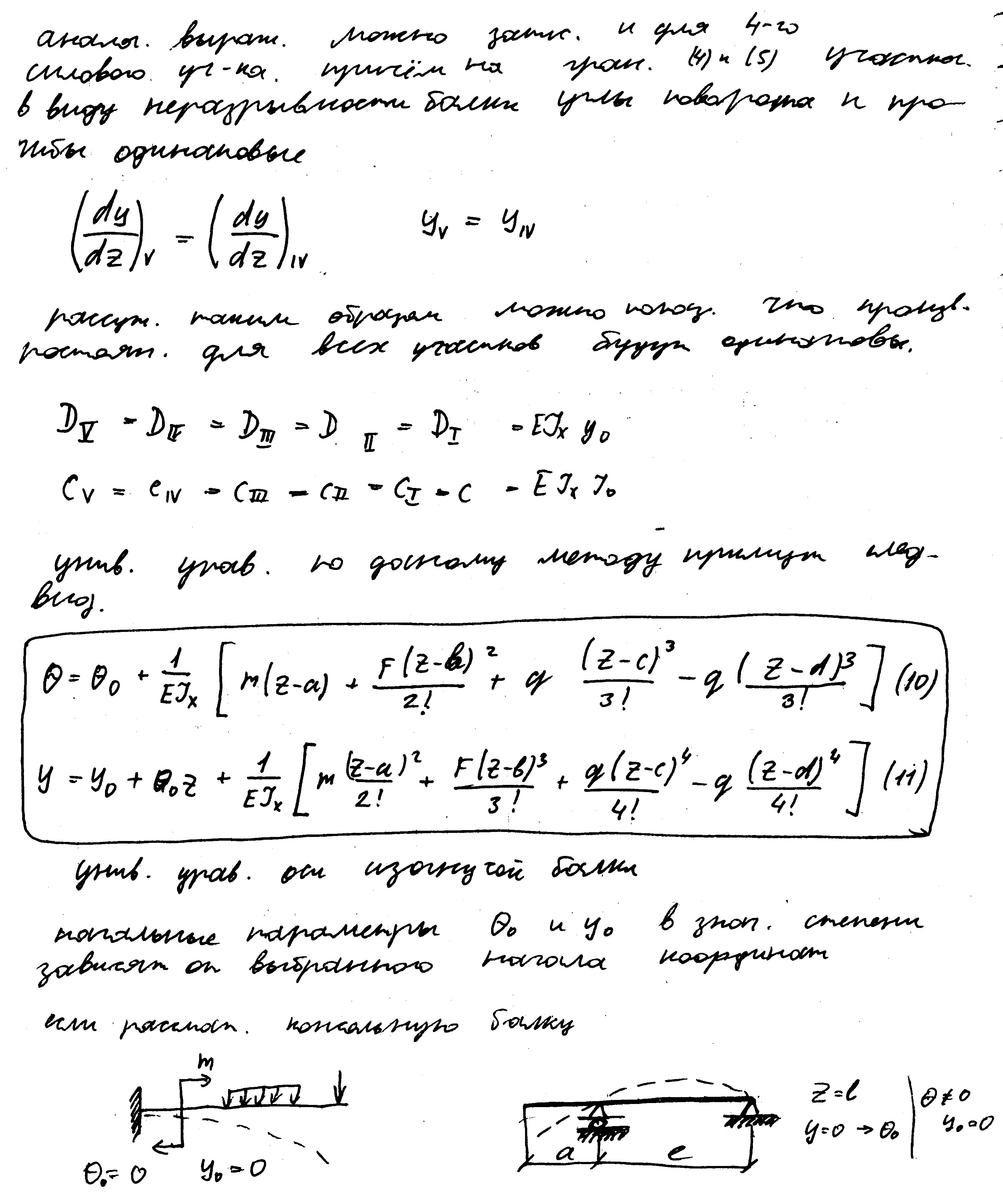
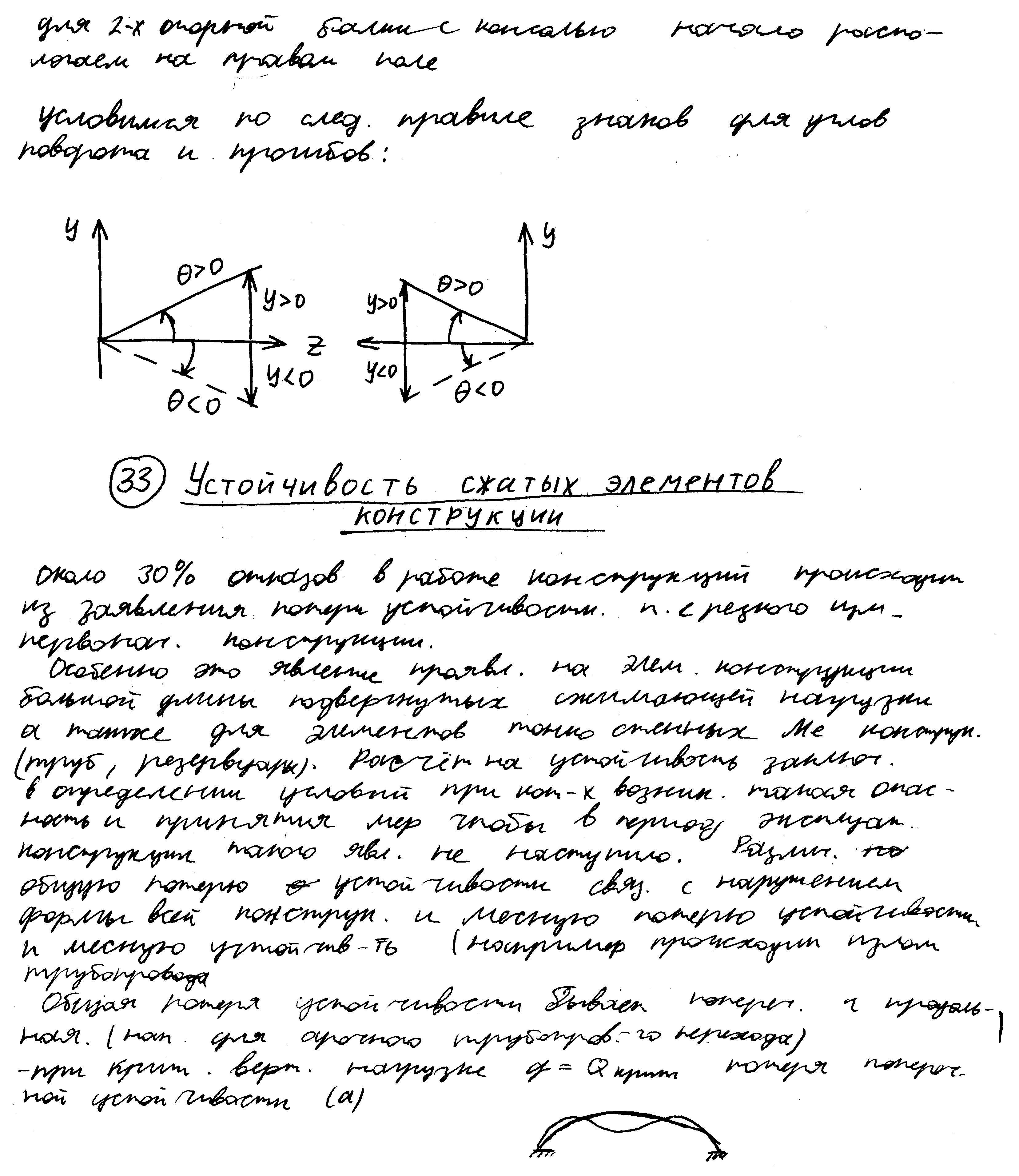
Варианты расчета простых статически неопределимых балок

Существует несколько способов расчета простых балок:

1.Сравнение линейных перемещений.

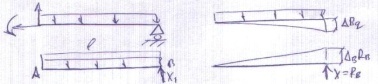
ΔВ=ΔВq+ΔBRB=0(1) доп. уравнение деформаций

Слагаемые в(1) могут быть найдены исп-я готовые таблицы или универсальные уравнения. Применительно к рас-му предмету:

ΔBq=-qe⁴/8EIx; ΔBRB=RBe³ /3EIx;

ΔB=-qe⁴/8EIx +RBe³/3EIx =0 =>RB=3qe/8

2. Сравнение угловых перемещений.

Можно отбросить связь, препятствующая повороту опорного сечения А и записать

ΔA=ΔAq+ΔAMA=0(2)

Также ур-е деформации слагаемое означает углы поворота.

3.Составление замкнутой системы ур-я.

3 ур-я статики+ унивес. ур-е

yB=0.

43. Метод сил для расчета сложных СНС.

Метод при котором за неизвестное принимаются сосредоточенные моменты наз-ся методом сил. Он явл-ся наиболее распространенным и ис-ся для любых упругих систем (балки, рамы,эстакады итд.).

Например: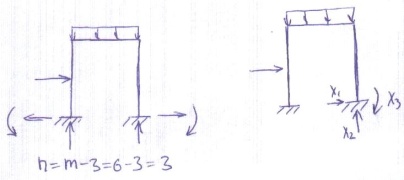

К трем ур-ям статики для решения данной СНС добавится 3 уравнения, выражающие рав-во 0 перемещений по направлениям всех отброшенных связей т.е. опорное сечение и не перемещаются им в горизонтальном или в вертикальном перемещениях и не переворачиваются.

X1 Δ1=0

X2 Δ2=0 (1)

X3 Δ3=0

Каждое уравнение системы(1) можно записать в развернутом виде:

Δ1=Δ11+Δ12+Δ13+Δ1f=0 (2)

Первый символ указывает направление; 2-й воз-е.

Δ1f-перемещение опорного сечения А в направлении действия X, вызванное внешней нагрузкой

(2) можно выразить через единичные перемещения и искомое неизвестное (это первые три слагаемых)

Δ11=δ11-x1 и тогда система примет закончен. вид.

δ11 x1+ δ12 x2+ δ13 x3+ Δ1f=0

δ21 x1+ δ22 x2+ δ23 x3+ Δ2f=0 (3)-система кумс.

δ31 x1+ δ32 x2+ δ33 x3+ Δ3f=0

Канонические ур-я метода сил-КУМС.

Число ур-й равно степени статической неопределимости.

Рабочие гипотезы СОПРОМАТА

ОТВЕТ: В отличие от термеха, базирующегося на модели абс. твердого тела, в сопромате принята своя расчетная модель-модель идеализированного деформируемого тела. А для упрощения расчетов принимаются следующие допущения или гипотезы: 1) Материал тела имеет сплошное строение. 2) материал однороден, т.е. во всех точках свойства одинаковы. 3) материал изотропен, т.е. по всем направлениям свойства одинаковы. 4) до приложения внешних сил начальные напряжения в материале отсутствуют. 5) при решении реальных задач целесообразно использовать принцип суперпозиции, или принцип независимости действия сил, т.е. воздействие на конструкцию группы сил равно сумме воздействий от каждой силы в отдельности и не зависит от последовательности приложения этих сил.

ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ И МЕТОД ИХ ОПРЕДЕЛЕНИЯ.

ОТВЕТ: Под действием внешних сил на брус возникают внутренние силы или внутренние силовые факторы, для определения которых в сопромате принят единый расчетный метод – метод сечений. 1) разрезаем мысленно брус в исследуемом сечении на 2 части I и II. 2) Отбрасываем одну из частей. 3) Заменяем действие отбрасываемой части II на часть I внутренними силовыми факторами(в общем случае их 6). Q_x Q_y – поперечные силы, N_z – продольная сила, M_x M_y – изгибающие моменты, M_z – крутящий момент. 4) Уравновешиваем оставшуюся часть бруса и с помощью уравнений равновесия термеха находим искомые силовые факторы.

ПОНЯТИЕ О НАПРЯЖЕНИЯХ, ДЕФОРМАЦИЯХ И ПЕРЕМЕЩЕНИЯХ.

ОТВЕТ: Мерой интенсивности действия внутренних сил в окрестности точки рассматриваемого поперечного сечения являются напряжения, определяемые отношением силы к единице площади [Па]. Если в поп. сечении выделить элемент DА, к которому будет приложена сила DР, то DР/DА=р_m – среднее полное напряжение в рассматриваемой точке поперечного сечения. 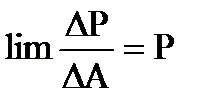- полное истинное напряжение. Вектор 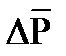раскладывают на 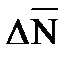и 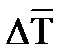. 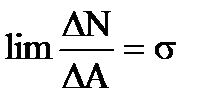- нормальное напряжение – вызывает разрушения путем отрыва. 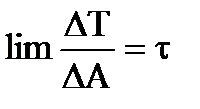- касательное напряжение – вызывает разрушение путем сдвига. Перемещения и деформации – понятия, характеризующие изменение размеров и формы исследуемого тела. При этом перемещения являются следствием деформации.