Определение производной, зависимость между непрерывностью и дифференцируемостью функции

Рассмотрим y=y(x) на промежутке x, возьмём т.хp wsp:rsidR="00000000" wsp:rsidRDefault="00E45C86"><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="10"/><w:sz-cs w:val="10"/></w:rPr><m:t>Пµ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1417" w:right="1417" w:bottom="1417" w:left="1417" w:header="708" w:footer="708" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> Х и придадим точке приращение х>0. Тогда мы получим приращение ф-ии,кот.обознач-ся у=f(x+ х)-f(x). Производной ф-ии у=f(x) наз-ся предел отношения приращения ф-ии к приращению аргумента,при приращении аргумента стремящимся к 0(если предел сущ-т). y’-производная ф-ия, y’= = 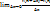. если ф-ия в т.х им.конечную производную, то она наз-ся дифференцируемой в т.х. Если ф-ия дифференцируема в каждой точке промежутка Х,то она наз-ся диффер-мой на промежутке. Смысл производной геометрический: знач-е производной f’ ) в т.касания есть угловой коэфиц-т касательной,проведённой к ф-ии y=f(x).

Т.если ф-ия диффер-ма в т. , то она непрерывна в этой точке.

Схема вычисления производной, основные правила дифференцирования

Производной функции f(x) в точке х = х₀ называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.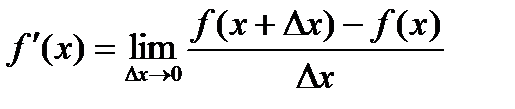

Пусть f(x) определена на некотором промежутке (a, b). Тогда 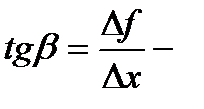тангенс угла наклона секущей МР к графику функции.

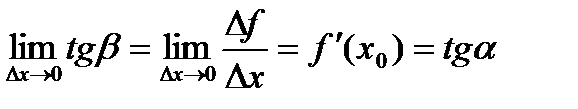, где a - угол наклона касательной к графику функции f(x) в точке (x₀, f(x₀)). Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой: 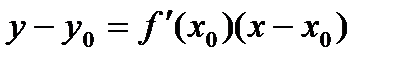. Ур-е нормали к кривой: .

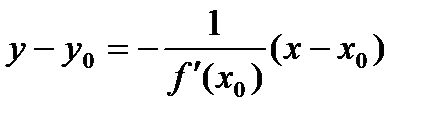Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.

Основные правила дифференцирования.

Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.

1)С¢ = 0, где с-число

2) (u ± v)¢ = u¢ ± v¢

3) (u×v)¢ = u×v¢ + u¢×v

4) 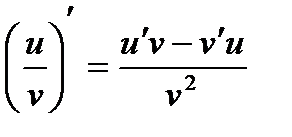, если v ¹ 0

5)производн. аргумента x’=1

Производная сложной функции. Производная обратных функций.

Пусть y=f(u),a u=g(x). тогда задана сложн.ф-ия y=f(g(x))

Т.если y = f(x); u = g(x) дифференцируемы от своих аргументов, то производная сложн.ф-ии нах-ся по фомуле у’=f’(g(x))*g’(x)

Производная обратных функций.

Пусть требуется найти производную функции у = f(x) при условии, что обратная ей функция x = g(y) имеет производную, отличную от нуля в соответствующей точке.

Для решения этой задачи дифференцируем функцию x = g(y) по х:

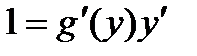, т.к. g¢(y) ¹ 0 , ,

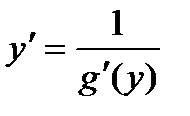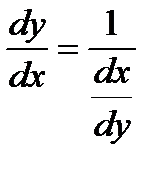
т.е. производная обратной функции обратна по величине производной данной функции.