Предел функции в точке и на бесконечности
Определение по Коши
Число А называется пределом функции f(x) в точке х0, если функция определена в некоторой выколотой окрестности точки х0 и если для любого сколь угодно малого числа 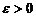 существует такое число
существует такое число 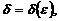 что для всех х, удовлетворяющих условию
что для всех х, удовлетворяющих условию
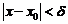 (1)
(1)
выполняется
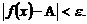 (2)
(2)
Это записывают:
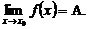
Число А называется пределом функции на бесконечности, если для любого 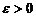 существует число
существует число 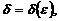 что для всех х, удовлетворяющих условию
что для всех х, удовлетворяющих условию
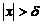
выполняется неравенство
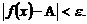
Это записывают:
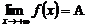 (
( 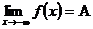 ).
).
Определение предела функции в точке (на бесконечности) по Гейне и по Коши эквивалентны.
Функция f(x) называется бесконечно большой при 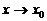
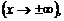 если для всякого числа М > 0 существует
если для всякого числа М > 0 существует 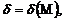 что для всех х, удовлетворяющих условию
что для всех х, удовлетворяющих условию
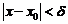 (
( 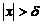 )
)
выполняется неравенство
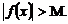
Это записывают:
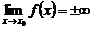
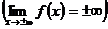 .
.
Если f(x) – бесконечно большая функция при 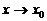
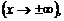 то она не имеет предела в этой точке (на бесконечности). Символ предела в данном случае используют лишь для обозначения.
то она не имеет предела в этой точке (на бесконечности). Символ предела в данном случае используют лишь для обозначения.
Функция f(x) называется бесконечно малой при 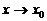
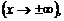 если
если
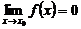
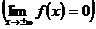 .
.
Свойства предела функции в точке
1. Если функция f(x) имеет предел в точке х0, то существует окрестность этой точки (за исключением, быть может, самой точки х0), на которой функция ограничена.
2. Если существует предел функции f(x) в точке х0, равный 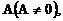 то существует такая окрестность точки х0, на которой функция имеет тот же знак, что и А.
то существует такая окрестность точки х0, на которой функция имеет тот же знак, что и А.
3. Если функции f(x) и g(x) имеют пределы в точке х0, то:
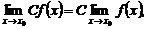 где
где 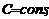
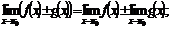 (3)
(3)
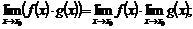 (4
(4
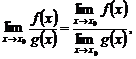 где
где 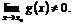 (5)
(5)
Аналогичные свойства верны и для предела функции на бесконечности.
Если в результате непосредственного использования формул (3)–(5) возникает неопределенность типа 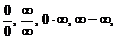 то вначале необходимо тождественно преобразовать выражение, стоящее под знаком предела (то же для неопределенностей
то вначале необходимо тождественно преобразовать выражение, стоящее под знаком предела (то же для неопределенностей 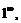
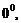
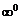 ).
).
Свойства бесконечно малых и бесконечно больших функций
1. Число А является пределом функции f(x) в точке х0 тогда и только тогда, когда существует бесконечно малая функция 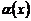 при
при 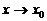 такая, что
такая, что 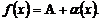 .
.
2. Сумма и произведение конечного числа бесконечно малых (бесконечно больших) функций при 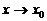 является бесконечно малой (бесконечно большой функцией).
является бесконечно малой (бесконечно большой функцией).
3. Произведение бесконечно малой при 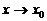 функции на ограниченную функцию является бесконечно малой.
функции на ограниченную функцию является бесконечно малой.
4. Частное при делении постоянной С, 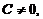 на бесконечно малую при
на бесконечно малую при 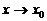 является бесконечно большой при
является бесконечно большой при 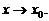
5. Частное при делении постоянной С на бесконечно большую при 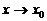 является бесконечно малой при
является бесконечно малой при 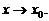
При вычислении пределов функций удобно применять метод замены переменной, т.е. 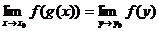 , где
, где 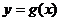 , если
, если 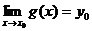 .
.
Замечательные пределы
При вычислении пределов в случае неопределенностей часто используют специальные формулы, которые называются замечательными пределами.
В 31.Первый замечательный предел
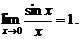 (7)
(7)
Как следствие формулы (7) справедливы формулы
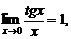
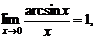
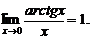
Второй замечательный предел
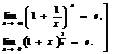 (8)
(8)
Третий замечательный предел
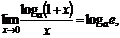 (9)
(9)
в частности,
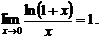
Четвертый замечательный предел
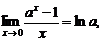 (10)
(10)
в частности,
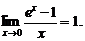
Пятый замечательный предел
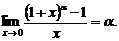 (11)
(11)
Указанные формулы (7)–(11) замечательных пределов обобщаются на любую функцию u(x), стоящую вместо независимой переменной х при условии, что 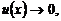 если
если 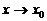 (или
(или 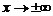 ) во всех формулах кроме (8), в которых
) во всех формулах кроме (8), в которых 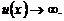
Обобщенная таблица замечательных пределов
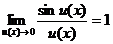 ;
;
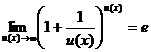 ;
; 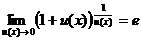 ; (12)
; (12)
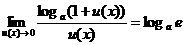 ;
; 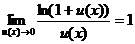 ; (13)
; (13)
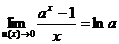 ;
; 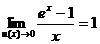 ; (14)
; (14)
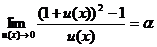 . (15)
. (15)
При использовании обобщенных форму на практике вместо 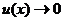
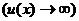 (под знаком предела пишут указанное в условии:
(под знаком предела пишут указанное в условии: 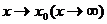 .
.
Все приведенные формулы обобщенной таблицы замечательных пределов (кроме формул (12)) раскрывают неопределенность типа 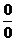 . Формулы (12) раскрывают неопределенность типа
. Формулы (12) раскрывают неопределенность типа 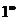 .
.
Эквивалентность функции
Две функции  и
и 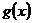 называются эквивалентными бесконечно малыми, при
называются эквивалентными бесконечно малыми, при 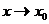
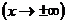 , если
, если
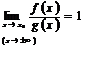 ,
,
это записывают 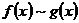 при
при 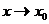
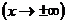 .
.
При вычислении пределов функций в точке и на бесконечности удобно пользоваться следующей теоремой:
Если 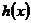 ,
,  и
и 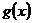 - некоторые функции, определенные в
- некоторые функции, определенные в
окрестности точки  (на числовой полуоси) и
(на числовой полуоси) и 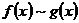 при
при
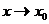
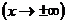 , то
, то
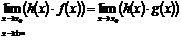 . (16)
. (16)
Формула (16) показывает, что в произведении можно заменять функцию – сомножитель на эквивалентную ей – более простую для вычисления предела.
Таблица эквивалентных бесконечно малых
Пусть 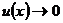 , если
, если 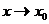
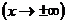 . Тогда справедливы следующие эквивалентности:
. Тогда справедливы следующие эквивалентности:
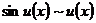 ; (17)
; (17)
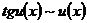 ; (18)
; (18)
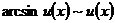 ; (19)
; (19)
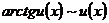 ; (20)
; (20)
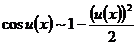 ; (21)
; (21)
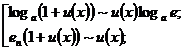 (22)
(22)
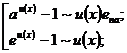 (23)
(23)
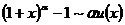 (24)
(24)
