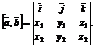В.15 Линейная зависимость векторов. Действиянад векторами в координатной форме
Векторы 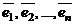 называются линейно независимыми, если равенство
называются линейно независимыми, если равенство
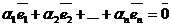
справедливо тогда и только тогда, когда 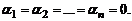 В противном случае эти векторы называются линейно зависимыми. Для того чтобы векторы
В противном случае эти векторы называются линейно зависимыми. Для того чтобы векторы 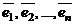 были линейно зависимыми, необходимо и достаточно, чтобы хотя бы один из них можно было представить в виде линейной комбинации остальных.
были линейно зависимыми, необходимо и достаточно, чтобы хотя бы один из них можно было представить в виде линейной комбинации остальных.
Упорядоченная тройка 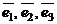 ненулевых линейно-независимых векторов образует базис в трехмерном пространстве. Любой вектор
ненулевых линейно-независимых векторов образует базис в трехмерном пространстве. Любой вектор  пространства единственным образом может быть разложен по базисным векторам, т.е. представлен в виде
пространства единственным образом может быть разложен по базисным векторам, т.е. представлен в виде
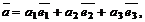
где 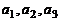 – координаты вектора
– координаты вектора 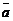 в базисе
в базисе 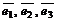 (записывают:
(записывают: 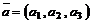 ).
).
В пространстве линейная независимость векторов равносильна их некомпланарности, т.е. любые три некомпланарных вектора, взятые в определенном порядке, образуют базис.
Пусть задана тройка 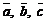 некомпланарных векторов. Совместим начала этих векторов. Если кратчайший поворот вектора
некомпланарных векторов. Совместим начала этих векторов. Если кратчайший поворот вектора 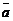 до направления вектора
до направления вектора 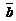 , наблюдаемый с конца вектора
, наблюдаемый с конца вектора 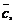 совершается против часовой стрелки, то тройка векторов
совершается против часовой стрелки, то тройка векторов 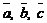 называется правой. В противном случае – левой. Всюду далее рассматриваются правые тройки базисных векторов.
называется правой. В противном случае – левой. Всюду далее рассматриваются правые тройки базисных векторов.
Совокупность базисных векторов и их общего начала образуют, аффинную систему координат в пространстве. Координаты векторов в таком случае называют аффинными.
Если даны два вектора 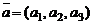 и
и 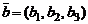 в некотором базисе, то
в некотором базисе, то
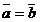 тогда и только тогда, когда
тогда и только тогда, когда 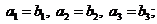
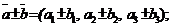 (2)
(2)
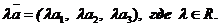 (3)
(3)
В случае, когда базисные векторы попарно перпендикулярны, система координат называется прямоугольной декартовой. Если добавить, кроме того, условие нормированности базисных векторов (т.е. их единичную длину), то такой базис называют ортонормированным и обозначают 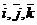 :
: 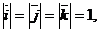
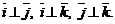 Прямоугольные декартовы координаты вектора
Прямоугольные декартовы координаты вектора  является его проекциями на вектора
является его проекциями на вектора 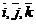 соответственно.
соответственно.
Если точка M имеет прямоугольные декартовы координаты x, y, z в системе координат с началом в точке O(0, 0, 0) и базисом 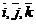 , то соответствующий радиус-вектор
, то соответствующий радиус-вектор
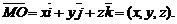
Если 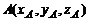 и
и 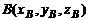 , то
, то
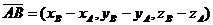 .
.
Линейные операции для векторов  и
и 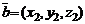 в координатной форме и их скалярное произведение вычисляются по формулам:
в координатной форме и их скалярное произведение вычисляются по формулам:
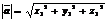 ; (4)
; (4)
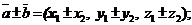 (5)
(5)
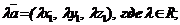 (6)
(6)
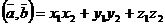 ; (7)
; (7)
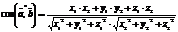 . (8)
. (8)
Направляющими косинусами вектора 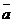 называются величины
называются величины 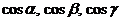 , где
, где 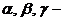 углы, которые образует вектор
углы, которые образует вектор 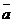 соответственно с осями
соответственно с осями 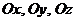 . Их вычисляют по формулам:
. Их вычисляют по формулам:
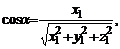
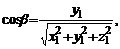 (9)
(9)
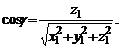
Если  единичный вектор, то
единичный вектор, то 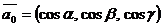 .
.
Координаты точки C, делящей отрезок AB в отношении 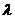 ,
, 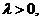 можно найти по формулам:
можно найти по формулам:
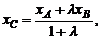
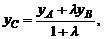
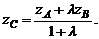
В.13 Векторное произведение
Векторным произведением 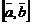 двух векторов
двух векторов 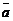 и
и 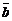 называется вектор, удовлетворяющий следующим условиям:
называется вектор, удовлетворяющий следующим условиям:
1) 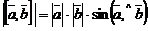 ;
;
2) 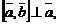
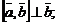
3) тройка векторов 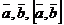 – правая.
– правая.
Векторное произведение обозначают также 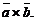
Если хотя бы один из векторов 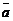 или
или 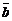 нулевой, то
нулевой, то 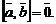
Геометрический смысл векторного произведения 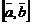 состоит в том, что длина этого вектора численно равна площади параллелограмма, построенного на векторах
состоит в том, что длина этого вектора численно равна площади параллелограмма, построенного на векторах 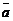 и
и 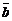 :
:
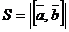 ..
..
Свойства векторного произведения:
1) 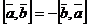 ;
;
2) 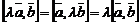 ;
;
3) 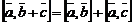 ;
;
4) 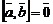 при
при 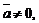
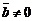 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 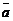 и
и 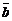 коллинеарны.
коллинеарны.
Если 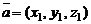 и
и 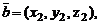 то
то
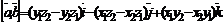
Последнюю формулу удобно записать в виде формального определения третьего порядка: