То есть интеграл по всему отрезку равен сумме интегралов по частям этого отрезка. Это свойство называют аддитивностью определенного интеграла (или свойством аддитивности).
5. Теорема о среднем. Если функция f(x) непрерывна на отрезке [а; b], то существует точка с Î [a.;b] такая, что
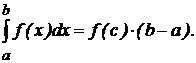
6. Если функция f(x) сохраняет знак на отрезке [а; b], где а <b, то интеграл 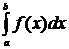 имеет тот же знак, что и функция. Так, если
имеет тот же знак, что и функция. Так, если 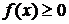 на отрезке [а; b], то
на отрезке [а; b], то 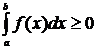 .
.
7. Неравенство между непрерывными функциями на отрезке [а;b],(а < b) можно интегрировать. Отметим, что дифференцировать неравенства нельзя.
8. Оценка интеграла. Если m и M — соответственно наименьшее и наибольшее значения функции у = f(x) на отрезке [а;b], (а < b), то
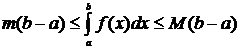 .
.
9. Модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции:
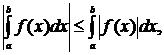 где a<b.
где a<b.
10. Пусть функция y=f(x) непрерывна на отрезке [a;b]. Рассмотрим интеграл 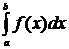 . Значение интеграла зависит от обоих пределов интегрирования a и b.
. Значение интеграла зависит от обоих пределов интегрирования a и b.
Теорема. Производная от интеграла по верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом, то есть
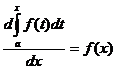 . Данная теорема означает, что функция
. Данная теорема означает, что функция 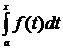 является первообразной для
является первообразной для 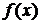 . Из этой теоремы следует, что всякая непрерывная функция
. Из этой теоремы следует, что всякая непрерывная функция 
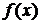 имеет первообразные, одной из которых является интеграл
имеет первообразные, одной из которых является интеграл 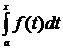 .
.
Формула Ньютона – Лейбница.
Простым и удобным методом вычисления определенного интеграла 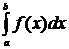 от непрерывной функции является формула Ньютона-Лейбница:
от непрерывной функции является формула Ньютона-Лейбница:
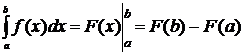 .
.
Применяется этот метод во всех случаях, когда может быть найдена первообразная функции F(x) для подынтегральной функции 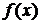 .
.
Методы вычислений определенного интеграла: непосредственное интегрирование; интегрирование подстановкой; интегрирование по частям.
Интегрирование по частям
Теорема. Если функции 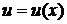 и
и 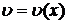 имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке 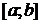 , то имеет место формула
, то имеет место формула
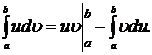 | (5.3.1) |
Формула (2) называется формулой интегрирования по частям для определенного интеграла
Интегрирование методом подстановки
Пусть для вычисления интеграла 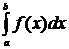 от непрерывной функции f(x) сделана подстановка
от непрерывной функции f(x) сделана подстановка 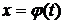 .
.
Теорема. Если:
1. Функция 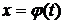 и ее производная
и ее производная 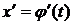 непрерывны при
непрерывны при 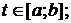
2. Множеством значений функции 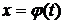 при
при 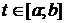 является отрезок
является отрезок 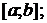
3. 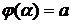 и
и 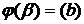 ,
,
то
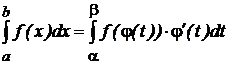 . . | (2.5.1) |
Формула (5.2.1) называется формулой замены переменной в определенном интеграле.
Отметим, что: 1. При вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется; 2. Часто вместо подстановки 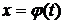 применяют подстановку t = g(x);
применяют подстановку t = g(x);
Непосредственное интегрирование представляет собой метод, основанный на свойствах интеграла.
Приложение определенного интеграла: формулы площадей плоских фигур, длины кривой, объема ткл вращения.
Площади фигур в декартовой системе координат
Площадь фигуры, ограниченной кривыми 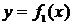 и
и 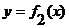 , прямыми х = а и х = b (при
, прямыми х = а и х = b (при 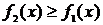 ) можно найти по формуле
) можно найти по формуле 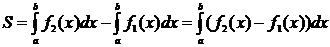 .
.
Если плоская фигура имеет «сложную» форму, то прямыми, параллельными оси Оу, ее следует разбить на части так, чтобы можно было бы применить уже известные формулы.
Если криволинейная трапеция ограничена прямыми у = с и у = d, осью Оу и непрерывной кривой 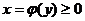 , то ее площадь находится по формуле
, то ее площадь находится по формуле 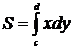 .
.
