Квадратная матрица называется невырожденной или неособенной, если ее определитель отличен от нуля. В противном случае квадратная матрица называется вырожденной или особенной.
Теорема существования и единственности. Обратная матрица существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.
Алгоритм нахождения обратной матрицы:
1.Находим определитель исходной матрицы. Если 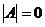 , то матрица вырожденная и для нее обратной матрицы не существует. Если
, то матрица вырожденная и для нее обратной матрицы не существует. Если 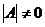 , то матрица невырожденная и для нее можно найти обратную матрицу.
, то матрица невырожденная и для нее можно найти обратную матрицу.
Находим алгебраические дополнения всех элементов матрицы.
3. Составляем из полученных алгебраических дополнений так называемую союзную матрицу 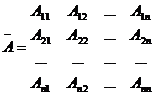
4. Обратную матрицу находим по формуле: A-1= 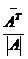 .
.
Решение систем линейных алгебраических уравнений: методом Гаусса; по правилам Крамера; с помощью обратной матрицы.
Рассмотрим произвольную систему m линейных алгебраических уравнений (СЛАУ) с n - неизвестными:
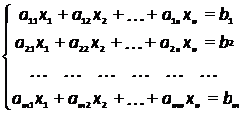 (3.7)
(3.7)
Решением системы (3.7) называется совокупность значений неизвестных при подстановке которых все уравнения системы обращаются в тождества. Система, имеющая хотя бы одно решение, называется совместной, а система не имеющая ни одного решения, называется несовместной. Система, имеющая единственной решение, называется определенной, система, имеющая более одного решения, - неопределенной.
Рассмотрим матрицу A, составленную из коэффициентов при неизвестных системы (3.7) и матрицу B, получаемую из A добавлением столбца свободных членов:
 и
и 
Матрицу A назовем матрицей системы (3.7), а матрицу B назовем расширенной матрицей системы (3.7). Очевидно, что r (A) £ r (B), так как каждый минор матрицы A будет минором матрицы B, но не наоборот.
I. Метод Крамера.
Метод Крамера рассматривается для систем из n уравнений с n неизвестными, т.е. для систем вида: 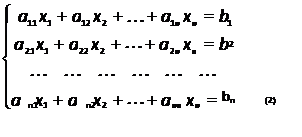
Пусть определитель основной матрицы такой системы отличен от нуля:
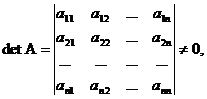
тогда неизвестные x1, x2,…, xn можно найти по формулам Крамера:
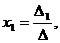
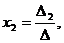 …,
…, 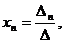
где 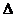 - определитель основной матрицы системы,
- определитель основной матрицы системы, 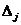 (j=1,n) – определитель, получаемый из
(j=1,n) – определитель, получаемый из 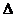 заменой j-го столбца столбцом свободных членов.
заменой j-го столбца столбцом свободных членов.
Если определитель 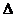 =0, то либо система (2) не имеет решения, либо имеет множество решений. Если все
=0, то либо система (2) не имеет решения, либо имеет множество решений. Если все 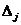 (j=1,n) равны нулю, то система совместна, но неопределенна, если хотя бы одно
(j=1,n) равны нулю, то система совместна, но неопределенна, если хотя бы одно 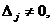 то система (2) не совместна.
то система (2) не совместна.
II. Метод Гаусса.
Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса, состоящий в последовательном исключении неизвестных.
Пусть задана система линейных алгебраических уравнений
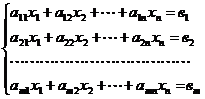 (3.8)
(3.8)
Будем производить над системой следующие элементарные преобразования:
Вычеркивание уравнения вида
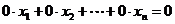
Так как этому уравнению удовлетворяют любые значения неизвестных. Если мы припишем такое уравнение к некоторой системе или, наоборот, вычеркнем его из системы, то новая система будет равносильна первоначальной.
Прибавление к одному уравнению другого уравнения, умноженного на произвольное число.
