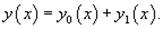Решение Д.У. типа F(y,y’,y’’)

^{3. Рассмотрим уравнение вида 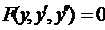, т.е. уравнение, в запись которого явно не входит независимая переменная. Такое уравнение можно решить, введя новую неизвестную функцию 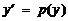. Сделав замену переменной и учитывая, чт}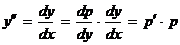

^{где 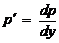, получим уравнение первого порядка относительно новой искомой функции p(y) и новой независимой переменной y, т.е. понизим порядок исходного уравнения на одну единицу. Если удастся отыскать общее решение полученного уравнения первого порядка, т.е. 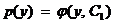, то для нахождения общего решения исходного уравнения необходимо решить следующее дифференциальное уравнение первого порядка 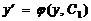. Это уравнение является уравнением первого порядка с разделяющимися переменным}

13Линейные однородные д.у. высших порядков: Для линейного однородного дифференциального уравнения n-го порядкаy⁽ⁿ⁾ + a₁(x) y^(n-1) + ... + a_n-1 (x) y' + a_n(x) y = 0, где y = y(x) — неизвестная функция, a₁(x), a₂(x), ..., a_n-1(x), a_n(x) — известные, непрерывные, справедливо:
1) существуют n линейно независимых решений уравнения
y₁(x), y₂(x), ..., y_n(x);
2) при любых значениях констант c₁,0 c₂, ..., c_n функция
y(x)=c₁y₁(x)+ c₂y₂(x)+...+c_ny_n(x) является решением уравнения;
3) для любых начальных значений x₀, y₀, y_0,1, ..., y_0,n-1 существуют такие значения c*₁, c*_n, ..., c*_n, что решение
y*(x)=c*₁y₁(x)+c*₂y₂(x)+...+c*_ny_n(x) удовлетворяет при x=x₀ начальным условиям
y*(x₀)=y₀, (y*)'(x₀)=y_0,1 , ...,(y*)^(n-1)(x₀)=y_0,n-1.

Выражение y(x)= c₁ y₁(x) + c₂ y₂(x) + ... + c_n y_n(x) называется общим решением линейного однородного дифференциального уравнения n-го порядка.

Совокупность n линейно независимых решений линейного однородного дифференциального уравнения n-го порядка y₁(x), y₂(x), ..., y_n(x) называется фундаментальной системой решений уравнения.

Если в уравнении yⁿ=f(x,y,y’,…y^n-1) функция f и ее частные производные y, y', y''… непрерывны в некоторой области содержащей значения x=x₀, y=y₀, y’=y’₀, …, то существует и при том единственное решение y=y(x) уравнения удовлетворяющего условию y(x₀)=y₀, y’(x₀)=y’₀… , которые называются начальными условиями.

Общим решением ДУ n-ого порядка называется функция y=φ(x, C1, C2…), зависящая от n- произвольных постоянных и такая, что она удовлетворяет ДУ при любом значении постоянных с, с1, с2… , а при заданных начальных условиях y(x₀)=y₀, y’(x₀)=y’₀…

14 нахождение общего решения лин.однородных д.у.

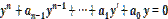
Характеристическое уравнение

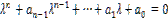
Где -решение характеристического уравнения

Общее решение

Все корни характеристического уравнения различные, тогда

+…

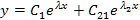Если среди корней есть пары комплексно-сопряженных корней, например λ1=α+iβ и λ2=α-iβ, решение можно записать в виде

+ +…

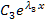Линейные неоднородные д.у.

Линейное неоднородное уравнение данного типа имеет вид:

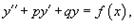
где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:

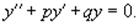
Теорема: Общее решение неоднородного уравнения является суммой общего решения y₀(x) соответствуюшего однородного уравнения и частного решения y₁(x) неоднородного уравнения: