Выпуклость, вогнутость графика функции; достаточные условия.

Функция f ( x ) называется выпуклой на интервале ( a, b ), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f ( x ) в любой точке ( x₀, f ( x₀ ) ), x₀ ( a, b ).

Функция f ( x ) называется вогнутой на интервале ( a, b ), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f ( x ) в любой точке ( x₀, f ( x₀ ) ), x₀ 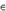( a, b ).

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если f '' ( x ) > 0 для любого x 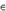( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );

если f '' ( x ) < 0 для любого x 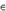( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .

Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x₀ существует вторая производная f '' ( x₀ ), то f '' ( x₀ ) = 0.

Наименьшее и наибольшее значения непрерывной на отрезке функции.

Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке

Говорят, что функция 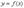, определенная на промежутке Х, достигает на нем своего наибольшего (наименьшего) значения, если существует точка а, принадлежащая этому промежутку, такая, что для всех х из Х выполняется неравенство .

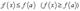Функция, непрерывная на отрезке, достигает на нем своего наибольшего и наименьшего значений.

Наибольшее значение М и наименьшее значение m непрерывной функции могут достигаться как внутри отрезка, так и на его концах. Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка является точкой экстремума.

Применение дифференциала в приближенных вычислениях.

Как уже известно, приращение ∆у функции у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство

∆у≈dy, (24.3)

причем это равенство тем точнее, чем меньше ∆х.

Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.

Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (24.3) широко применяется в вычислительной практике.

Дифференциалы высших порядков.

Дифференциал высшего порядка функции одной переменной

Для функции, зависящей от одной переменной второй и третий дифференциалы выглядят так:

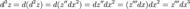
Отсюда можно вывести общий вид дифференциала n-го порядка от функции :

При вычислении дифференциалов высших порядков очень важно, что есть произвольное и не зависящее от , которое при дифференцировании по следует рассматривать как постоянный множитель.

Дифференциал высшего порядка функции нескольких переменных

Если функция 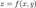имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так: .