Бесконечно малые величины и их св-ва

Опр. Функция f(x) называется бесконечно малой при х®а, где а может быть числом или одной из величин ¥, +¥ или -¥, если 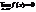.Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.Пример. Функция f(x) = xⁿ является бесконечно малой при х®0 и не является бесконечно малой при х®1, т.к. 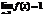.Теорема. Для того, чтобы функция f(x) при х®а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие f(x) = A + a(x),где a(х) – бесконечно малая при х ® а (a(х)®0 при х ® а).

Используя понятие бесконечно малых функций, приведем доказательство некоторых теорем о пределах

.Доказательство теоремы 2. Представим f(x) = A + a(x), g(x) = B + b(x), где 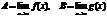, тогдаf(x) ± g(x) = (A + B) + a(x) + b(x)

A + B = const, a(х) + b(х) – бесконечно малая, значит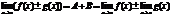

Теорема доказана.Доказательство теоремы 3. Представим f(x) = A + a(x), g(x) = B + b(x), где 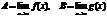, тогда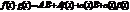

A×B = const, a(х) и b(х) – бесконечно малые, значит 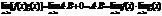Теорема доказана.

Числовая последовательность и ее предел.

Числ послед-ть– функция вида y = f(x), x Î N,где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f(n)или y₁, y₂,…, y_n,…. Значения y₁, y₂, y₃,…называют соответственно первым, вторым, третьим, … членами последовательности.

Например, для функции y = n² можно записать:

y₁ = 1² = 1;

y₂ = 2² = 4;

y₃ = 3² = 9;…y_n = n²;…

^.

^{Строгое определение предела формулируется следующим образом:}

^{Если существует такое число A, что для любого (сколь угодно малого) положительного числа e найдется такое натуральное N (вообще говоря, зависящее от e), что для всех n і N будет выполнено неравенство |a}_n ^{– A| < e, то говорят, что последовательность{a}_n^{}сходится и A – ее предел.}

^{Обозначается это так: .}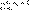

^{В противном случае последовательность называется расходящейся}

Й, замечательный предел.

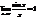Доказательство: докажем для 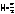справедливость неравенства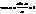

В силу четности входящих в неравенство ф-ий, докажем это неравенство на промежутке 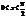Из рисунка видно, что площадь кругового сектора

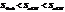
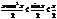, так как х>0, то ,

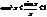2. следовательно, что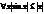

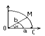
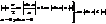
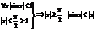
1. Покажем, что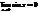

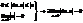
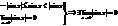
2. Докажем, что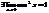

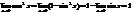
3. Последнее утверждение:

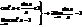
Второй замечательный предел

lim(n®¥)(1+1/n)^n=e Док-во:

x®+¥ n x:n=[x] => n£x<n+1 => 1/(n+1)<1/x<1/n

Посколько при ув-нии основания и степени у показательной ф-ции, ф-ция возрастает, то можно записать новое неравенство (1/(n+1))^n£(1+1/n)^x£ (1+1/n)^(n+1) (4)

Рассмотрим пос-ти стоящие справа и слева. Покажем что их предел число е. Заметим (х®+¥, n®¥)

lim(n®¥)(1+1/(n+1))=lim(n®¥)(1+1/(n+1))^n+1-1= lim(n®¥)(1+1/(n+1))^n+1*lim(n®¥)1/(1+1/(n+1))=e

lim(n®¥)(1+1/n)^n+1= lim(n®¥)(1+1/n)^n* lim(n®¥)(1+1/n)=e*1=e

10.3.Сравнение бесконечно малых. Эквивалентные бесконечно малые.

Пусть a(х), b(х) и g(х) – бесконечно малые функции при х ® а. Будем обозначать эти функции a, b и g соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.Например, функция f(x) = x¹⁰ стремится к нулю быстрее, чем функция f(x) = x.Опр. Если 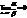, то функция a называется бесконечно малой более высокого порядка, чем функция b.

Опр. Если 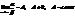, то a и b называются бесконечно малыми одного порядка.Опр. Если 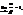то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.Пример. Сравним бесконечно малые при х®0 функции f(x) = x¹⁰ и f(x) = x. 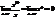т.е. функция f(x) = x¹⁰ – бесконечно малая более высокого порядка, чем f(x) = x. Опр. Бесконечно малая функция a называется бесконечно малой порядка kотносительно бесконечно малой функции b, если предел 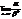конечен и отличен от нуля.Однако следует отметить, что не все бесконечно малые функции можно сравнивать между собой. Например, если отношение 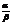не имеет предела, то функции несравнимы.

Свойства эквивалентных бесконечно малых.1) a ~ a, 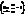2) Если a ~ b и b ~ g, то a ~ g, 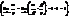3) Если a ~ b, то b ~ a,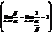

4) Если a ~ a₁ и b ~ b₁ и 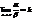, то и 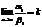или .

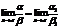Следствие: а) если a ~ a₁ и 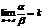, то и 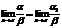б) если b ~ b₁ и 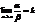, то 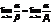Свойство 4 особенно важно на практике, т.к. оно фактически означает, что предел отношения бесконечно малых не меняется при замене их на эквивалентные бесконечно малые. Этот факт дает возможность при нахождении пределов заменять бесконечно малые на эквивалентные им функции, что может сильно упростить вычисление пределов.

12.3. Непрерывность функции в точке. Действия над непрерыв функциями

x=x₀+Dx, Dx=x-x₀

Dy=f(x₀+Dx)-f(x₀)

Ф-ция y=f(x) наз. непрерывной в точке x₀, если она определена в окрестности этой точки, а limDy=0. (бесконеч.малая. приращению аргумента соответствует б.м. приращению ф-ции).

limDy=lim[f(x)-f(x₀)]=limf(x)-limf(x₀)=0, то

limf(x)=limf(x₀)

x®x₀

Ф-ция непрерывна в точке х₀, если ее предел = значению этой ф-ции в точке х₀

Ф-ция явл. непрерывной на интервале, если она непрерывна в каждой его точке.