Изолированные особые точки, их классификация.

Основные понятия и определения:

Нулем аналитической функции f(z) называется точка “a”, для которой f(a)=0.

Нулем порядка “n” функции f(z) называется точка «а», если 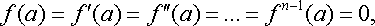но fn(a)¹0.

Особая точка «a» называется изолированной особой точкой функции f(z), если существует окрестность этой точки, в которой нет особых точек, кроме «a».

Изолированные особые точки бывают трех типов: .

1 устранимые особые точки;

2 полюсы;

3 существенно особые точки.

Тип особой точки может быть определен исходя из поведения данной функции в найденной особой точке, а также из вида ряда Лорана, полученного для функции в окрестности найденной особой точки.

Определение типа особой точки по поведению функции в ней.

1.Устранимые особые точки.

Изолированная особая точка a функции f(z) называется устранимой, если существует конечный предел .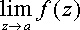

2.Полюсы.

Изолированная особая точка a функции f(z) называется полюсом, если .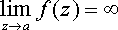

3.Существенно особые точки.

Изолированная особая точка a функции f(z) называется существенно особой точкой, если не существует ни конечный, ни бесконечный .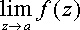

Между нулями и полюсами функции имеет место следующая связь.

Для того, чтобы точка a была полюсом порядка n функции f(Z), необходимо и достаточно, чтобы эта точка была нулем порядка n для функции .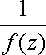

Если n=1 полюс называется простым.

Определение:Изолированная особая точка однозначного характера называется :

а) устранимой, если главная часть разложения отсутствует;

б) полюсом, если главная часть содержит конечное число членов;

в) существенно особой точкой, если главная часть содержит бесконечное число членов.

а) Таким образом, в окрестности устранимой особой точки разложение имеет вид :

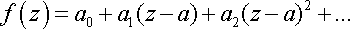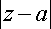, 0< <R,

оно выражает функцию во всех точках круга |z-a| <R, кроме центра z=a.

В центре z=a равенство неверно, т.к. функция при z=a имеет разрыв, а правая часть непрерывна. Если в центре значение функции изменить, приняв его равным значению правой части, то разрыв будет устранен- отсюда и название – устранимый.

б) В окрестности полюса порядка m разложение в ряд Лорана имеет вид:

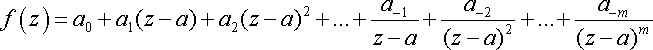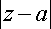; 0< <R.

в) В окрестности простого полюса

,

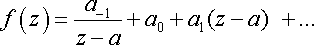
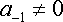
Вычеты и формулы для их вычисления.

Вычетом аналитической функции f(z) в изолированной особой точке z₀ называется комплексное число, равное значению интеграла 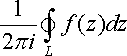, взятого в положительном направлении по окружности L с центром в точке z₀, лежащей в области аналитичности функции f(z) (т.е. в кольце 0<|z-z0|<R).

Обозначается вычет функции f(z) в изолированной особой точке z₀ символом Res f(z₀) или Res (f(z); z₀). Таким образом,

Res f(z₀)= 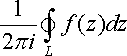. (22.15.1)

Если в формуле ( 22.15.1 ) положить n=-1, то получим:

C_-1=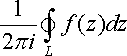

или Res f(z₀)= C_-1 ,

т.е. вычет функции f(z) относительно особой точки z₀ равен коэффициенту при первом члене с отрицательным показателем в разложении функции f(z) в ряд Лорана.

Вычисление вычетов.

Правильные или устранимые особые точки. Очевидно, если z=z₀ есть правильная или устранимая особая точка функции f(z), то Res f(z₀)=0 (в разложении Лорана в этих случаях отсутствует главная часть, поэтому c-1=0).

Полюс. Пусть точка z₀ является простым полюсом функции f(z). Тогда ряд Лорана для функции f(z) в окрестности точки z₀ имеет вид:

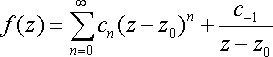
Отсюда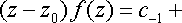

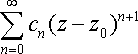
Поэтому, переходя в этом равенстве к пределу при z --z₀, получаем

Res f(z0)=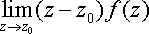

(22.15.5)

Существенно особая точка. Если точка z₀ - существенно особая точка функции f(z), то для вычисления вычета функции в этой точке обычно непосредственно определяют коэффициент c-1 в разложении функции в ряд Лорана.