Уравнение плоскости, проходящей через три заданные точки
Если относительно некоторой прямоугольной системы координат в пространстве даны точки M1(x1; y1; z1), M2(x2; y2; z2), M3(x3; y3; z3), принадлежащие некоторой плоскости, то уравнение этой плоскости имеет вид:
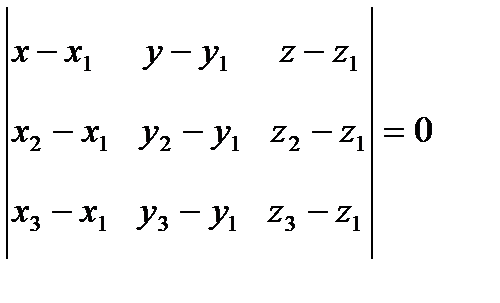 .
.
Уравнение плоскости в «отрезках»
Если некоторая плоскость отсекает на осях координат отрезки: а– на оси 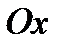 , b – на оси
, b – на оси 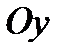 , с – на оси
, с – на оси 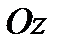 , то уравнение этой плоскости имеет вид:
, то уравнение этой плоскости имеет вид:
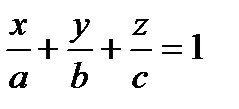 .
.
Уравнение плоскости, проходящей через заданную точку перпендикулярно данному вектору
Пусть относительно некоторой прямоугольной системы координат плоскость проходит через точку M0(x0; y0; z0) перпендикулярно вектору 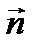 (A; B; C). Уравнение этой плоскости будет иметь вид:
(A; B; C). Уравнение этой плоскости будет иметь вид:
A(x-x0)+B(y-y0)+C(z-z0)=0.
Общее уравнение плоскости. Условие параллельности вектора некоторой плоскости
Какими бы способами ни была задана плоскость, ее уравнение можно привести к виду:
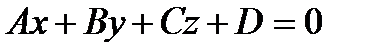 .
.
Это уравнение называется общим уравнением плоскости.
Если плоскость задана относительно прямоугольной системы координат, то коэффициенты A, B, C этого уравнения служат координатами вектора нормали к данной плоскости: 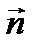 (A; B; C).
(A; B; C).
Вектор 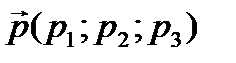 параллелен плоскости, определяемой уравнением
параллелен плоскости, определяемой уравнением 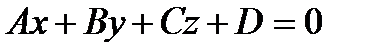 , тогда и только тогда, когда выполняется условие:
, тогда и только тогда, когда выполняется условие:
Ap1+Bp2+Cp3=0.
Расстояние от точки до плоскости
Расстояние от точки M0(x0; y0; z0) до плоскости, определяемой в прямоугольной системе координат общим уравнением 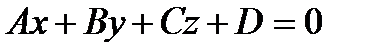 , находится с помощью формулы:
, находится с помощью формулы:
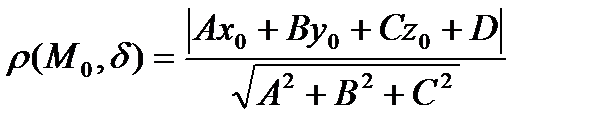 .
.
Прямая в пространстве
Вектор, параллельный прямой, называется направляющим вектором прямой.
Различные способы задания прямой
Уравнение прямой, проходящей через данную точку параллельно данному вектору.
Прямая, проходящая через точку M0(x0; y0; z0) параллельно направляющему вектору 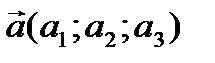 , определяется или параметрическими уравнениями:
, определяется или параметрическими уравнениями:
x = x0+ 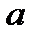 1t,
1t,
y = y0+ 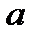 2t,
2t,
z = z0+ 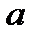 3t,
3t,
где t – параметр, принимающий произвольные значения, или каноническими уравнениями вида:
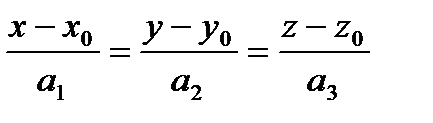 .
.
(В этом уравнении отношения рассматриваются как пропорция, а не как дроби).
Прямая как линия пересечения двух плоскостей
Прямая как линия пересечения двух плоскостей определяется системой уравнений этих плоскостей:
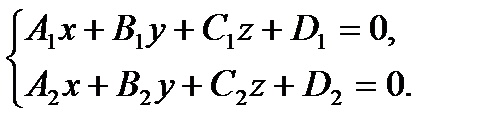
Координаты  1,
1,  2,
2, 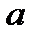 3 направляющего вектора
3 направляющего вектора 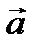 этой прямой равны:
этой прямой равны:
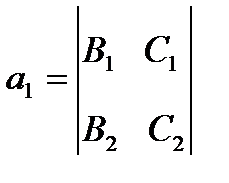 ,
, 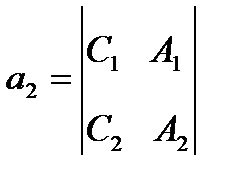 ,
, 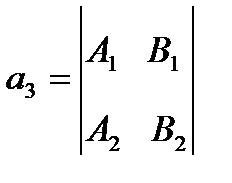 ,
,
т.е. 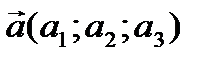 .
.
Уравнения прямой, проходящей через две точки
Канонические уравнения прямой, проходящей через две данные точки M1(x1; y1; z1), M2(x2; y2; z2), имеют вид:
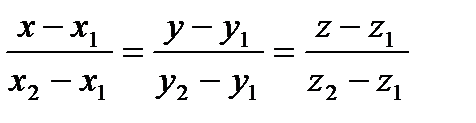 .
.
15 Способы задания прямой в пространстве.
5.3. Прямая в пространстве
Вектор, параллельный прямой, называется направляющим вектором прямой.
Различные способы задания прямой
Уравнение прямой, проходящей через данную точку параллельно данному вектору.
Прямая, проходящая через точку M0(x0; y0; z0) параллельно направляющему вектору 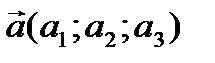 , определяется или параметрическими уравнениями:
, определяется или параметрическими уравнениями:
x = x0+ 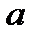 1t,
1t,
y = y0+ 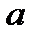 2t,
2t,
z = z0+ 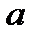 3t,
3t,
где t – параметр, принимающий произвольные значения, или каноническими уравнениями вида:
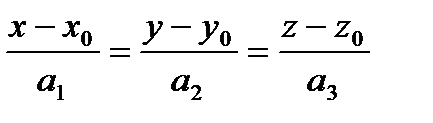 .
.
(В этом уравнении отношения рассматриваются как пропорция, а не как дроби).
