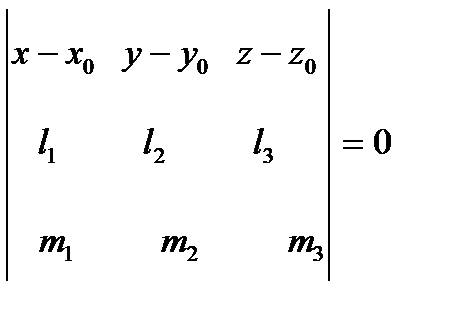Смешанное произведение трех векторов, его геометрический смысл.
Смешанное произведение векторов
Смешанным произведением трех векторов 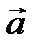 ,
, 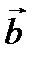 ,
, 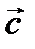 называется число, равное векторному произведению
называется число, равное векторному произведению 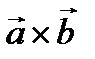 , умноженному скалярно на вектор
, умноженному скалярно на вектор 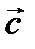 , то есть
, то есть 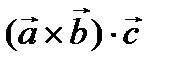 .
.
Модуль смешанного произведения трех векторов равен объему параллелепипеда, построенного на векторах 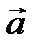 ,
, 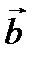 ,
, 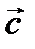 .
.
Смешанное произведение не меняется при круговой перестановке сомножителей: 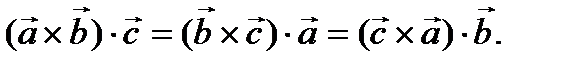
Смешанное произведение меняет знак на противоположный при всякой перестановке, изменяющей последовательность сомножителей:
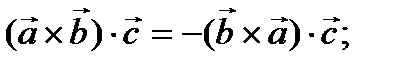
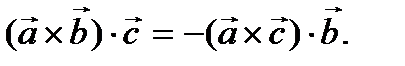
Смешанное произведение равно нулю тогда и только тогда, когда векторы 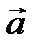 ,
, 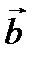 ,
, 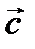 компланарны.
компланарны.
Вычисление смешанного произведения векторов
Если векторы 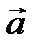 (
( 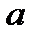 1;
1; 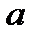 2;
2; 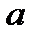 3),
3), 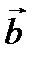 (b1; b2; b3),
(b1; b2; b3), 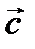 (c1; c2; c3) заданы относительно прямоугольной системы координат, то смешанное произведение векторов вычисляется:
(c1; c2; c3) заданы относительно прямоугольной системы координат, то смешанное произведение векторов вычисляется:
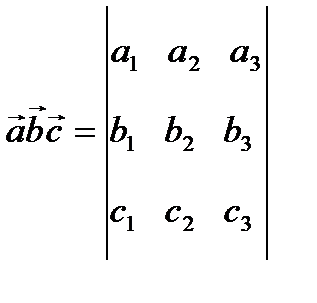 .
.
12 Способы задания прямой на плоскости. Расстояние от точки до прямой.
Прямая на плоскости
Всякая прямая относительно прямоугольной системы координат на плоскости определяется уравнением первой степени, и обратно, всякое уравнение первой степени относительно координат 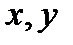 описывает некоторою прямую на плоскости.
описывает некоторою прямую на плоскости.
Любой ненулевой вектор, параллельный данной прямой, называется её направляющим вектором.
Различные способы задания прямой
Уравнение прямой, заданной точкой и направляющим вектором
Пусть дана некоторая прямая, которая проходит через точку 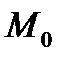 с известными координатами
с известными координатами 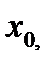 ,
, 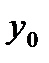 параллельно направляющему вектору
параллельно направляющему вектору 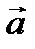 , координаты которого также известны и равны (
, координаты которого также известны и равны ( 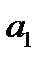 ,
, 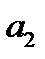 ).
).
Уравнение этой прямой можно записать в виде:
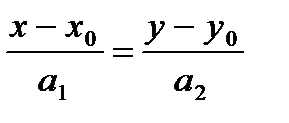 .
.
Это равенство называется каноническим уравнением прямой.
Параметрические уравнения прямой
Существует ещё один вид уравнения прямой, проходящей через данную точку 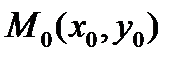 и имеющей данный направляющий вектор
и имеющей данный направляющий вектор 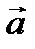
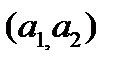 :
: 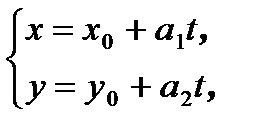
где 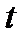 - параметр, принимающий все действительные значения.
- параметр, принимающий все действительные значения.
Этот вид называется параметрическими уравнениями прямой.
Уравнение прямой, проходящей через две заданные точки
Пусть некоторая прямая проходит через две точки с известными координатами: 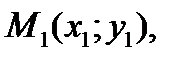
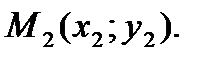 . Уравнение этой прямой имеет вид:
. Уравнение этой прямой имеет вид: 
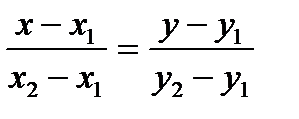 .
.
Уравнение прямой “в отрезках по осям”
Пусть прямая отсекает на оси 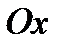 отрезок величины
отрезок величины 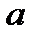 , на оси
, на оси 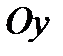 – отрезок
– отрезок 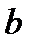 . В этом случае уравнение прямой будет иметь вид:
. В этом случае уравнение прямой будет иметь вид:
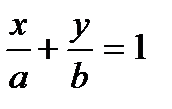 .
.
Расстояние от точки до прямой
Расстояние от точки 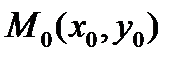 до прямой
до прямой 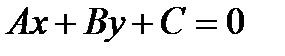 вычисляется по формуле
вычисляется по формуле
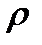 (
( 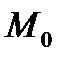 ,
, 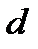 )=
)= 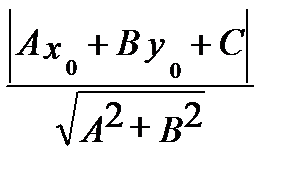 .
.
Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых
Тангенс угла между прямыми, уравнения которых относительно прямоугольной системы координат заданы в виде 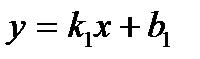 и
и 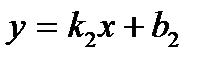 , вычисляется по формуле
, вычисляется по формуле
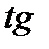
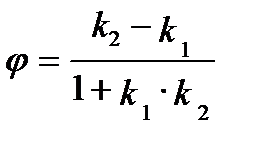 ,
,
причём угол принято отсчитывать против часовой стрелки от первой прямой ко второй.
Необходимое и достаточное условие параллельности заданных прямых выражается равенством 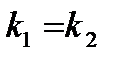 , а условие перпендикулярности
, а условие перпендикулярности 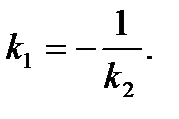
14 Способы задания плоскости в пространстве. Расстояние от точки до плоскости.
Всякая плоскость относительно некоторой прямоугольной системы координат в пространстве определяется уравнением первой степени и обратно: каждое уравнение первой степени определяет плоскость.
Различные способы задания плоскости
Уравнение плоскости, проходящей через заданную точку параллельно двум неколлинеарным векторам
Пусть относительно некоторой прямоугольной системы координат в пространстве дана точка M0(x0; y0; z0) некоторой плоскости и два неколлинеарных вектора 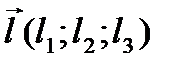 ,
, 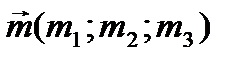 , параллельные этой плоскости.
, параллельные этой плоскости.
Тогда уравнение плоскости можно записать так: