Способы построения обратной матрицы.

Понятие. Отметим, что для любого ненулевого вещественного числа 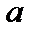определено понятие обратного числа 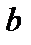– такого, что 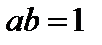. По аналогии, для квадратной матрицы порядка 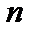рассмотрим понятие обратной матрицы.

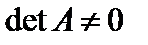Будем говорить, что матрица – невырожденная, если ее определитель , и вырожденная – в противном случае ( ).

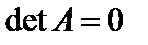Присоединенной матрицей для 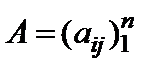называется матрица

,

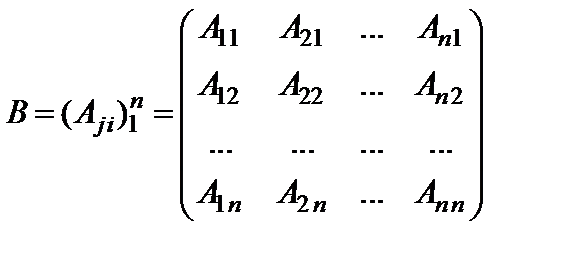где 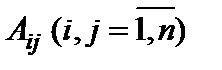– алгебраическое дополнение элемента 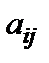матрицы . Отметим, что алгебраические дополнения элементов 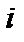-ой строки 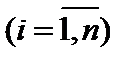матрицы находятся в 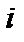-ом столбце матрицы .

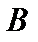Лемма Для рассматриваемых матриц и 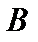имеет место равенство

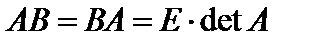, (10)

где 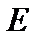– единичная матрица порядка .

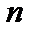Если для матрицы существует такая матрица 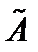, что

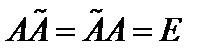, (11)

где 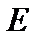– единичная матрица, то матрица 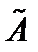называется обратной для матрицы .

Обратную матрицу для матрицы обозначают 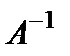и тогда равенство (11) принимает вид

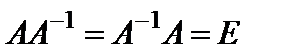. (12)

Из (12) непосредственно вытекает, что для существования обратнойматрицы необходимо, чтобы исходная матрица была квадратной, причем обе матрицы и 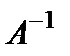имеют одинаковый порядок. Таким образом, понятие обратной матрицы имеет смысл только для квадратной.

Построениематрицы.К элементарным преобразованиям матрицы относятся:

1) умножение столбца (строки) матрицы на число, не равное нулю;

2) прибавление к одному столбцу (строке) матрицы другого столбца (строки), умноженного на произвольное число, не равное нулю;

3) перестановка местами двух столбцов (строк) матрицы.

Если матрица 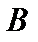получена из матрицы с помощью элементарных преобразований, то будем говорить «матрица А эквивалента матрице В»и писать .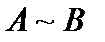

Очевидно, что если 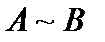и , то .

Утверждение 2. Любую невырожденную матрицу можно преобразовать в единичную с помощью элементарных преобразований только столбцов (или только строк).

Для построения обратной матрицы 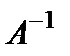удобно записывать матрицы и 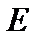через черту одна под другой, если преобразуются столбцы, или рядом, если преобразуются строки. Матрица, полученная на месте единичной после того, как матрица А преобразуется в единичную, и будет матрицей .

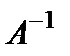12. Ранг матрицы и его свойства. Рассмотрим прямоугольную матрицу вида:

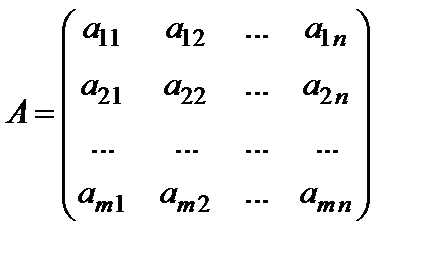. (1)

Рангом матрицы назовем наибольший порядок не равного нулю ее минора (ранг нулевой матрицы 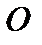считаем равным нулю).

Для ранга матрицы используют следующие обозначения: 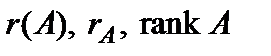или просто 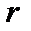, когда ясно, о какой матрице идет речь.

Из определения ранга матрицы и свойств определителя из §3 вытекают следующие свойства ранга матрицы.

1) Для матрицы 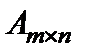справедливо 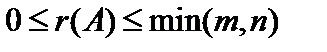, где 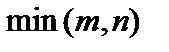– меньшее из чисел 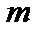и .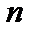

2) Равенство 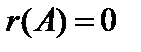справедливо тогда и только тогда, когда – нулевая матрица .

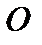3) Для квадратной матрицы порядка 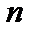имеем 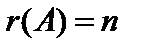тогда и только тогда, когда невырожденная матрица.

4) Для любой матрицы справедливо .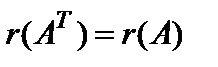

5) Ранг матрицы, полученной из исходной вычеркиванием какого-нибудь ее столбца (или строки), равен рангу исходной матрицы или меньше его на единицу.

6) Ранг матрицы, полученной из данной матрицы в результате приписывания к ней произвольного столбца (или строки), равен рангу исходной матрицы или больше его на единицу.

7) Если к матрице дописать или вычеркнуть нулевой столбец (нулевую строку), ранг полученной матрицы равен рангу исходной.

Из формул Лапласа (3.4) и (3.5) заключаем: если среди миноров порядка 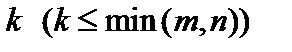матрицы размера 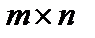есть не равные нулю, а все миноры 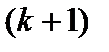-го порядка равны нулю, то .

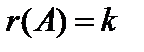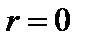В связи со сказанным выше, ранг матрицы можно найти так. Если все миноры первого порядка, т.е. элементы матрицы , равны нулю, то . В случае, когда есть хотя бы один ненулевой элемент матрицы, рассмотрим миноры второго порядка, включающие в себя этот элемент. Если все они равны нулю, то 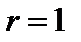. При наличии хотя бы одного ненулевого минора второго порядка рассмотрим миноры третьего порядка и т.д. Этот процесс продолжим до тех пор, покане станет ясно, что все миноры порядка 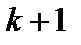равны нулю или уже не существуют. Тогда получаем, что .

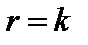13. Основные понятия СЛАУ. Системой m линейных алгебраических уравнений с 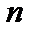неизвестными 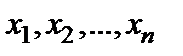назовем систему вида

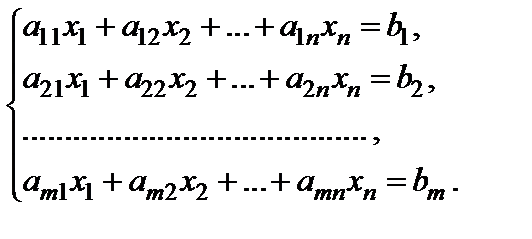(1)

Числа 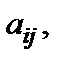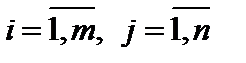, называются коэффициентами системы, а числа 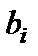, , 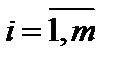– свободными членами (правыми частями).

Дальше в этой главе выражение «алгебраических» для краткости опускаем.

Если все 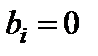, , 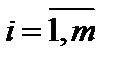то система называется однородной; если хотябы один из свободных членов ненулевой, то система (1) называетсянеоднородной.

Решением системы (1) называют любую упорядоченную совокупность 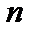чисел 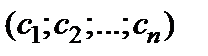, которые при подстановке в каждое уравнение системы (1) на место соответствующих неизвестных обращают его в тождество. Систему (1) называют совместной, если она имеет хотя бы одно решение, в противном случае – несовместной. Совместная система, имеющая только одно решение (больше чем одно решение), называется определенной (неопределенной).

Решить систему (1) – означает выяснить совместная она или нет, и, если совместная, то найти все ее решения.

Например, если в системе (1) 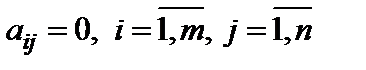, то: 1) она несовместна, если есть хотя бы одно из 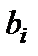не равно нулю; 2) система (1) имеет бесконечное множество решений при 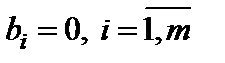, и, более того, любая упорядоченная совокупность n чисел 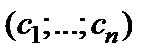будет ее решением.

Систему (1) удобно записывать в матричной форме. Матрица

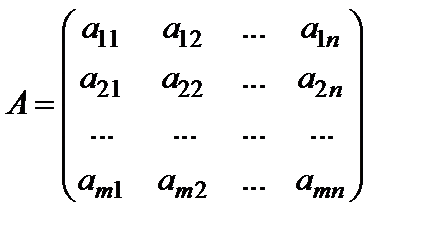, (2)

состоящая из коэффициентов системы (1), называется матрицей этой системы. Введем также матрицу-столбец неизвестных x и матрицу-столбец свободных членов b:

.

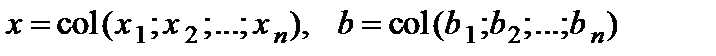Из определения произведения матриц следует, что левую часть системы (1) можно представить как произведение матрицы А на матрицу-столбец x, а ее правая часть есть матрица-столбец b. Поэтому получаем матричную запись системы (1):

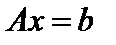. (3)

Если 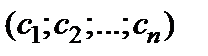– решение системы (1), то матрица столбец 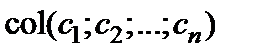удовлетворяет уравнению (3) и называется вектор-решением системы (1).

Используя матрицы-столбцы коэффициентов системы (1), ее можно записать также в виде:

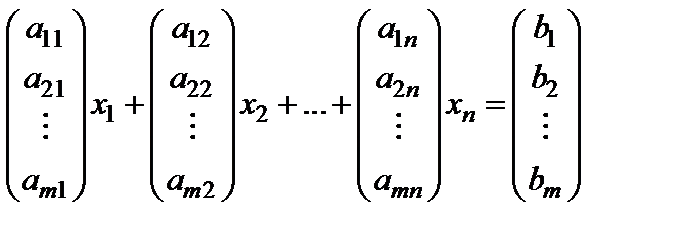. (4)

Две системы называют эквивалентными или равнозначными, еслиони имеют одно и то же множество решений. Считаем, что всякие две несовместные системы с одинаковым числом неизвестных – эквивалентны.

15.Матритичный методСЛАУ. Исследование систем линейных уравнений. Часто в математических исследованиях и практических приложениях нужно знать, является ли совместной система (9.1), а если это так, то сколько решений она имеет. Ответ на первую часть поставленного вопроса содержится в теореме Кронекера-Капелли. В частности, невырожденную систему (9.10) можно решить по правилу Крамера и, значит, такая система имеет единственное решение.

В общем случае при исследовании совместной системы используют сформулированные ниже утверждения.

Утверждение 1. Если ранг матрицы совместной системы равен количеству неизвестных, то система имеет единственное решение.

Доказательство.Пусть указанная система совместна. Тогда на основании теоремы 6.1 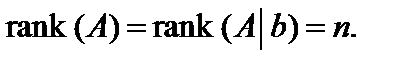Поэтому существует минор, который будет базисным одновременно для матриц А и 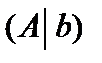. Каждый небазисный столбец матрицы ( 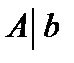) есть линейная комбинация ее n базисных столбцов. Поэтому система (6.1) эквивалентна системе тех n уравнений первоначальной системы, в которых коэффициенты при неизвестных образуют базисный минор. Последняя система является невырожденной системой n уравнений с n неизвестными и имеет единственное решение, которое можно найти по правилу Крамера. □

Утверждение 2. Если ранг матрицы совместной системы меньше количества неизвестных, то система имеет бесчисленное множество решений

16. Метод Гаусса. Распространенным точным методом решения систем (1) является метод Гаусса. Суть метода состоит в том, что посредством элементарных преобразований система (1) приводится к треугольной или трапециевидной форме, из которой все решения системы получаются непосредственно.

Рассмотрим систему (9.1), где коэффициент 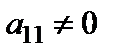. Если бы было 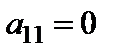, то на первое место в системе (1) поставили бы уравнение, в котором коэффициент при 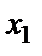отличен от нуля. Пусть далее в i-ом уравнении 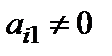. Умножим обе части первого уравнения на 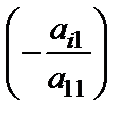и сложим его с i-ым уравнением. В результате получим уравнение

,

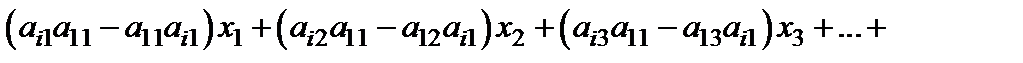
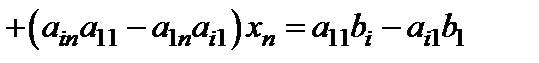где коэффициент при 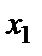равен нулю.

Преобразуем таким образом все уравнения системы, в которых 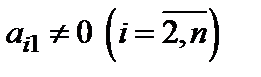и, преобразуя соответствующие коэффициенты, получим систему

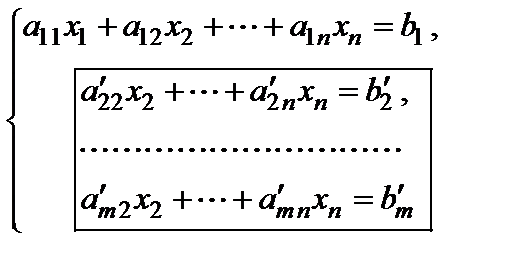(3)

в которой рамкой выделена так называемая остаточная часть системы.

Преобразование системы (14.1) в систему (3) выполнено с помощью ее первого уравнения, называемого разрешающим на данном шаге. Исключалась переменная 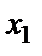, называемая разрешающей, коэффициент 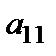при ней также называется разрешающим, столбец коэффициентов 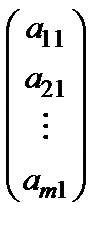при разрешающей переменной – разрешающим столбцом.

Если в системе (3) встретится уравнение вида 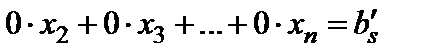, где 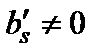, то система (14.1) несовместна. Если этого не произойдет, то, предполагая, что 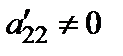, из всех уравнений остаточной части системы (3), кроме первого, исключим, аналогично предыдущему, неизвестную .

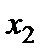Продолжая процесс преобразования остаточных частей получающихся систем, придем к одному из двух случаев:

1) либо в ходе преобразований получаем уравнение вида 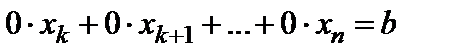, где 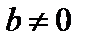, и тогда система (6.1) несовместна;

2) либо приходим к системе без остаточной части:

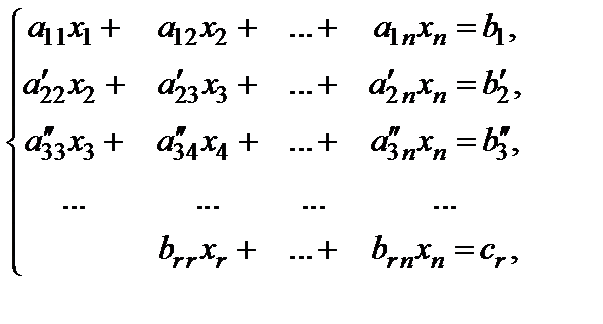(4)

где 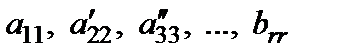отличны от нуля. Возможно уменьшение числауравнений по сравнению с исходной системой ( ). Это связано с тем, что в процессе преобразований вычеркиваются уравнения вида

.

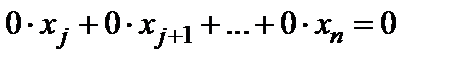Процесс преобразования системы (1) к системе (4) называют прямым ходом метода Гаусса.

Если в системе (4) 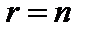, то она имеет треугольный вид. Из последнегоуравнения 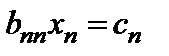находим 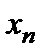_, из предпоследнего – 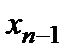и т.д. и, наконец, из первого – 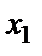,и, тем самым, – единственное решение системы (6.1). Описанный процесс называют обратным ходом метода Гаусса.

Если 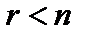, то в результате обратного хода, r неизвестных можно выразить линейно через остальные 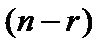неизвестных. Эти rнеизвестных называют базисными, а остальные 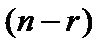– свободными. В результате получим общее решение системы в виде:

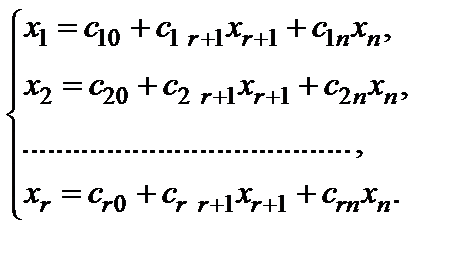(5)

Группу базисных неизвестных назовем базисом системы неизвестных. Общее решение (5) записано относительно базиса 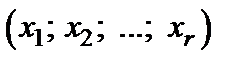. Ясно, что это решение можно записать относительно и других базисов, которых может быть не больше 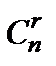(число сочетаний из п по r).

Чтобы получить какое-нибудь частное решение системы (14.1), нужно придать свободным неизвестным некоторые числовые значения. Ясно, что в случае r < п система (14.1) имеет бесконечное множество решений.